Ограниченная функция. Теорема об ограниченности функции.

Если функция f(x) имеет предел в точке a ,то она ограниченна

в некоторой окрестности точки a.

Теорема о произведении б.м функции на ограниченную

Произведение бесконечно малой при функции на ограниченную в

некоторой окрестности точки а функцию есть бесконечно малая функция при .

Теорема о делении б.м функции на функцию, предел которой отличен от 0.

Теорема о единственности предела функции. Теорема о существовании предела.

Теорема о существовании предела.Функция не может иметь более одного предела.

Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке. Если последовательность монотонно возрастает и ограниченна сверху, то она имеет предел.

Теорема сравнения.

в теории дифференциальных уравнений- теорема, утверждающая наличие определенного свойства решений дифференциального уравнения (или системы дифференциальных уравнений) в предположении, что некоторым свойством обладает вспомогательное уравнение или неравенство (система дифференциальных уравнении пли неравенств).

1) Теорема Ш т у р м а: любое нетривиальное решение уравнения обращается в нуль на отрезке [t0, t1] не более т раз если этим свойством обладает уравнение и при .

2) Дифференциальное неравенство: решение задачи покомпонентно неотрицательно при если этим свойством обладает решение задачи и выполнены неравенства

Предел суммы, произведения, частного.

1)Предел суммы двух функций равен сумме их пределов: 2)Предел произведения двух функций равен произведению их пределов:

3)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен :

Теорема о промежуточной функции

одна из простейших теорем, изучаемых в рамках курса математического анализа.

Пусть в некоторой окрестности точки функция заключена между двумя функциями и , имеющими одинаковый предел 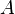при , то есть .

Тогда .

Доказательство. Из неравенства получаем неравенство . Условие позволяет предположить, что для любого существует окрестность , в которой верны неравенства и . Из изложенной выше оценки максимумом следует, что при , что удовлетворяет определению предела, то есть .

Первый замечательны предел.

При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел 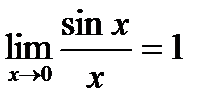называемый первым замечательным пределом.

Читается: предел отноешния синуса к его аргументу равен единице, когда аргумент стремится к нулю.

Доказательство:

Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. пусть 0<x< 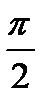. На рисунке 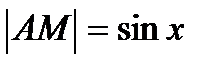, дуга МВ численно равна центральному углу х, 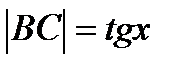. Очевидно, имеем 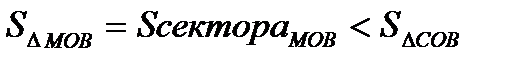. На основании соответствующих формул геометрии получаем 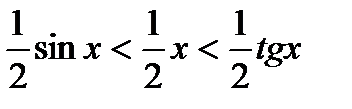. Разделим неравенство на 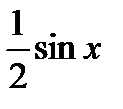>0, Получим 1<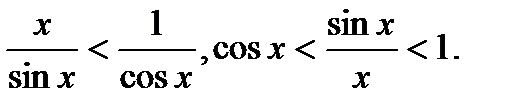

Так как 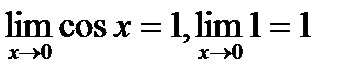, то по признаку ( о пределе промежуточной функции) существования пределов .

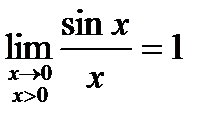А если x<0 => 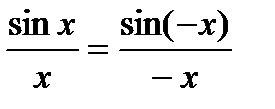, где –x>0 =>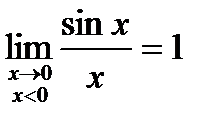

83. Второй замечательный предел.

Как известно, предел числовой последовательности 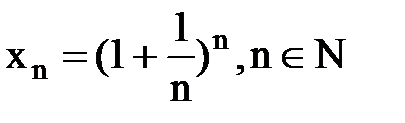, имеет предел равный e. 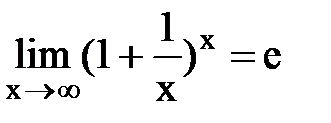. 1.Пусть 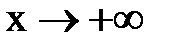. Каждое значение x заключено между двумя положительными целыми числами: 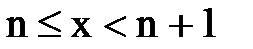, где n=[x] – это целая часть x. Отсюда следует 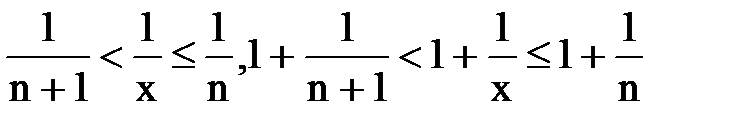, поэтому 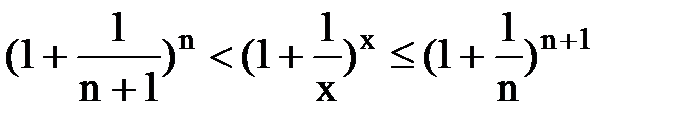. Если 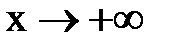, то . Поэтому: ,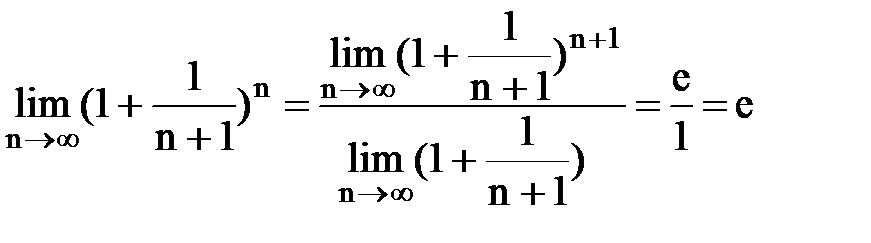

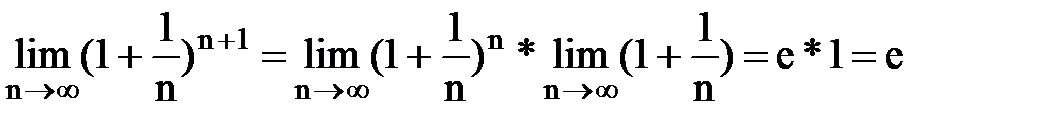. По признаку существования пределов: 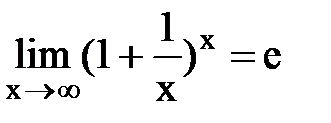. 2. Пусть 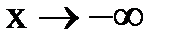. Сделаем подстановку –x=t, тогда 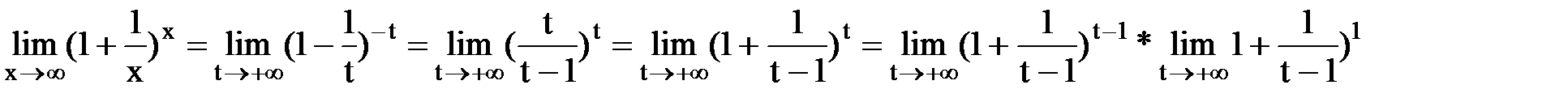= 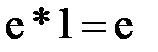. 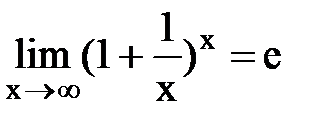и 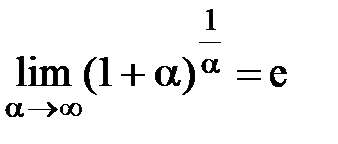называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция 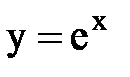называется экспоненциональной, употребляется также обозначение .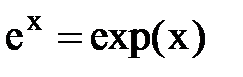