Число е. Натуральные логарифмы.

e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число eназывают числом Эйлера или числом Непера. Обозначается строчной латинской буквой «e».Натуральный логарифм — это логарифм по основанию e, где e — иррациональная константа, равная приблизительно 2,718281828. Натуральный логарифм обычно обозначают как ln(x), loge(x) или иногда просто log(x), если основание eподразумевается.

70. Конечный предел функции.

Предел (конечный и бесконечный) какой-либо подпоследовательности называется частичным пределом последней. Из всякой ограниченной последовательности можно выделить сходящуюсяподпоследовательность (теорема Больцано — Вейерштрасса), а из всякой неограниченной — бесконечно большую. В множестве всех частичных Предел последовательности всегда имеется как наибольший, так и наименьший (конечный или бесконечный). Наибольший (соответственно наименьший) частичный Пределпоследовательности x_n, n = 1, 2,..., называют её верхним (соответственно нижним) пределом и обозначается 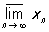(соответственно 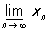). Например,

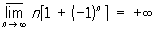
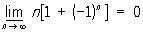
Последовательность имеет конечный или бесконечный Предел тогда и только тогда, когда её верхний Пределсовпадает с нижним, при этом их общее значение и является её Предел Конечный верхний Предел последовательности можно также определить как такое число а, что при любом e > 0 существует бесконечно много членов последовательности, больших, чем а — e, и лишь не более, чем конечное число членов, больших, чем a +e.

71. Бесконечный предел функции.

Условная запись 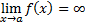обозначает, что для любого E > 0 справедливо неравенство:

|f(x)| > E, если только 0 < |x - a| < δ (E) .

72. Односторонние пределы.

число А называется пределом функции 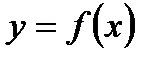слева в точке x₀, если для любого число 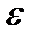>0 существует число 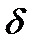= 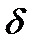( 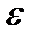)>0 такое, что при 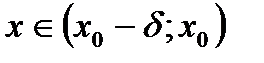выполняется неравенство .

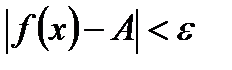Предел слева записывают так: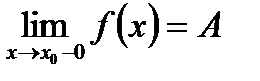

Аналогично определяется предел функции справа:

.

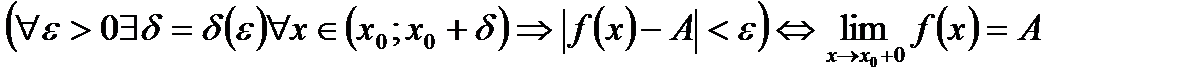Пределы функции слева и справа называются односторонними пределами.

73. Бесконечно малые и бесконечно большие функции. Связь между б.м и б.б функциями.

Функция 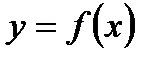называется бесконечно большойпри 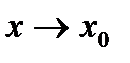,если для любого числа M>0 существует число 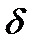= 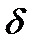(М)>0, что для всех х, удовлетворяющих неравенству 0< 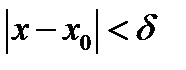, выполняется неравенство 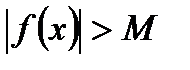. Записывают 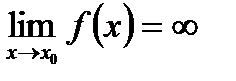. Коротко:

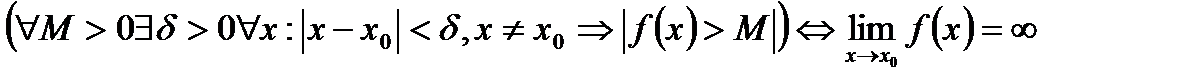
Функция 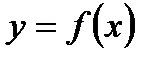называется бесконечно большойпри 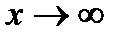,если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству 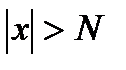, выполняется неравенство 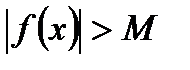. Коротко:

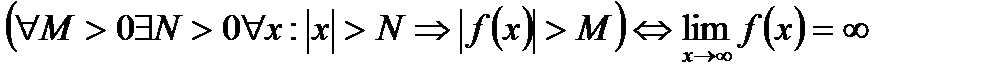
Всякая бесконечно большая функция в окрестности точки х0 является неограниченной в этой окрестности.

Бесконечно малая функция:
Функция 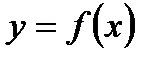называется бесконечно малой пр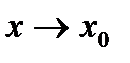и ,если 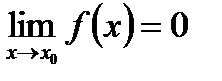: для любого числа 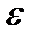>0 найдется число 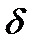>0 такое, что для всех х, удовлетворяющих неравенству 0< 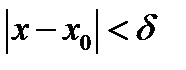, выполняется неравенство .

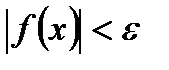Теорема: алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

Теорема: произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

Следствие: так как всякая б.м.ф. ограничена, то из теоремы вытекает произведение двух б.м.ф. есть функция бесконечно малая.

Следствие: произведение б.м.ф. на число есть функция бесконечно малая.

Теорема: частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.

Теорема: если функция - бесконечно малая, то обратная ей функция – бесконечно большая и наоборот.

74. Теорема о разности между функцией и её пределом.

Если функция 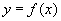имеет предел 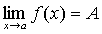, то разность между функцией и значением предела есть функция, бесконечно малая при .