Графическое представление вариационного ряда

Графическое представление результатов измерений выражается в построе­нии трех графиков: полигона частот (рис. 1), гистограммы (рис. 2) и полигона накопленных частот (кривой сумм или кумуляты) (рис. 4).

Полигон частот и гистограмма показывают распределение измеряемых показателей и их сгруппированность вокруг среднего значения.

Для построения полигоначастот в декартовых координатах по оси абсцисс откладываются срединные значения интервалов, а по оси ординат – соответст­вующие им частоты (или частости).

Рис. 1. Полигон частот результатов

Для построения гистограммы по оси абсцисс откладываются границы ин­тервалов и на них восстанавливаются прямоугольники до уровня частот, соответ­ствующих интервалам, отложенных по оси ординат (рис. 2).

Рис. 2. Гистограмма распределения результатов

Если нанести на гистограмму пунктирной линией полигон распределения частот, то мы получим первоначальное представление о дифференциальной функ­ции распределения.

Таким образом, теоретическим аналогом гистограммы является плот­ность распределения вероятностей, или дифференциальная функция распре­деления(рис. 3).

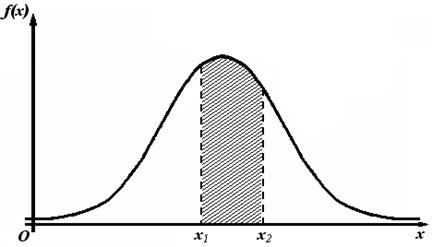
Рис. 3. Плотность распределения вероятностей

Иначе говоря, гистограмма является экспериментальным аналогом плотности распределения вероятностей.

Площадь гистограммы равна сумме всех частот, т. е. объёму выборки, или сумме частостей, т. е. единице.

Полигон накопленных частот показывает прирост показателей от интер­вала к интервалу, поэтому ее ещё называют кривой сумм или кумулятой. Для по­строения полигона накопленных частот по оси абсцисс откладываются верхние границы интервалов, а по оси ординат – соответствующие им накопленные час­тоты (или накопленные частости) (рис. 4).

накопленная

частота

Рис. 4. Полигон накопленных частот результатов

Теоретическим аналогом полигона накопленных частот результатов яв­ляется функция распределения, или интегральная функция распределения(рис. 5).

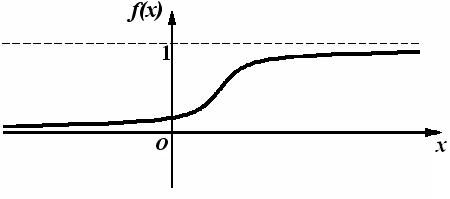
Рис. 5. Функция распределения

Иначе говоря, полигон накопленных частот результатов является экс­периментальным аналогом функции распределения.

Таким образом, графическое представление результатов измерений выяв­ляет закономерности их распределения и позволяет правильно выбрать последую­щие статистические характеристики для дальнейшего анализа полученных экспе­риментальных данных.

Однако прежде чем перейти к дальнейшим расчётам, напомним о нормаль­ном законе распределения.

Нормальное распределение

Большинство экспериментальных исследований не только в области физиче­ской культуры и спорта, но и в биологии, медицине и др. связано с измерениями, результаты которых могут принимать любые значения в заданном интервале, и описываются моделью непрерывных случайных величин, которые подчинены определённому закону распределения.

Среди всех непрерывных законов распределения вероятностей особое место занимает нормальное распределение, или распределение Гаусса, как наиболее часто встречающийся вид распределения.

Закон нормального распределения выражается следующей формулой:

,

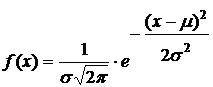где µ - математическое ожидание;

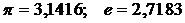(основание натурального логарифма);

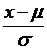- называется нормированным отклонением.

Поэтому этот закон называется законом нормального распределения, а гра­фик функции f(x) называют нормальной кривой, или кривой Гаусса (рис.6).

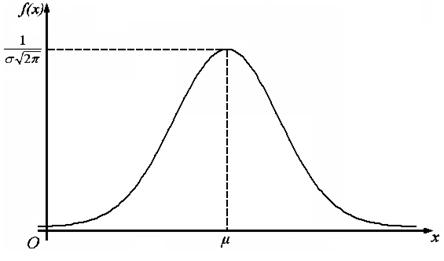
Рис. 6. Кривая нормального распределения

Теорема. Математическое ожидание случайной величины Х приближённо равно среднему арифметическому всех её значений (при достаточно большом числе испытаний).

Как видно из рисунка 6, график нормальной кривой представляет собой колоколообразную фигуру, симметричную относительно вертикальной прямой 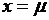, и асимптотически приближающуюся к оси абсцисс при .

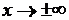Главная особенность нормального закона состоит в том, что он является пре­дельным законом, к которому приближаются другие законы распределения. При достаточно многочисленной совокупности нормальное распределение прояв­ляется и в эмпирическом распределении.

Определение. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей образует так называемое теоретическое распределение.

Определение.Совокупность фактических значений случайной величины, полученных в результате наблюдений, с соответствующими частотами (или частостями) образуют эмпирическое распределение.

Рассмотрим некоторые свойства нормального распределения.

1. График нормального распределения определен на всей оси ОХ, т. е. каж­дому значению х соответствует вполне определённое значение функции.

2. При всех значениях х (как положительных, так и отрицательных) функция принимает положительные значения, т. е. нормальная кривая расположена над осью ОХ.

3. Предел функции при неограниченном возрастании х равен нулю

.

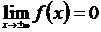Поскольку функция стремится к 0 при 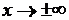, то ось абсцисс является асимптотой графика этой функции.

4. Функция в точке 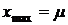имеет максимум, равный:

.

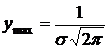5. График кривой f(x) симметричен относительно прямой, проходящей через точку х = μ.

Отсюда следует равенство для нормально распределённой величины моды, медианы и математического ожидания.

6. Коэффициенты асимметрии и эксцесса нормального распределения равны 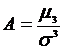0:

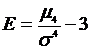= 0;

= 0.

Отсюда следует важность вычисления этих коэффициентов для эмпирических рядов распределения, т. к. они характеризуют скошенность и кру­тость данного ряда по сравнению с нормальным.

7. Изменение значений параметра 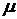(при неизменном 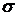) не влияет на форму нормальной кривой; кривая сдвигается вдоль оси Ox вправо, если 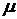возрас­тает, и влево, если 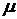убывает.

С изменением же значений параметра 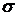форма нормальной кривой изменя­ется. Максимальная ордината графика функции убывает с возрастанием значения 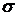(кривая «сжимается» к оси Ox) и возрастает с убыванием значения 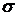(кривая «растягивается» в положительном направлении оси Oy).

На рис. 7. изображены три нормальные кривые при одном и том же значении 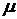и различных значениях .

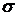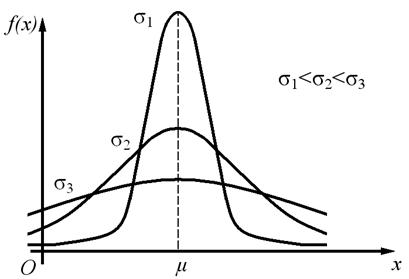
Рис. 7. Нормальные кривые при равных 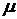и разных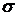

Аналитический анализ.