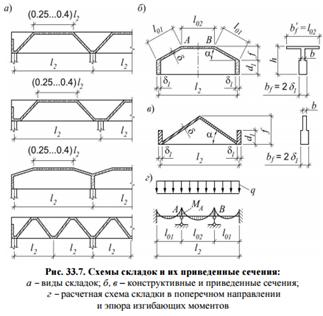
Вопрос №3. Усилия, действующие в оболочках и основные уравнения теории расчета тонких оболочек.

В качестве основы для расчета большинства применяемых в практике проектирования оболочек покрытий принята техническая теория расчета тонких оболочек. Согласно этой теории материал оболочки принимается упругим. Однако после образования трещин в бетоне растянутых зон проявляются неупругие деформации.

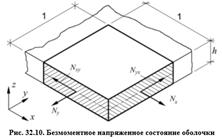
Напряженное состояние тонкостенной оболочки характеризуется внутренними усилиями, действующими в ее срединной поверхности, а также поперечными силами, изгибающими и крутящими моментами. Тонкостенные оболочки имеют значительно меньшую жесткость на изгиб в сравнении с жесткостью против действия сил, развивающихся в срединной плоскости. Поэтому, внешние нагрузки, действующие перпендикулярно срединной поверхности воспринимаются преимущественно нормальными (в плоскости) и сдвигающими усилиями. Следовательно, в большинстве оболочек, загруженных распределенными нагрузками по всей поверхности на значительной части возникает безмоментное напряженное состояние, А полное, т.е. моментное напряженное состояние возникает лишь в отдельных зонах оболочки – там, где происходит заметное искривление срединной поверхности, в местах приложения сосредоточенных нагрузок и резкого изменения толщины.

Безмоментное напряженное состояние оболочки достигается при соблюдении следующих основных условий:

• толщина оболочки много меньше других размеров;

• толщина оболочки изменятся плавно;

• внешняя распределенная по поверхности нагрузка изменяется плавно, без скачков;

• отсутствуют сосредоточенные нагрузки.

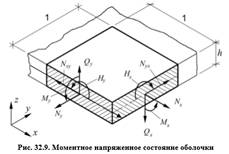Выделим из оболочки бесконечно малый элемент двумя парами сечений, параллельных осям «x» и «y» (рис. 32.9).

В общем случае в нормальных сечениях оболочек возникают нормальные силы Nx и Ny в плоскости оболочки, изгибающие моменты Mx и My, поперечные силы Qx и Qy, крутящие моменты Hy и Hx, сдвигающие силы Nxy и Nyx. В пологих оболочках можно принять 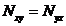и .

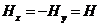Для безмоментного напряженного состояния 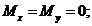. (рис. 32.10).

В последние годы интенсивно развиваются методы расчета тонкостенных пространственных покрытий, учитывающие геометрическую и физическую нелинейность, наличие трещин и перераспределение усилий и т.п. В их основе лежат численные методы (конечногоэлемента, конечных разностей). Реализация данных методов расчета осуществляется с применением компьютерных технологий.

Безмоментное напряженное состояние оболочки Для определения полной несущей способности оболочек при действии распределенных и сосредоточенных нагрузок можно использовать метод предельного равновесия. В нижеследующих лекциях приведены материалы по конструированию и определению несущей способности наиболее распространенных типов пространственных покрытий.

Вопрос №4. Цилиндрические оболочки и их конструктивные особенности.

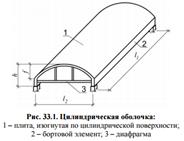
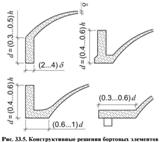Цилиндрическими называют оболочки, срединная поверхность которых очерчена в поперечном направлении по произвольной кривой, а в продольном имеет прямолинейные образующие. Цилиндрическая оболочка состоит из тонкой гладкой или ребристой плиты, изогнутой по цилиндрической пов-ти, сопряженной по криволинейным торцам с диафрагмами, а по продольным с бортовыми элементами. Диафрагмы обеспечивают геометрическую неизменяемость поперечного сечения оболочек. Нижние пояса диафр обычно выполняются с предварит напр А. L1-пролет оболочки, L2-длина волны, L1/L2≥1 - длинная оболочка, L1/L2≤1 - короткая. Оболочки м.б. однопролетными и многопрол, одноволновыми и многоволнов. h=(1/8...1/15)*L1, f=(1/5...1/10)*L2. Минимальная толщина монолитных оболочек 50мм, сборных 30мм. В необх случаях в верхн части могут устр фонарные отверст. По контуру отв устраив ребра жесткости. Диафр м.б. выполнены в виде: сплошных криволин балок, арок с затяжками, ферм с криволин верхним поясом. Бортовые элем являются опорой оболочки в направлнеиий пролета. В них размещ основная рабочая армат.

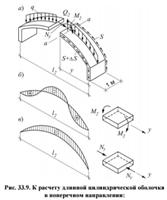Вопрос №5. Расчет длинных цилиндрических оболочек.

Изгиб момент в среднем сечении оболочки будет равен:

-для однопролетной одноволновой оболочки

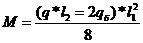
-для средней волны многоволновой оболочки

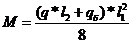
q-распред по поверхн нагр.

qб- собственный вес бортового элемента

Рассматривается условие равновесия

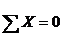
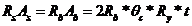
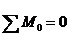
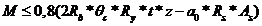
Ab-площадь попер сеч сжатой зоны бетона

0с-половина центрального угла, соотв границе сжатой зоны бетона оболочки

0,8 – опытный коэффициент условий работы;

t – толщина оболочки;

Ry – радиус кривизны круговой части сечения оболочки;

а0 –– расстояние от равнодействующей сил в растянутой арма- туре до центра кривизны круговой части сечения оболочки

z– расстояние от центра кривизны круговой части сечения обо- лочки до центра тяжести сжатой зоны бетона

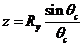
подставляемzивместоRsAs = 2Rb*0c*Ry*t, поделивна 1,6Rb*t*Ry^2, принявm=M/(1,6Rb*t*Ry^2) иn=a0/Ryполучим

sin0c-n*0c-m=0.

Оболочка может потерять н.с. от изгиб моментов действ в попер напр. Для опре данныз моментов (М2) из облочки двумя вертик плоскостями выделяется полоса шириной 1м. Это полоса находится в равновесии под действием внешней нагр qи сдвиг усилий S=тау*tи S+дельтаS.

Величины сдвигающих усилий опред по ф Журавского

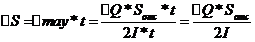При налич трещин по ф Лауля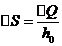

Q-приращение поперечных сил на участке оболочки длиной 1м

Sотс- статич момент отсеч части обол относит ц.т. сечения

I-момент инерции сечения обол.

h0-расст от равноденств усилий в арм бортов элем до края сжат зоны бетона.

Изгиб момент М2 в любом попер чес выделенной полосы обол ьудет равен сумме моментов всех сил, действ на элемент. 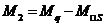,Mq-изгиб мом от внешн нагр и собств массы обол. Ms-изгиб мом от сдвиг сил относ рассм сечения.

Разруш обол может произойти от действия главных растяг усилий в угловых зонах констр. Для предотвр такого разруш по углам обол ставится А в напр действ главных растягив напр. Эта А рассчит на действ данных напр, велич кот около диафр м.б. принята равной сдвигающим усилиям.

Суммарное кол указанной арм устанавл в угловых зонах оболочки в количестве 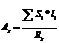Si-сдвигающее усилие на рассм уч длиной li.

Вопрос №6. Расчет складок.