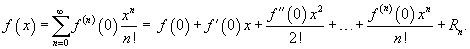Вариации произвольной постоянной
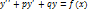
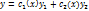
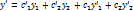
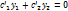
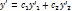
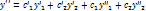
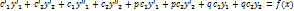
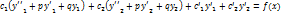
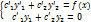
Пример.
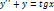
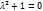
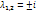
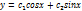
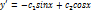
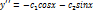
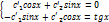
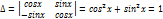
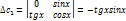
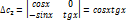
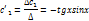
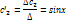
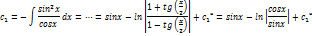
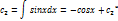
…
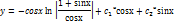
9) Методы решения неоднородурав-ния.В системе дифф уравнений метод исключения
Определения и методы решения

Определение 1.Уравнение вида:
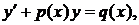 (1)
(1)
где 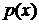 и
и 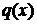 – заданные непрерывные функции на
– заданные непрерывные функции на 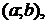 называется линейным дифференциальным уравнением (ЛДУ). Если
называется линейным дифференциальным уравнением (ЛДУ). Если 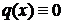 при
при 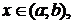 то уравнение имеет вид:
то уравнение имеет вид:
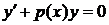
и называется линейным однородным дифференциальным уравнением (ЛОДУ). А если 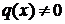 при
при 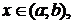 то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
Метод решения ЛНДУ
1) Метод вариации произвольной постоянной:
· сначала решить соответствующее ЛОДУ, которое является уравнением с разделяющимися переменными:
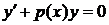
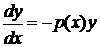
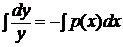
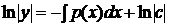
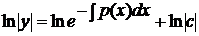
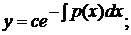 (2)
(2)
· заменить в формуле (2) постоянную 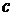 на неизвестную функцию
на неизвестную функцию 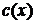 и подставить это выражение вместо
и подставить это выражение вместо 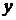 в уравнение (1), предварительно найдя
в уравнение (1), предварительно найдя 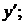
· из полученного уравнения найти функцию 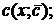
· записать ответ:
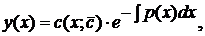
где 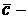 произвольная постоянная.
произвольная постоянная.
2) Метод Бернулли:
· выполнить в уравнении (1) замену Бернулли:
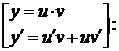
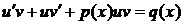
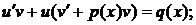 (3)
(3)
· приравнять к нулю выражение
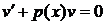
и найти отсюда любое частное решение 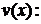
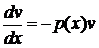
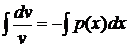
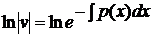
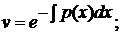
· подставить полученную функцию 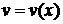 в уравнение (3) и найти общее решение
в уравнение (3) и найти общее решение 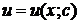 из этого уравнения;
из этого уравнения;
· записать ответ: 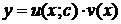
где 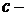 произвольная постоянная.
произвольная постоянная.
Уравнение Бернулли
Определение 2.Уравнение вида
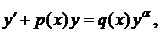 где
где 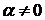 и
и 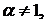 (4)
(4)
называется уравнением Бернулли с показателем 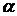 .
.
Уравнение (4) приводится к ЛНДУ(1) с помощью замены:
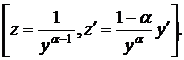
После этой замены уравнение (1) приводится к следующему:
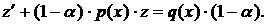
Это уравнение ЛНДУ относительно функции 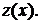 Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции
Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции 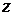 , решать методом замены Бернулли непосредственно. При этом функция
, решать методом замены Бернулли непосредственно. При этом функция 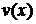 будет частным решением уравнения
будет частным решением уравнения
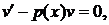
а функция 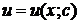 будет находиться из уравнения
будет находиться из уравнения
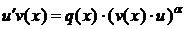 .
.
Замечание 1. При таком решении при 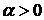 решение
решение 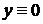 будет всегда потеряно.
будет всегда потеряно.
Замечание 2. Некоторые дифференциальные уравнения первого порядка становятся линейными или уравнениями Бернулли, если в них поменять ролями искомую функцию 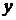 и независимую переменную
и независимую переменную 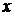 .
.
Неоднородная система дифференциальных уравнений, которая в большинстве случаев может встретиться вам в задачах, имеет следующий вид:
Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.
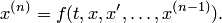
Введением новых функций
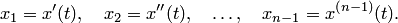
это уравнение заменяется нормальной системой 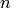 уравнений
уравнений
Можно утверждать и обратное, что, вообще говоря, нормальная система 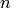 уравнений первого порядка
уравнений первого порядка
эквивалентна одному уравнению порядка 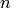 . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения.
. На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения.
Проиллюстрируем этот метод на примере системы двух уравнений:
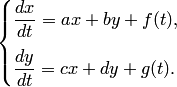
| (1) |
Здесь 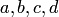 — постоянные коэффициенты, а
— постоянные коэффициенты, а 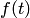 и
и 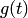 — заданные функции;
— заданные функции; 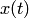 и
и 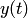 — искомые функции. Из первого уравнения системы (1) находим
— искомые функции. Из первого уравнения системы (1) находим
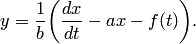
| (2) |
Подставляя во второе уравнение системы вместо у правую часть (2), а вместо 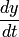 производную от правой части (2), получаем уравнение at второго порядка относительно
производную от правой части (2), получаем уравнение at второго порядка относительно 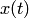
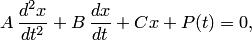
где 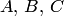 — постоянные. Отсюда находим
— постоянные. Отсюда находим 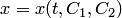 . Подставив найденное выражение для
. Подставив найденное выражение для 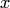 и
и 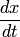 в (2), найдем
в (2), найдем 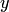 .
.
10. Числовые ряды. Опред сходимости числового ряда. Сумма, остаточный член числового ряда. Признаки сходимости: Признак Даламбера, радикальный и интегральный признаки сходимости Коши.
Числовой ряд – это сумма членов числовой последовательности вида 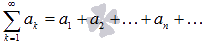 .
.
В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5: 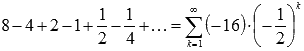 .
.
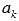 называют общим членом числового ряда или k–ым членом ряда.
называют общим членом числового ряда или k–ым членом ряда.
Для предыдущего примера общий член числового ряда имеет вид 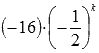 .
.
Частичная сумма числового ряда – это сумма вида 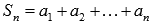 , где n – некоторое натуральное число.
, где n – некоторое натуральное число. 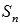 называют также n-ой частичной суммой числового ряда.
называют также n-ой частичной суммой числового ряда.
К примеру, четвертая частичная сумма ряда 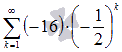 есть
есть 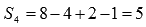 .
.
Частичные суммы 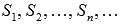 образуют бесконечную последовательность частичных сумм числового ряда.
образуют бесконечную последовательность частичных сумм числового ряда.
Для нашего ряда n –ая частичная сумма находится по формуле суммы первых n членов геометрической прогрессии 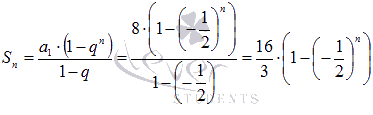 , то есть, будем иметь следующую последовательность частичных сумм:
, то есть, будем иметь следующую последовательность частичных сумм: 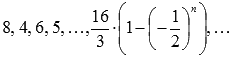 .
.
Числовой ряд 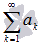 называется сходящимся, если существует конечный предел последовательности частичных сумм
называется сходящимся, если существует конечный предел последовательности частичных сумм 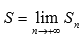 . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд
. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд 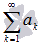 называется расходящимся.
называется расходящимся.
Суммой сходящегося числового ряда 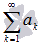 называется предел последовательности его частичных сумм, то есть,
называется предел последовательности его частичных сумм, то есть, 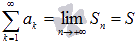 .
.
Признак Даламбера.
Пусть 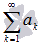 - знакоположительный числовой ряд. Если
- знакоположительный числовой ряд. Если 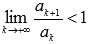 , то числовой ряд сходится, если
, то числовой ряд сходится, если 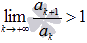 , то ряд расходится.
, то ряд расходится.
Замечание.
Признак Даламбера справедлив, если предел бесконечен, то есть, если 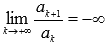 , то ряд сходится, если
, то ряд сходится, если 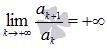 , то ряд расходится.
, то ряд расходится.
Если 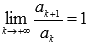 , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
, то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
Радикальный признак Коши.
Пусть 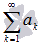 - знакоположительный числовой ряд. Если
- знакоположительный числовой ряд. Если 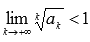 , то числовой ряд сходится, если
, то числовой ряд сходится, если 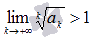 , то ряд расходится.
, то ряд расходится.
Замечание.
Радикальный признак Коши справедлив, если предел бесконечен, то есть, если 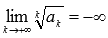 , то ряд сходится, если
, то ряд сходится, если 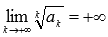 , то ряд расходится.
, то ряд расходится.
Если 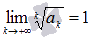 , то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
Обычно достаточно легко разглядеть случаи, когда лучше всего использовать радикальный признак Коши. Характерным является случай, когда общий член числового ряда представляет собой показательно степенное выражение.
Интегральный признак Коши.
Пусть 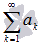 - знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции
- знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции 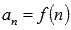 . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале
. Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале 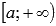 , где
, где 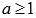 ). Тогда в случае сходимости несобственного интеграла
). Тогда в случае сходимости несобственного интеграла 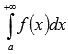 сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.
сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.
При проверке убывания функции y = f(x) на интервале 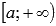 Вам может пригодится теория из раздела возрастание и убывание функции.
Вам может пригодится теория из раздела возрастание и убывание функции.
11. Функциональные ряды. Область сходимости функционального ряда. Степенные ряды. Теорема Абеля. Равенство сходимости методом Даламбера и Коши
Функциональный же ряд состоит из ФУНКЦИЙ:
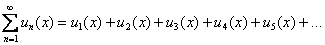
В общий член ряда 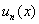 помимо многочленов, факториалов и других подарковнепременно входит буковка «икс». Выглядит это, например, так:
помимо многочленов, факториалов и других подарковнепременно входит буковка «икс». Выглядит это, например, так: 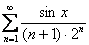 . Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
. Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
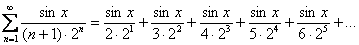
Как видите, все члены функционального ряда  – это функции.
– это функции.
Наиболее популярной разновидностью функционального ряда является степенной ряд.
Совокупность тех значений х при которых данный ряд сходится называется областью сходимости функционального ряда. Функциональный ряд сходится если, предел от остаточного члена ряда при n->∞равен 0.
Степенной ряд – это ряд, в общий член  которого входят целые положительные степени независимой переменной
которого входят целые положительные степени независимой переменной 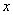 . Упрощенно степенной ряд во многих учебниках записывают так:
. Упрощенно степенной ряд во многих учебниках записывают так: 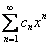 , где
, где 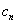 – это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:
– это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:
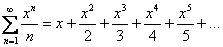
Теорема Н. Абеля.
Если степенной ряд 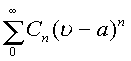 сходится в точке
сходится в точке 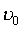 , то он сходится и в любой точке
, то он сходится и в любой точке 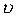 , расположенной ближе к центру
, расположенной ближе к центру 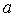 , чем
, чем 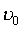 , причем в любой сфере
, причем в любой сфере 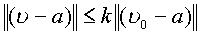 , где
, где 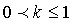 , сходимость ряда равномерна.
, сходимость ряда равномерна.
12. Ряды Тейлора и Макларена. Разложение элементарных функций в ряд Макларена
Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:
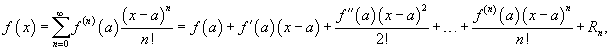
где Rn − остаточный член в форме Лагранжа определяется выражением
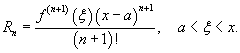
Если приведенное разложение сходится в некотором интервале x, т.е. 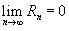 , то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.
Если a = 0, то такое разложение называется рядом Маклорена: