Определите понятие однородной функции порядка n. Записать однородное дифференциальное уравнение первого порядка и объяснить способ его решения.

41.Функция ƒ(x;y) называется однородной функцией N-го поpядкa (измерения), если при умножении каждого ее аргумента на произвольный множитель λ вся функция умножится на A^N, т. е. F(λ*x; λ*y)= λⁿ*f(x;y).

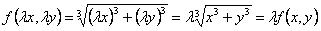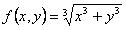^{= - однородная функция} первого порядка

Линейное дифференциальное неоднородное уравнение I-го порядка с произвольными коэффициентами имеет общий вид:

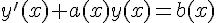
Однородные дифференциальные уравнения первого порядка. Дифференциальное уравнение первого порядка:

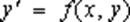
БИЛЕТ

Записать линейное однородное и неоднородное дифференциальное уравнения первого порядка. Изложить решение линейного ДУ-1 по методу Бернулли.

Обыкновенное дифференциальное уравнение вида: 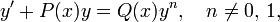называется уравнением Бернулли (при n = 0 или n = 1 получаем неоднородное или однородное линейное уравнение).

Способ решения:

^{Заменим 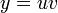, тогда 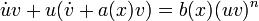. Подберем 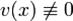так, чтобы было 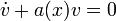. Для этого достаточно решить уравнение с разделяющимися переменными 1-го порядка. После этого для определения U получаем уравнение 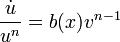-- уравнение с разделяющимися переменными}.

БИЛЕТ

Перечислите виды интегрируемых ДУ-2. Сформулировать задачу Коши для ДУ-2. Изложите способ решения простейших дифференциальных уравнений высших порядков, методом понижения порядка дифференциального уравнения.

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений. Состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям.
Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием. Этим мотивируется терминология и выбор обозначений: начальные данные задаются при t = 0, а решение отыскивается при t > 0.
задача Коши имеет единственное решение, если она имеет решение y = f(x) и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки (x0,y0) имеет поле направлений, совпадающее с полем направлений y = f(x). Точка (x0,y0) задаёт начальные условия.
задачей Коши для уравнения n–го порядка
y(n) = f (x, y, y ', ..., y(n - 1) )
называется задача отыскания решения y = y(x), удовлетворяющего начальным условиям

Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Рассмотрим случаи, когда возможно понижение порядка.
Уравнения вида y(n) = f(x). Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

БИЛЕТ

Дать определение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами. Изложить правило составления характеристического уравнения. Объяснить способ записи его решения в зависимости от корней характеристического уравнения.

Дифференциальное уравнение второго порядка имеет вид F(x,y,y',y")=0.
Линейным однородным уравнением второго порядка называется уравнение y"+p(x)y'+q(x)y=0.
Если коэффициенты p(x) и q(x) постоянны, т.е. не зависят от x , то это уравнение называют уравнением с постоянными коэффициентами и записывают его так: y''+py'+qy=0.

Для получения из линейного однородного уравнения характеристического уравнения необходимо заменить функции y единицей, а y' и y" соответствующими степенями k

БИЛЕТ