Дифференциальные уравнения. Задача Коши

Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Дифференциальное уравнение с разделяющимися переменными

В качестве дифференциальных уравнений с разделяющимися переменными принято определять ОДУ первого порядка, приводящиеся к виду 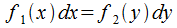(ДУ с разделенными переменными).

Запишем такие уравнения:

а)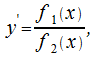

б)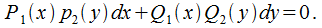

Линейное ДУ первого порядка

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

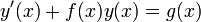
Формулы комбинаторики

· Размещение:

Размещение из n по m элементам называется любая упорядоченная выборка содержащая m-элементов.

Любые 2 размещения считаются различными, если они отличаются друг от друга составом или порядком следования элементов.

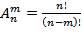
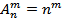
· Перестановка:

Перестановкой из n-элементов называется размещение из n по m.

2 любые перестановки отличаются только порядком следования элементов.

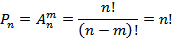
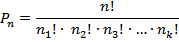
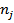- количество повторений j-ого элемента.

· Сочетание:

Сочетание из n-элементов по m-элементам называется любое подмножество одного множества. Два любых элемента отличаются друг от друга хотя бы элементом.

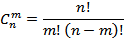
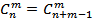
Случайные события. Операции со случайными событиями

Опр. Событие, которое при одних и тех же условиях может наступить, либо не наступить называется случайным событием A,B,C.

Операции со случайными событиями:

Число А называется подсобытие события В, если из наступления события А следует наступление события В.

Противоположным событием вектора А к событию А называется событие заключающейся в том, что событие А не наступает.

Опр. Если А является пособытием события В, то А благоприятно для В.

Опр.Сумма двух случайных событий А+В называется событие С, которое состоит в том, что наступает или событие А, или В, или оба вместе.

А+В=С

Опр.Произведением А*В называется заключающееся в том, что наступает и событие А и событие В одновременно.

Опр.Если А*В= 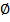есть событие невозможное, то такие события называются не совместными.

Классическое определение вероятности

Классическое определение вероятности

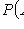
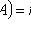
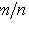
(m - число благоприятных исходов опыта; n - число всех его исходов)

Под вероятностью случайного события понимают, некоторую объективную характеристику того, на сколько часто это событие может наступать.

Свойства вероятностей событий

·

·

·

·

·

·

·

·

·

·

·

·

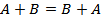
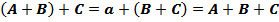
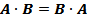
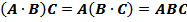
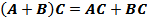
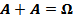
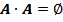
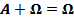
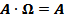
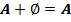
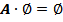
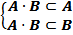
Опр.Н₁, Н₂…Н_n – образуют полную группу событий, если они удовлетворяют двум свойствам:

1.

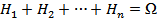
2.