Признаки постоянства и монотонности функции.

Признаки постоянства и монотонности функции.

1) для того, чтобы функция была постоянной на интервале ав необходимо и достаточно, чтобы в каждой точке этого интервала функция была производной и ровна 0.

2) Для того, чтобы функция f(x) возростала на интервале ав необходимо и достаточно, чтобы функция f(x) была больше 0

3) Для того, чтобы функция f(x) убывала, на интервале ав необходимо и достаточно, чтобы функция f(x) была меньше 0

4) Пусть f(x) дифференцируема на интервале ав и точка с находится внутри этого интервала, тогда если функция в точке с принимает наибольшее или наименьшее значение, то f΄(с)=0

14. Признаки экстремума функции.

Точка х0- точка локального максимума ( минимума) ф-ции f(x), если существует такая окрестность в точке х0 ( х0-Е, х0+Е), что ( f(x0)>f(x); Vx принадлежит (x0эпсилент, х+эпсилент) для всякого х для данной окрестности.

Точка локального минимума и максимума- точка экстремума. Пусть f(x)- дифференциальна на интервале ав, точка с лежит внутри этого интервала. Для того, чтобы точка с была точкой экстремума необходимо, чтобы f(x)=0. это условие необходимое и достаточное.

Теорема:

Пусть функция f(x) определена на всем интервале ав и деференциальна во всех точках этого интеграла за исключением может быть точки с. Тогда для того чтобы точка с была точкой экстремума, достаточно, чтобы производная меняла знак при переходе через точку с. При чем точка с будет точкой максимума, если знак меняется с плюса на минус, и точкой минимума, если знак меняется с минуса на плюс.

Признак выпуклости функции.

Говорят, что функция на интервале ав выпукла вверх (вниз), если ее график лежит выше (ниже) касательной графиков в любой точке этого интервала.

Точка на график ф-ции, в которой выпуклость вверх переходит в выпуклость вниз или наоборот называется точкой перегиба графикаю

Теорема: пусть функция y=f(x) дважды дифференцирована на интервале ав. Для того, чтобы ф-ця f(x0 на интервале ав была выпукла вверх ( вниз), необходимо и достаточно, чтобы f’’(x)≤0, (f”’(x)≥0)

Асимптоты графика функции.

Асимптотой графика функции называется прямая расстояние от которой до точки на графике функции стремится к 0, при бесконечном удалении точки на графике от начла координат.

Асимптоты бывают: горизонтальные, вертикальные и наклонные.

Вертикальная асимптота: х=а, где а- точка бесконечного графика ( разрыв второго рода)

Наклонные асимптоты: у=kx+b, где k- определяется из условия k=limx-±∞(f(x)-k(x))

17. Первообразная. Неопределенный интеграл. Свойства неопределенного интеграла.

Пусть ф-ция f(x) непрерывна на интервале ав, ф-ция F(x) называется первообразной для ф-ции f(x), если выполняется равенство: F’(x)=f(x)

Ясно, что если с- любое число ( постоянная величина), то F(x)+c- так же будет первообразная для f(x) (F(x)+C)’=F’(x)+C’=f(x) т.е. если ф-ция f(x) существует хотя бы 1 первообразную, то их будет бесконечное множество и все они будут отличаться друг от друга на некоторое число С.

Пусть ф-ция f(x) непрерывна на интервале ав, тогда совокупность всех первообразных для нее называется неопределенным интегралом и обозначается: ⌠f(x)dx=F(x)+C

Вычисление неопределенного интеграла называется интегрированием.

Свойства неопределенного интеграла:

1) ⌠f(x)dx=⌠dF(x)=F(x)+C

2) (⌠f(xdx)’=(F(x)+C)’=f(x)

3) ⌠(f(x)+g(x))dx=⌠f(x)dx+⌠g(x)dx

4) ⌠λf(x)dx=λ⌠f(x)dx+⌠g(x)dx

Замена переменной в неопределенном интеграле.

Производится с помощью подстановок 2-х видов:

1) подведение ф-ции под знак дифференциала

2) замена переменной

идея метода замены переменной состоит в том, чтобы сложное выражение ( или не которую ф-цию) замеить одной буквой.

5) Замена переменной в неопределенном интеграле

⌠f(x)dx

X=φ(t) (α,β)

Некоторая дифференцированная ф-ция на интервале, тогдп справедливо равенство: ⌠f(x)dx=⌠f(φ(t))*φ’(t)dt

Интегрирование по частям в неопределенном интеграле.

Пусть ф-ция u(x); v(x) дифференцируема на интервале ав и существует интеграл: ⌠u’(x)v(x)dx, тогда существует интеграл ⌠u(x)v(x)dx=u(x)v(x)- ⌠u’(x)v(x)dx- формула интегрирования по частям.

f(x)dx=df(x)

⌠udv=uv-⌠vdu

Свойства определенного интеграла

1)а

⌠f(x0dx=0

b

2) a a

⌠f(x)dx=-⌠f(x)dx

b b

3) b b b

⌠(f(x)+g(x))dx=⌠f(x)dx+⌠g(x)dx

a a a

4)a a

⌠αf(x)dx=α⌠f(x)dx

b b

5)a c b

⌠f(x)dx=⌠f(x)dx+⌠f(x)dx

b a c b

6)m≤f(x)≤M: любое х принадлежит отрезку ав. m(b-a)≤ ⌠f(x)dx≤M(b-a)

A

7)f(x)непрерывна на отрезке ав, (то)=>существует с принадлежащая отрезку ав

b

⌠f(x)dx=f(c)*(b-a)

A

Формула Ньютона-Лейбница

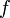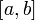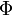Если непрерывна на отрезке и — ее любая первообразная на этом отрезке, то имеет место равенство

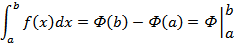
Линейное ДУ первого порядка

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

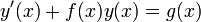
Формулы комбинаторики

· Размещение:

Размещение из n по m элементам называется любая упорядоченная выборка содержащая m-элементов.

Любые 2 размещения считаются различными, если они отличаются друг от друга составом или порядком следования элементов.

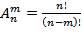
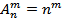
· Перестановка:

Перестановкой из n-элементов называется размещение из n по m.

2 любые перестановки отличаются только порядком следования элементов.

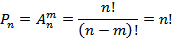
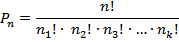
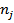- количество повторений j-ого элемента.

· Сочетание:

Сочетание из n-элементов по m-элементам называется любое подмножество одного множества. Два любых элемента отличаются друг от друга хотя бы элементом.

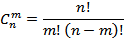
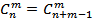
Формула полной вероятности

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) B₁, В₂,...,В_n, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

Р(А) = Р (В₁) Р_В1(А) + Р (В₂) Р_В2(А) + ... + Р (В_n) Р_Вn(А). (*)

где Р(В₁)+Р(В₂)+...+Р(В_n)=1.

Формула Байеса

,

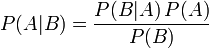где

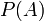— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

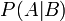— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

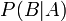— вероятность наступления события B при истинности гипотезы A;

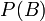— полная вероятность наступления события B.

Формула Бернулли

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность 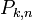того, что событие A наступит k раз в n независимых испытаниях, равна: 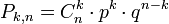, где .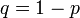

Дискретные случайные величины. Таблица распределения

ОПРЕДЕЛЕНИЕ. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

X	x1	x2	...	xn
P	p1	p2	...	pn

Признаки постоянства и монотонности функции.

1) для того, чтобы функция была постоянной на интервале ав необходимо и достаточно, чтобы в каждой точке этого интервала функция была производной и ровна 0.

2) Для того, чтобы функция f(x) возростала на интервале ав необходимо и достаточно, чтобы функция f(x) была больше 0

3) Для того, чтобы функция f(x) убывала, на интервале ав необходимо и достаточно, чтобы функция f(x) была меньше 0

4) Пусть f(x) дифференцируема на интервале ав и точка с находится внутри этого интервала, тогда если функция в точке с принимает наибольшее или наименьшее значение, то f΄(с)=0

14. Признаки экстремума функции.

Точка х0- точка локального максимума ( минимума) ф-ции f(x), если существует такая окрестность в точке х0 ( х0-Е, х0+Е), что ( f(x0)>f(x); Vx принадлежит (x0эпсилент, х+эпсилент) для всякого х для данной окрестности.

Точка локального минимума и максимума- точка экстремума. Пусть f(x)- дифференциальна на интервале ав, точка с лежит внутри этого интервала. Для того, чтобы точка с была точкой экстремума необходимо, чтобы f(x)=0. это условие необходимое и достаточное.

Теорема:

Пусть функция f(x) определена на всем интервале ав и деференциальна во всех точках этого интеграла за исключением может быть точки с. Тогда для того чтобы точка с была точкой экстремума, достаточно, чтобы производная меняла знак при переходе через точку с. При чем точка с будет точкой максимума, если знак меняется с плюса на минус, и точкой минимума, если знак меняется с минуса на плюс.

Признак выпуклости функции.

Говорят, что функция на интервале ав выпукла вверх (вниз), если ее график лежит выше (ниже) касательной графиков в любой точке этого интервала.

Точка на график ф-ции, в которой выпуклость вверх переходит в выпуклость вниз или наоборот называется точкой перегиба графикаю

Теорема: пусть функция y=f(x) дважды дифференцирована на интервале ав. Для того, чтобы ф-ця f(x0 на интервале ав была выпукла вверх ( вниз), необходимо и достаточно, чтобы f’’(x)≤0, (f”’(x)≥0)

Асимптоты графика функции.

Асимптотой графика функции называется прямая расстояние от которой до точки на графике функции стремится к 0, при бесконечном удалении точки на графике от начла координат.

Асимптоты бывают: горизонтальные, вертикальные и наклонные.

Вертикальная асимптота: х=а, где а- точка бесконечного графика ( разрыв второго рода)

Наклонные асимптоты: у=kx+b, где k- определяется из условия k=limx-±∞(f(x)-k(x))

17. Первообразная. Неопределенный интеграл. Свойства неопределенного интеграла.

Пусть ф-ция f(x) непрерывна на интервале ав, ф-ция F(x) называется первообразной для ф-ции f(x), если выполняется равенство: F’(x)=f(x)

Ясно, что если с- любое число ( постоянная величина), то F(x)+c- так же будет первообразная для f(x) (F(x)+C)’=F’(x)+C’=f(x) т.е. если ф-ция f(x) существует хотя бы 1 первообразную, то их будет бесконечное множество и все они будут отличаться друг от друга на некоторое число С.

Пусть ф-ция f(x) непрерывна на интервале ав, тогда совокупность всех первообразных для нее называется неопределенным интегралом и обозначается: ⌠f(x)dx=F(x)+C

Вычисление неопределенного интеграла называется интегрированием.

Свойства неопределенного интеграла:

1) ⌠f(x)dx=⌠dF(x)=F(x)+C

2) (⌠f(xdx)’=(F(x)+C)’=f(x)

3) ⌠(f(x)+g(x))dx=⌠f(x)dx+⌠g(x)dx

4) ⌠λf(x)dx=λ⌠f(x)dx+⌠g(x)dx