Ранг матрицы. Способы его нахождения.

Рассмотрим прямоугольную матрицу

Выделим в этой матрице k произвольных строк и k произвольных столбцов (k≤n, k≤m). Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы. Так, у матрицы с тремя строками и пятью столбцами возможны миноры первого, второго и третьего порядка.

Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы :

- замены строк столбцами, а столбцов соответствующими строками;

- перестановки строк матрицы;

- вычеркивания строки, все элементы которой равны нулю;

- умножения строки на число, отличное от нуля;

- прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число.

Подчеркнем, что сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.

Пример 1. Определить ранг матрицы

Решение

Все миноры второго и третьего порядков данной матрицы равны нулю, т.к. элементы строк этих миноров пропорциональны. Миноры первого порядка (сами элементы матрицы) отличны от нуля. Следовательно, ранг матрицы равен единице.

Пример 2. Определить ранг матрицы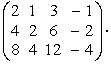

Решение

Вычеркнув из этой матрицы вторую строку и выбрав первый и четвертый столбцы, получим минор

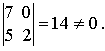
Ранг матрицы равен 2.

Решение линейных систем уравнений методом Крамера, Гаусса, матричным методом.

Метод Крамера

Для системы n линейных уравнений с n неизвестными (над произвольным полем)

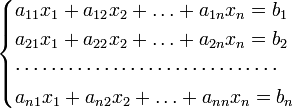
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде

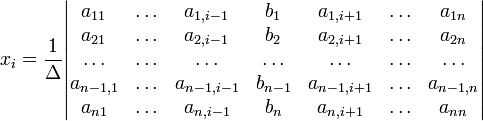
(i-ый столбец матрицы системы заменяется столбцом свободных членов).

В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:

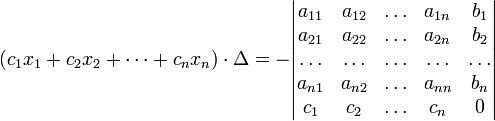
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца(определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы b1,b2,...,bn и x1,x2,...,xn, либо набор c1,c2,...,cn состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.

Пример

Система линейных уравнений:

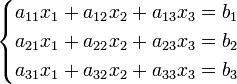
Определители:

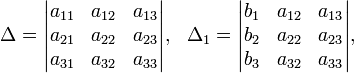
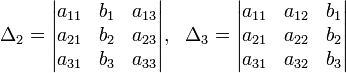
Решение:

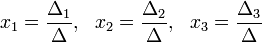
Пример:

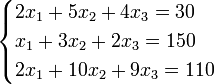
Определители:

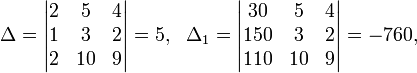
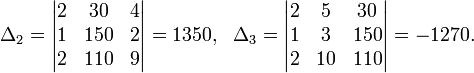
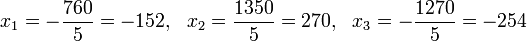
Метод Гаусса

Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно - предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:
- перестановка местами двух уравнений;
- умножение обеих частей одного из уравнений на любое число, отличное от нуля;
- прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.

Пример 1. Решить систему 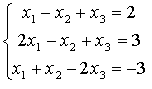методом Гаусса.

Решение

Определитель системы не равен нулю (см. пример из 2.2.1). Поэтому система совместна и определена (решение единственно). Выполним преобразования.

Первое уравнение оставим без изменения. Для того, чтобы избавиться от первого неизвестного во втором и третьем уравнениях, к ним прибавим первое, умноженное на -2 в первом случае и на -1 - во втором

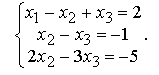
Теперь избавимся от второго неизвестного в третьем уравнении. Для этого второе уравнение умножим на -2 и прибавим к третьему. Получим эквивалентную заданной систему треугольного вида

Решаем систему снизу вверх. Из третьего уравнения имеем x3= 3 и, подставляя его во второе уравнение, находим x2= 2. Поставив найденные неизвестные в первое уравнение, получим x1= 1. Таким образом, получим решение системы: x1= 1, x2= 2, x3= 3.

Проверка: 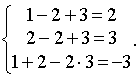Получили три тождества.

Пример 2. Решить систему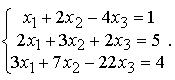

Решение

В ней 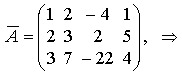для исключения первого неизвестного во второй и третьей строках (уравнениях) умножим первую строку расширенной матрицы на -2 и -3 и сложим полученные результаты со второй и третьей строками соответственно.

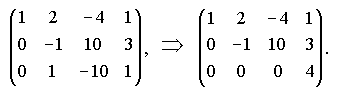
Следовательно, мы пришли к эквивалентной системе

Ее третье уравнение получено в результате сложения двух последних уравнений (строк).

Найдя 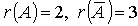, мы приходим к выводу, что система несовместна. Об этом же говорит и противоречие в третьем уравнении системы.

Пример 2. Решить систему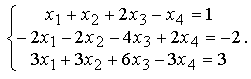

Решение

В ней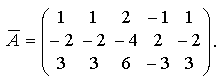

Умножим первую строку расширенной матрицы на 2 и -3, сложим полученные результаты со второй и третьей строками соответственно и получим

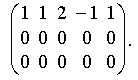
Следовательно, мы пришли к эквивалентной системе

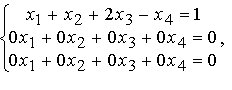
которая может быть представлена в виде

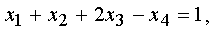
поскольку два последних уравнения - истинные равенства.

Поскольку 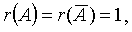постольку система совместна, но имеет множество решений. Общее решение системы имеет вид

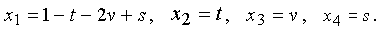
Множество частных решений системы будет трехмерным, так как зависит от трех параметров. Выбрав t = 2, v = 1, s = -3, получим частное решение системы x1 = - 6, x2 = 2, x3 = 1, x4= -3.

Матричный метод

Матричным методом могут быть решены только те системы, у которых число уравнений совпадает с числом неизвестных и определитель матрицы коэффициентов отличен от нуля (матрица А невырожденная).

Из этих условий следует, что 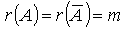и, следовательно, система совместна и определена.

Решение системы можно получить так: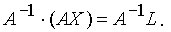

Используя свойства произведения матриц и свойство обратной матрицы

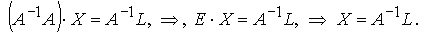
Т.е., для получения столбца неизвестных нужно обратную матрицу матрицы коэффициентов системы умножить на столбец свободных членов.

Пример Решить систему 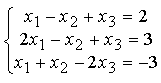матричным методом.

Решение

В соответствии с пунктом 1.5 найдем обратную матрицу для матрицы коэффициентов системы

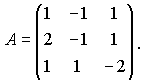
Вычислим определитель, раскладывая по первой строке:

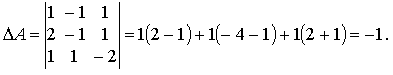
Поскольку Δ ≠ 0, то A-1 существует.

Обратная матрица найдена верно.

Найдем решение системы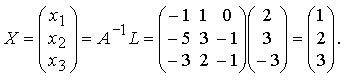

Следовательно, x1 = 1, x2 = 2, x3 = 3.

Проверка: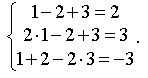

Система решена верно.

Матричный метод годится для решения любых систем, у которых матрица А квадратная и невырожденная.