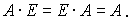Матрицы. Операции над матрицами. Их свойства.

Прямоугольной матрицей размерностью n на m называется прямоугольная таблица, состоящая из n строк и m столбцов.

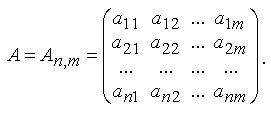
Величины, из которых состоит эта таблица, называются элементами матрицы и обозначаются той же буквой, только строчной, что и матрица, с указанием номера строки (первый индекс) и номера столбца (второй индекс).

Если число строк равно числу столбцов, то матрицу называют квадратной порядка, равного числу строк (столбцов).

Например, 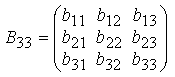- квадратная матрица третьего порядка.

Элементы квадратной матрицы, имеющие одинаковые первый и второй индекс (b11 b22b33), образуют главную диагональ. Элементы b11 b22 b33 этой матрицы образуют побочную диагональ. Квадратная матрица, независимо от ее порядка, называется единичной матрицей, если элементы ее главной диагонали равны единице, а все остальные элементы равны нулю. Такую матрицу обозначают Е.

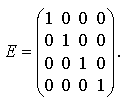
Если матрица состоит только из одной строки (столбца), то она называется матрицей-строкой (матрицей-столбцом).

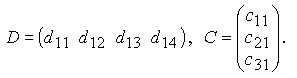
Как и у чисел, у матриц существует матрица, выполняющая роль нуля, - нулевая матрица. Это матрица, все элементы которой равны нулю.

Две матрицы считаются равными, если размеры матриц (число строк и столбцов) одинаковы и равны элементы, лежащие на пересечении соответствующих строк и столбцов.

В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число.

Пример.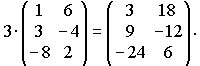

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число.

Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

Складывать и вычитать можно только матрицы одинаковой размерности.

Суммой (разностью) двух матриц называется матрица той же размерности, что и исходные, каждый элемент которой определяется как сумма (разность) соответствующих элементов матриц.

Пример.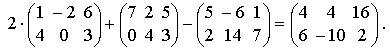

Очевидно, результат сложения не изменится, если слагаемые матрицы поменять местами.

Если к матрице прибавить или от нее отнять нулевую матрицу той же размерности, то получим исходную матрицу.

Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя.

Пример.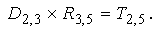

Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата

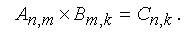
Элемент ci,j матрицы – ответа принадлежащий i-ой строке и j-му столбцу, вычисляется как произведение i-ой строки первого сомножителя An,m на j-ый столбец второго сомножителяBm,k. Так, например, при вычислении элемента умножается первая строка на третий столбец, а при вычислении элемента умножается третья строка на первый столбец.

Можно перемножать только те строки и столбцы, у которых одинаковое число элементов (смотри условие возможности умножения матриц). В результате получается число, равное сумме произведений соответствующих элементов (первый элемент строки на первый элемент столбца плюс второй элемент строки на второй элемент столбца и т. д. и, наконец, плюс произведение последних элементов).

Рассмотрим умножение матриц на примере :

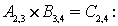
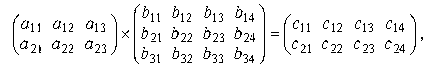
где

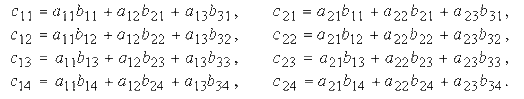
Пример.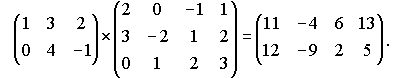

Пусть имеем матрицу А.

Матрицей, обратной матрице А, называется матрица A-1 такая, что A-1A = A A-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠0 ). Это условие является и достаточным для существования A-1матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.
1. Находим определитель матрицы. Если Δ ≠0, то матрица A-1 существует.
2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i - ой строки и j - го столбца будет алгебраическое дополнение Aij (см. 1.3.) элемента aij исходной матрицы.
3. Транспонируем матрицу В и получим BT.

Транспонировать матрицу - это значит поменять строки и столбцы местами (первый столбец с первой строкой, второй столбец со второй строкой и т. д.).
4. Найдем обратную матрицу

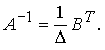
После вычисления обратной матрицы рекомендуется убедиться в том, что выполняется одна из частей условия.

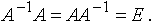
Пример Найдем обратную матрицу для матрицы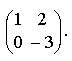

Решение

Вычисления произведем в соответствии с описанной схемой.
1.
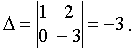
2.
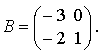
3.
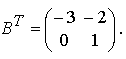
4.
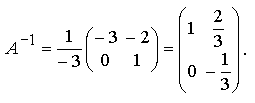
5.

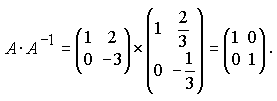
Обратная матрица найдена верно.

Отметим основные свойства операции произведения матриц.

1) В общем случае 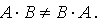. Если 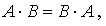то матрицы А и Вназываются перестановочными по отношению друг к другу.

2)

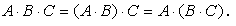
3)

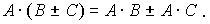
4) При умножении любой квадратной матрицы на единичную первоначальная матрица не меняется