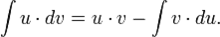Правило дифференцирования сложной функции.

y=f(u); y'=f'(u)*u'

1. Первообразная и неопределенный интеграл. Основные свойства.

Операция, обратная дифференцированию.

f(x) = F'(x)

(x^2)' = 2x

Операция нахождения функции F(x) по заданной функции f(x) называется интегрированием, а сама функция f(x) первообразной.

dF(x)/dx = f(x) => dF(x) = f(x)dx

dF(x) = f(x)dx

d(F(x)+C)/dx = fx

Две первообразные могут отличаться только на величину константы.

Совокупность всех первообразных функций f(x) называют неопределенным интегралом, а операция интегрирования обозначают:

∫f(x)dx = F(x) + C

f(x) — подынтегральная функция.

Х — переменная интегрирования.

Если функция f(x) непрерывна на отрезке от А до В, то она имеет первообразную на том отрезке, а значит и неопределенный интеграл.

Свойства:

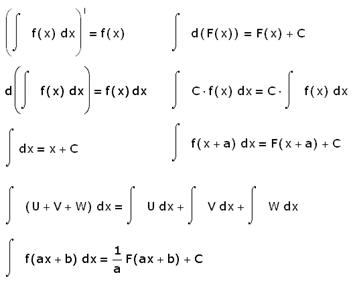
1. Область определения функции.

1) Если в функции есть корень чётной степени, то подкорное выражение должно быть больше нуля.
2) Если в функции есть дробь, то её знаменатель не должен быть равен нулю.
3) Если в функции содержится выражение f(x) в степени g(x), то f(x) больше, либо равна нулю, причём f(x) и g(x) одновременно не равны нулю.
4) Если в функции имеются функции с ограниченной областью определения, то область определения исходной функции не шире их области определения. (Например, обратные тригонометрические функции или функции tg(x), ctg(x) и т. д.)

Например, функция:

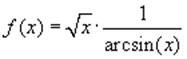
имеет область определения:
а) arcsin имеет область определения от -1 до 1;
б) x>=0 (т. к. x подкоренное выражение);
в) arcsin(x) не равен нулю, т. е. x не равно нулю (т. к. arcsin(x) выражение в знаменателе).

Таким образом, область определения функции x принадлежит (0,1].

Дифференциал функции и его геометрический смысл. Связь с производной.

Дифференциал функции — приращение функции:

- главная часть;

- не главная часть.

Если к графику гладкой функции в некоторой точке построить касательную, то, отложив на касательной такой отрезок, чтобы его проекция на ось Ох равнялась ∆Х, получим в проекции на ось Оу отрезок, равный дифференциалу функции в точке касания.

∆y = dy + 0(∆x)

dy/dx = tgℓ = y'

dy = y' * ∆x

∆x = dx

dy = y' * dy

y' = dy/dx

Таблица основных интегралов.

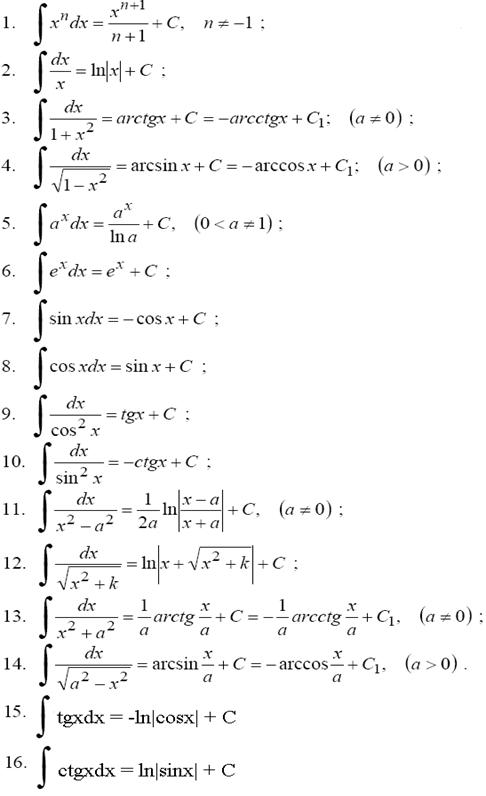
Методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.

Непосредственное интегрирование: Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

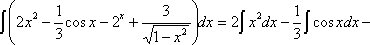
Замена переменной: Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.

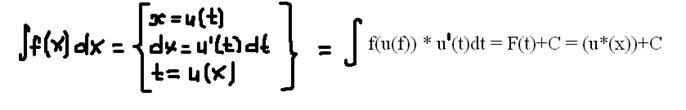
Интегрирование по частям — применение следующей формулы для интегрирования: