Тема 3: Интегральное исчисление функции одной переменной
23. Неопределенный интеграл (первообразная функции, определение неопределенного интеграла, геометрическое значение неопределенного интеграла, свойства).
Функция F(x) называется первообразной для функции f(х) на промежутке Х, если для всех значений х из того промежутка выполняется равенство
F'(x) = f(х) (или dF(x)=f(x)dx).
Множество всех первообразных функций F(x)+С на промежутке Х для функции f(х) называется неопределенным интегралом от функции f(х) и обозначается символом  .
.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у=F(x)+С (каждому числовому значению С соответствует определенная кривая семейства).
1°. Производная неопределенного интеграла равна подынтегральной функции, т.е.

∆ Дифференцируя левую и правую части равенства (1), получаем
 .
.
2°. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

По определению дифференциала и свойству 1 имеем
 .
.
3°. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
∫dF(x)=F(x)+C
где С – произвольное число.
4°. Постоянный множитель можно выносить за знак интеграла, т.е.
∫ κf(x)dx=κ ∫f(x)dx ,
5°. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
∫ (f(x) ± g(x)) dx = ∫f(x)dx ± ∫g(x)dx.
6°. Если F(x) – первообразная для f(x), то  - первообразная для функции f(κx+b), т.е.
- первообразная для функции f(κx+b), т.е.

(κ≠0)
24. Таблица основных интегралов.
Таблица основных интегралов
1. 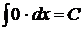 . 11.
. 11. 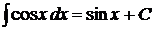 .
.
2. 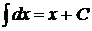 . 12.
. 12. 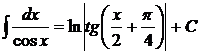 .
.
3. 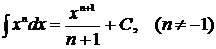 . 13.
. 13. 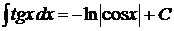 .
.
4. 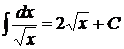 . 14.
. 14. 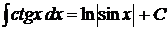 .
.
5. 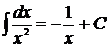 . 15.
. 15. 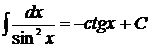 .
.
6. 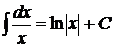 . 16.
. 16. 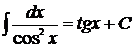 .
.
7. 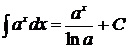 . 17.
. 17. 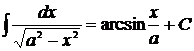 .
.
8. 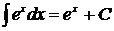 . 18.
. 18. 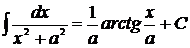 .
.
9. 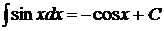 . 19.
. 19. 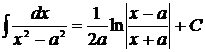 .
.
10. 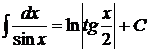 . 20.
. 20. 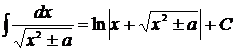 .
.
25. Непосредственное интегрирование (основное понятие, часто встречающиеся преобразования дифференциала).
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам называется непосредственным интегрированием.
Часто встречающиеся преобразования дифференциала:
1. Выражение не изменяется, если под знаком дифференциала к функции прибавить постоянную величину, т.е.
du=d(u+С), где С- число.
2. Если под знаком дифференциала функцию умножить на постоянную величину, все выражение нужно разделить на эту же постоянную величину, т.е.
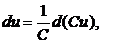 где С – число.
где С – число.
Формула 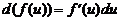 очень часто используется при вычислении интегралов. Например,
очень часто используется при вычислении интегралов. Например,
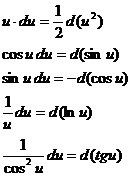
26. Метод подстановки в неопределенном интеграле (основное понятие, вывод формулы интегрирования).
Метод интегрирования подстановкой заключается во введение новой переменой интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 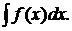 Сделаем подстановку
Сделаем подстановку 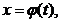 где
где 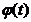 - функция, имеющая непрерывную производную.
- функция, имеющая непрерывную производную.
Тогда 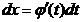 и получаем формулу интегрирования подстановкой
и получаем формулу интегрирования подстановкой
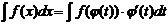 .
.
27. Интегрирование по частям в неопределенном интеграле (основное понятие, вывод формулы интегрирования).
Пусть u=u(x) и v=v(x) – функции, имеющие непрерывные производные. Тогда по правилу дифференцирования произведения имеем: 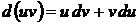 . Интегрируя это равенство, получим
. Интегрируя это равенство, получим 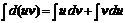 или
или
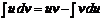
Полученная формула называется формулой интегрирования по частям. При ее применении подынтегральное выражение искомого интеграла разбивается на два сомножителя (u и dv). При переходе к правой части (2) первый из них дифференцируется ( 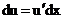 ), второй интегрируется
), второй интегрируется 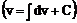 . Иногда эту формулу приходиться использовать несколько раз.
. Иногда эту формулу приходиться использовать несколько раз.
28. Правильные и неправильные рациональные дроби, выделение целой части у неправильной дроби (целая рациональная функция, дробно-рациональная функция, правильные и неправильные дроби, выделение целой части у неправильной дроби).
Целой рациональной функцией (многочленом) называется функция вида
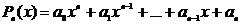 , (1)
, (1)
где а0, а1,…,аn – постоянные, называемые коэффициентами многочлена; число n – постоянная, называемая показателем степени многочлена.
Дробно-рациональной функцией (или рациональной дробью) называется функция, равная
отношению двух целых рациональных функций (многочленов), т.е. 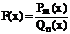 , где Рm(х)- многочлен степени m, а Qn(x)- многочлен степени n.
, где Рm(х)- многочлен степени m, а Qn(x)- многочлен степени n.
Дробно-рациональная функция называется правильной, если степень числителя меньше степени знаменателя, т.е. m<n; в противном случае ( 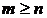 ) функция называется неправильной.
) функция называется неправильной.
Всякую неправильную дробно-рациональную функцию 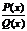 можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(х) и правильной рациональной функции
можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(х) и правильной рациональной функции 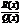 , т.е.
, т.е. 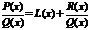 .
.
29. Разложение правильной дроби на сумму простейших дробей, метод сравнивания коэффициентов (четыре основных вида простых дробей, три случая разложения правильных дробей на простейшие дроби, алгоритм метода сравнивания коэффициентов).
Простыми дробями называют дроби следующих типов:
1) 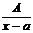 ; 2)
; 2) 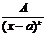 ; 3)
; 3) 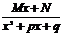 ; 4)
; 4) 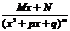 ,
,
где A, M, N, a, p, q – действительные числа, k=2,3,…., m=2,3,….., квадратный трехчлен x2+px+q не имеет корней.
Рассмотрим 3 случая разложения дробно-рациональных функций:
1) Множители знаменателя линейные, они различны. Количество простых дробей равно показателю степени знаменателя.
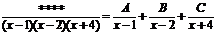 .
.
2) Наряду с линейными различными множителями знаменателя (которых может и не быть) присутствуют повторяющиеся линейные множители. Количество простых дробей равно показателю степени знаменателя.
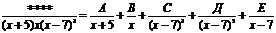 .
.
3) Наряду с линейными множителями знаменателя встречаются выражения второй степени, не разлагающиеся на линейные множители.
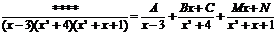 .
.
