Случайные события. Операции со случайными событиями

Опр. Событие, которое при одних и тех же условиях может наступить, либо не наступить называется случайным событием A,B,C.

Операции со случайными событиями:

Число А называется подсобытие события В, если из наступления события А следует наступление события В.

Противоположным событием вектора А к событию А называется событие заключающейся в том, что событие А не наступает.

Опр. Если А является пособытием события В, то А благоприятно для В.

Опр.Сумма двух случайных событий А+В называется событие С, которое состоит в том, что наступает или событие А, или В, или оба вместе.

А+В=С

Опр.Произведением А*В называется заключающееся в том, что наступает и событие А и событие В одновременно.

Опр.Если А*В= 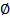есть событие невозможное, то такие события называются не совместными.

Классическое определение вероятности

Классическое определение вероятности

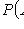
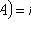
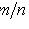
(m - число благоприятных исходов опыта; n - число всех его исходов)

Под вероятностью случайного события понимают, некоторую объективную характеристику того, на сколько часто это событие может наступать.

Свойства вероятностей событий

·

·

·

·

·

·

·

·

·

·

·

·

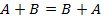
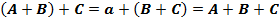
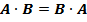
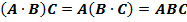
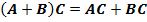
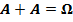
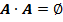
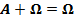
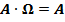
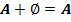
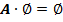
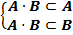
Опр.Н₁, Н₂…Н_n – образуют полную группу событий, если они удовлетворяют двум свойствам:

1.

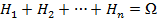
2.

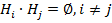
Теорема сложения вероятностей.

Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

Следствие 1: Если события образуют полную группу несовместных событий, то сумма их вероятностей равна единице.

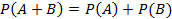
Условная вероятность. Теорема умножения вероятностей определение независимых случайных событий.

Произведения событий А и В называется событием состоящем в появлении этих событий.

События А и В называются независимыми, когда события независят от другого.

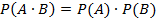
Формула полной вероятности

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) B₁, В₂,...,В_n, образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

Р(А) = Р (В₁) Р_В1(А) + Р (В₂) Р_В2(А) + ... + Р (В_n) Р_Вn(А). (*)

где Р(В₁)+Р(В₂)+...+Р(В_n)=1.

Формула Байеса

,

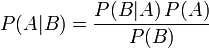где

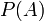— априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

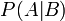— вероятность гипотезы A при наступлении события B (апостериорная вероятность);

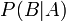— вероятность наступления события B при истинности гипотезы A;

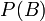— полная вероятность наступления события B.

Формула Бернулли

Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность 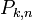того, что событие A наступит k раз в n независимых испытаниях, равна: 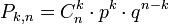, где .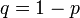

Дискретные случайные величины. Таблица распределения

ОПРЕДЕЛЕНИЕ. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая – их вероятности:

X	x1	x2	...	xn
P	p1	p2	...	pn