Смешанное произведение в координатах

Если векторы заданы собственными координатами, то произведение вычисляется матричным способом

Условия коллинеарности, ортогональности, компланарности векторов

Условие коллинеарности векторов a(x,y), b(x2,y2)

=

Условие ортогональности: Скалярное произведение должно = 0

(ab)=0

Условия компланарности:

Три вектора компланарны, если их смешанное произведение равно нулю.

Три вектора компланарны, если они линейно зависимы.

Нормальное уравнение плоскости

n⁰r-p=0

Нормально уравнение плоскости в векторной плоскости

xcosα+ycosβ+zcos -p=0

Общее уравнение плоскости. Частные случаи расположения плоскости

Ax+By+Cz+D=0

Частные случаи расположения плоскости

1) D=0 Плоскость проходит через начало координат

2) C=0 или B=0 или A=0, плоскость параллельна оси отсутствующего элемента

3) D=0 и C=0 или B=0 или A=0, плоскость проходит через ось отсутствующего элемента

4) B,C=0 или A,C=0 или A,B=0, плоскость параллельна плоскости отсутствующих элементов

5) D=0 и B,C=0 или A,C=0 или A,B=0, плоскость лежит в плоскости оставшегося элемента

Уравнение плоскости в отрезках

+ + =1

Уравнение плоскости, проходящей через данную точку

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

Уравнение плоскости, проходящей через 3 точки

(Матрица)

Угол между плоскостями. Условия параллельности и перпендикулярности прямых

Ax+By+Cz+D=0 n(A,B,C)

cosφ=

Если плоскости параллельны, то n2 следовательно = =

Если плоскости перпендикулярны, то n1 n2, n1n2=0 A1A2+B1B2+C1C2=0

Расстояние от точки до плоскости

D=

Общее уравнение прямой в R³

Прямая как пересечение двух плоскостей

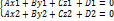
Векторное уравнение прямой

R=ts+r₀

Параметрическое и каноническое уравнение прямой

Параметрическое

r₀(x₀,y₀,z₀)

s(m,n,p)

r(x,y,z)

Каноническое (исключаем параметр t)

= =

Cosα=m/׀s׀

Уравнение прямой проходящей через две заданные точки

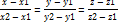
Приведение общего уравнения прямой к каноническому виду

S=n1*n2

S=

Угол между прямыми. Условие параллельности и перпендикулярности

Cosφ=

s1 , то

s1⊥s2, то m1m2+n1n2+p1p2=0

Прямая линия на плоскости. Нормальное уравнение прямой

Ах+Ву+D=0

xcosα+ycosβ-p=0

Общее уравнение прямой. Исследование общего уравнения прямой

Ах+Ву+D=0

1) D=0, прямая проходит через начало координат (0,0,0)

2) A=0 или B=0, прямая параллельна оси отсутствующего элемента

3) D=0 и A=0 или B=0, уравнение оси отсутствующего элемента

Уравнение прямой проходящей через данную точку в данном направлении

y - y₁ = k(x - x₁)

Уравнение прямой проходящей через две заданные точки

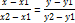
Угол между прямыми

cosφ=

Условие параллельности и перпендикулярности прямых

Если плоскости параллельны, то n2 следовательно =

Если плоскости перпендикулярны, то n1 n2, n1n2=0 A1A2+B1B2 =0

Уравнение прямой в отрезках

+ + =1

Расстояние от точки до прямой. Уравнение прямой с угловым коэффициентом.

D=

y=kx+b

Угол между двумя прямыми. Условие параллельности и перпендикулярности

y=k1x+b1 k1=tgα1

y=k2x+b2 k2=tgα2

φ=α1-α2

k1=-1/k2

если ⊥ , то φ=0 tgφ=0

если паралл, то k1=k2