Определитель (детерминант) матрицы. Свойства определителя

Матрицы. Основные понятия. Линейные операции над матрицами и их свойства

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа из которых составляется матрица называются элементами матрицы. Матрица состоящая из одной строки – строчная, из одного столбца – столбцовая матрица, если столб=строк= квадратная матрица, все элементы 0 – нулевая матрица. Диагональная матрица – квадратная матрица у которой отличной от 0 только элементы главной диагонали. Единичная матрица – матрица у кот.каждый элемента главной диагонали = 1. Симметричная М это квадратная М для которой а_ij=a_ij, симметрично вокруг главной диагонали. Трапециидная М. Треугольная М – частный случайтрапециидной М (квадратная матрица у которой по одну сторону от главной диагонали элементы равны 0). Единичная Е – все элементы = 1

Для того чтобы умножить М А на число с, нужно все элементы М умножить на число с. Св-ва с=1 сА=А, с=0 сА=0, с(кА)=(ск)А

Складывать можно М одинаковых размеров. Св-ва А+В=В+А; с(А+В)=сА+сВ ...

Определитель (детерминант) матрицы. Свойства определителя

Численная характеристика квадратной матрицы называется ее определителем. Св-ва:

1. При замене строк столбцами величина определителя не меняется.

2. Если поменять 2 строки или 2 столбца определитель поменяет знак.

3. Определитель с двумя одинаковыми рядами равен 0

4. Величина определителя увеличивается в К раз если элементы какого либо его ряда увеличены в К раз

5. Величина определителя =0, если элементы какого либо его ряда =0

6. Определитель, у которого элементы двух строк или столбцов пропорциональны = 0

7. Определитель, у которого элементы какого либо ряда представлены суммой двух слагаемых, = сумме двух определителей.

8. Определитель = сумме произведений элементов какого либо ряда на их алгебраическое дополнение.

9. Величина определителя не изменится, если к элементам какого либо ряда + соотв элементы другого ряда умноженных на число К

Миноры и алгебраические дополнения

Минором М_ija_ij называется определитель, который получается путем вычеркивания строки с номером i и столбца с номером j

Алгебраическим дополнение A_ij для элемента a_ij называетсяего Минор взятый со знаком (-1)^i+j(на нечетных местах меняется знак на -)

Теорема замещения

Сумма произведений произвольных n чисел (с1,с2,с3,сn) на алгебраические дополнения какого либо ряда М порядка n, = определителю матрицы, которая получается из данных, заменой элементов указанного ряда на числа c1,c2,c3

Теорема аннулирования

Сумма произведения элементов одного из рядов определителя на алгебраическое дополнения элементов другого, параллельного ему ряда = 0

Некоторые методы вычисления определителей

Приведение определителя к треугольному виду. Состоит в таком его преобразовании, когда все элементы, лежащие по одну сторону главной диагонали, становятся нулями. Полученный определитель равен произведению элементов главной диагонали

По правилу треугольника

По правилу Саррюса

Умножения матриц. Свойства умножения

. Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матриц согласована. Св-ва АВ ВА, с(АВ)=(сА)В=А(сВ), …

Транспонирование матриц

М полученная из данных путем замены каждой ее строки столбцом того же номера, называю транспонированной. Определитель транспонированной матрицы равен определителю исходной матрицы

Матричная запись системы линейных уравнений и ее решение

В матричном виде линейные уравнения записываются как AX=B, где А, коэффициенты при х, х =есть неизвестные, в = их значения. Решаются с помощью обратной матрицы

Уравнение плоскости, проходящей через данную точку

A(x-x₀)+B(y-y₀)+C(z-z₀)=0

Уравнение плоскости, проходящей через 3 точки

(Матрица)

Векторное уравнение прямой

R=ts+r₀

Параметрическое и каноническое уравнение прямой

Параметрическое

r₀(x₀,y₀,z₀)

s(m,n,p)

r(x,y,z)

Каноническое (исключаем параметр t)

= =

Cosα=m/׀s׀

Угол между прямыми

cosφ=

Уравнение прямой в отрезках

+ + =1

Расстояние от точки до прямой. Уравнение прямой с угловым коэффициентом.

D=

y=kx+b

Цилиндрические поверхности

Поверхность образованная движением образующей (L), которая перемещается в пространстве, сохраняя при это направление и каждый раз пересекая направляющую (K) называется цилиндрической поверхностью или цилиндр

Название цилиндра определяется названием образующей: Эллиптическая (по эллипсу, уравнение эллипса), Круговая…

Эллипсоиды

=1

Гиперболоид

= 1

Параболоид

x²+y²=2px

Конические поверхности

Поверхность, образуемая движением линии АВ , перемещающуюся в пространстве так, что она постоянно проходит через вершину и пересекает направляющую

Функция. Основные понятия. Способы ее задания

Функция- соответствие f, которое каждому элементу x сопоставляет только один у

Множество Х называется областью определения

Множество У называется областью значения

Если элементами х и у являются действительные числа то функция называется числовой

Три способа задания функции: графический, аналитический, табличный

Конечный предел функции

Предел равен конкретному числу

Бесконечный предел функции

Предел равен бесконечности

Односторонние пределы

Число В называется пределом функции слева при х→а, если для любой а последовательности аргументов функции х, значение которых остаются меньше а, последовательность значений этой функции сходится к В

Число В называется пределом функции справа при х→а, если для любой а последовательности аргументов функции х, значение которых остаются меньше а, последовательность значений этой функции сходится к В

Теорема сравнения

Если в окрестности одна функция меньше другой и они имеют предел, то f(x)<g(x) → <

Если функция в окрестности ограничена слева и справа функциями имеющими равные пределы, то существует предел у внутренней функции и он равен двум другим

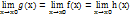
Первый замечательный предел

Предел отношения синуса к его аргументу равен единице, когда аргумент стремиться к нулю

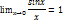
Второй замечательный предел

Второй замечательный предел имеет вид:

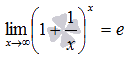
или в другой записи

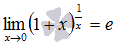
Производная сложной функции

7) сложная функция равна y=f(u), где u=φ(x) → y_x`=y<sub>u</sub>` u_x`

Теорема Коши

Если функции f(x) и φ(x) непрерывны на отрезке [a,b] и дифференцируемsна интервале (a,b) ,причем φ`(x)≠0 для x∈(a;b) , то найдется хотя бы одна точка c∈(a;b) такая, что выполняется неравенство:

Матрицы. Основные понятия. Линейные операции над матрицами и их свойства

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа из которых составляется матрица называются элементами матрицы. Матрица состоящая из одной строки – строчная, из одного столбца – столбцовая матрица, если столб=строк= квадратная матрица, все элементы 0 – нулевая матрица. Диагональная матрица – квадратная матрица у которой отличной от 0 только элементы главной диагонали. Единичная матрица – матрица у кот.каждый элемента главной диагонали = 1. Симметричная М это квадратная М для которой а_ij=a_ij, симметрично вокруг главной диагонали. Трапециидная М. Треугольная М – частный случайтрапециидной М (квадратная матрица у которой по одну сторону от главной диагонали элементы равны 0). Единичная Е – все элементы = 1

Для того чтобы умножить М А на число с, нужно все элементы М умножить на число с. Св-ва с=1 сА=А, с=0 сА=0, с(кА)=(ск)А

Складывать можно М одинаковых размеров. Св-ва А+В=В+А; с(А+В)=сА+сВ ...

Определитель (детерминант) матрицы. Свойства определителя

Численная характеристика квадратной матрицы называется ее определителем. Св-ва:

1. При замене строк столбцами величина определителя не меняется.

2. Если поменять 2 строки или 2 столбца определитель поменяет знак.

3. Определитель с двумя одинаковыми рядами равен 0

4. Величина определителя увеличивается в К раз если элементы какого либо его ряда увеличены в К раз

5. Величина определителя =0, если элементы какого либо его ряда =0

6. Определитель, у которого элементы двух строк или столбцов пропорциональны = 0

7. Определитель, у которого элементы какого либо ряда представлены суммой двух слагаемых, = сумме двух определителей.

8. Определитель = сумме произведений элементов какого либо ряда на их алгебраическое дополнение.

9. Величина определителя не изменится, если к элементам какого либо ряда + соотв элементы другого ряда умноженных на число К