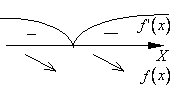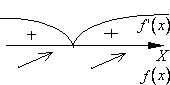Признаки постоянства, возрастания и убывания функций на промежутке
Необходимое и достаточное условие постоянства функции y = f ( x ) выражается равенством y ’ = 0.
Если производная функции на участке существует и равна нулю и функция определена на данном участке, то функция на данном участке постоянна.
Определение возрастающей функции.
Функция y=f(x) называется возрастающей в промежутке (a,b), если для любых двух значений x1 и x2 из неравенства x1<x2 следует неравенство f(x1)<f(x2).
Функция y=f(x) возрастает на интервале X, если для любых 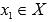 и
и 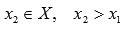 выполняется неравенство
выполняется неравенство 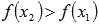 . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Определение убывающей функции.
Функция y=f(x) называется убывающей в промежутке (a,b), если для любых двух значений x1 и x2 из неравенства x1<x2 следует неравенство f(x1)>f(x2).
Функция y=f(x) убывает на интервале X, если для любых 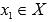 и
и 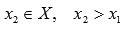 выполняется неравенство
выполняется неравенство 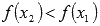 . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.
Нахождение максимумов и минимумов функции с помощью производных
Определение: Говорят, что функция 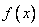 имеет в точке
имеет в точке 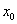 максимум , ( или минимум) , если существует некоторая окрестность
максимум , ( или минимум) , если существует некоторая окрестность 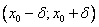 в промежутке, где функция определена, что для всех точек этой окрестности выполняется неравенство
в промежутке, где функция определена, что для всех точек этой окрестности выполняется неравенство 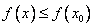 (
( 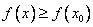 ).
).
Пусть функция 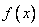 определена на некотором промежутке и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная
определена на некотором промежутке и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная 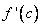 , то необходимо
, то необходимо 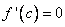 .
.
Определение: Если выполняется равенство 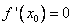 , то точку
, то точку 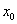 будем называть стационарной точкой.
будем называть стационарной точкой.
Определение: Стационарные точки и точки, в которых не существует двусторонней конечной производной, будем называть точками, подозрительными на экстремум.
Предположим, что в некоторой окрестности 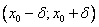 стационарной точки
стационарной точки 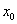 существует конечная производная
существует конечная производная 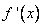 и как слева от
и как слева от 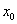 ,так и справа от
,так и справа от 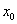 ( в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:
( в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:
1) 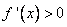 при
при 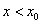 и
и 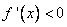 при
при 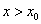 (производная
(производная 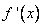 при переходе через точку
при переходе через точку 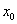 меняет свой знак с плюса на минус). Т.е. при
меняет свой знак с плюса на минус). Т.е. при 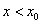 функция возрастает, а при
функция возрастает, а при 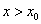 — убывает. Значит, значение
— убывает. Значит, значение 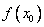 будет наибольшим в промежутке
будет наибольшим в промежутке 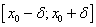 . Другими словами, в точке
. Другими словами, в точке 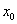 функция имеет максимум.
функция имеет максимум.
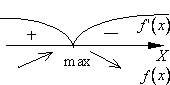
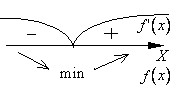
Пояснение: Сверху от числовой оси указывается знак производной на соответствующем интервале, снизу от числовой оси обозначается поведение функции на соответствующем интервале (убывание или возрастание).
2) 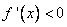 при
при 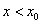 и
и 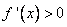 при
при 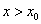 (производная
(производная 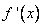 при переходе через точку
при переходе через точку 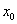 меняет свой знак с минуса на плюс). Т.е. при
меняет свой знак с минуса на плюс). Т.е. при 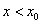 функция
функция 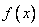 убывает, а при
убывает, а при 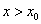 — возрастает. Значит, значение
— возрастает. Значит, значение 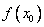 будет наименьшим в промежутке
будет наименьшим в промежутке 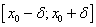 . Другими словами, в точке
. Другими словами, в точке 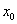 функция имеет минимум.
функция имеет минимум.
3) 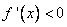 при
при 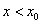 и
и 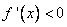 при
при 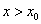 (
( 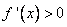 при
при 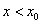 и
и 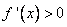 при
при 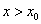 )(производная
)(производная 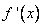 при переходе через точку
при переходе через точку 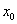 не меняет свой знак). Т.е. функция
не меняет свой знак). Т.е. функция 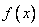 в промежутке
в промежутке 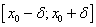 убывает (возрастает). Другими словами, в точке
убывает (возрастает). Другими словами, в точке 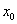 функция
функция 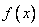 не имеет экстремума.
не имеет экстремума.