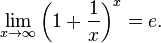Свойства пределов функции, связанные с арифметическими действиями и неравенствами.

· Предел суммы/разности двух функций равен сумме/разности их пределов:

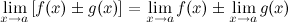
· Предел произведения двух функций равен произведению их пределов:

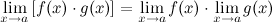
· Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

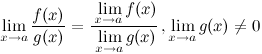
· Константу можно выносить за знак предела:

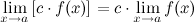
· Предел степени с натуральным показателем равен степени предела:

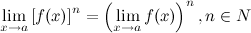
Предел сложной функции

Если функция y=f(x) имеет в точке a конечный предел b и не принимает значение b в некоторой проколотой окрестности U(a) этой точки, а функция g(y) имеет в точке конечный предел c, то сложная функция g(f(x)) имеет предел в точке a и он равен c.

Односторонние пределы

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (пределом справа).

Предел монотонной функции.

Монотонная функция — это функция, приращение которой не меняет знака, то есть либо всегда не отрицательное, либо всегда не положительное. Если в дополнение приращение не равно нулю, то функция называется строго монотонной. Монотонная функция — это функция, меняющаяся в одном и том же направлении.

Если функция f(x) определена и монотонна на отрезке [a;b], то в каждой точке x (a;b) эта функция имеет конечные пределы слева и справа, а в точках a и b правосторонний и левосторонний пределы.

Бесконечно большие, бесконечно малые и эквивалентные величины, о- символика.

Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.

Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Если 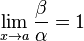, то бесконечно малые или бесконечно большие величины 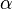и 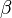называются эквивалентными (обозначается как ).

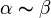«O» большое и «o» малое (O и o) — математические обозначения для сравнения асимптотического поведения функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также в информатике и теории алгоритмов.

o(f), «о малое от f» обозначает «бесконечно малое относительно f», пренебрежимо малую величину при рассмотрении f. Смысл термина «О большое» зависит от его области применения, но всегда O(f) растёт не быстрее, чем f.

Основные виды неопределенностей

Раскрытиенеопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

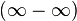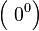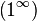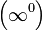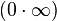(Здесь 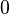— бесконечно малая величина, а 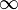— бесконечно большая величина)

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Замечательные пределы

Замечательные пределы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:

Первый замечательный предел:

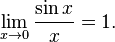
Второй замечательный предел: