Практические занятия по разделу 6.

«Кратные, криволинейные интегралы».

Вопросы для самостоятельной работы

1. Что называется двойным интегралом от функции f(x,у) по плоской области Д? Назовите геометрический смысл двойного интеграла.

2. Укажите правила расстановки пределов интегрирования при переходе от двойного интеграла к двукратному.

3. Укажите способ вычисления двойного интеграла, если область интегрирования есть прямоугольник со сторонами, параллельными осям координат.

4. Вычисление двойного интеграла в полярных координатах.

5. Повторите построение плоскостей, цилиндров и параболоидов. В чем состоит «метод параллельных сечений»? Сформулируйте понятие образующей и направляющей цилиндрической поверхности.

6. Вычисление объема тела с помощью двойного и тройного интеграла.

7. Вычисление криволинейного интеграла II рода

8. Зависимость значения криволинейного интеграла от направления обхода контура интегрирования.

9. Укажите условия независимости криволинейного интеграла от пути интегрирования.

10. Укажите правило нахождения функции двух переменных по ее полному дифференциалу.

Задача 1. Вычислить 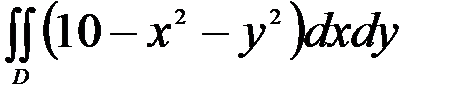, если область Д ограничена прямыми x=1, x=2, y=0, y=2.

Решение 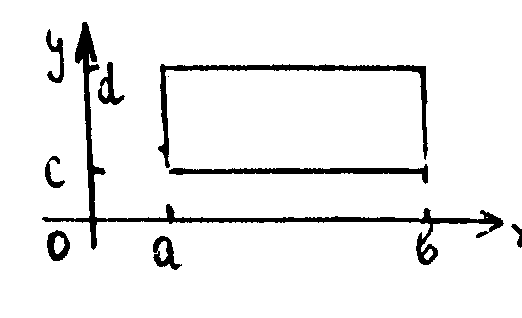. Известно, что, если область интегрирования Д есть прямоугольник со сторонами x=a, x=b, y=c, y=d, то вычислением двойного интеграла производится по формуле

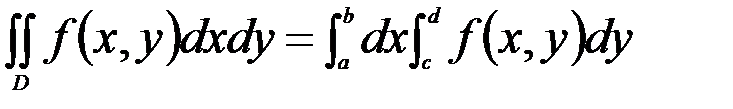(1)

или

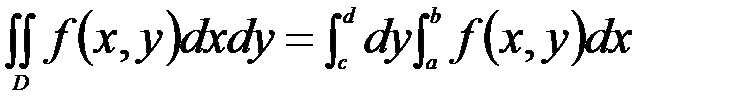(2)

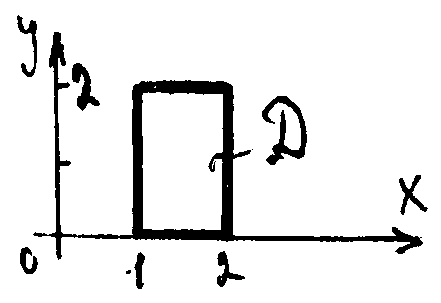Изобразим данную область Д. По формуле (1) имеем

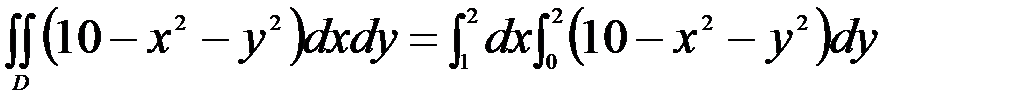
Внутренний интеграл вычисляем, считая x постоянной величиной:

.

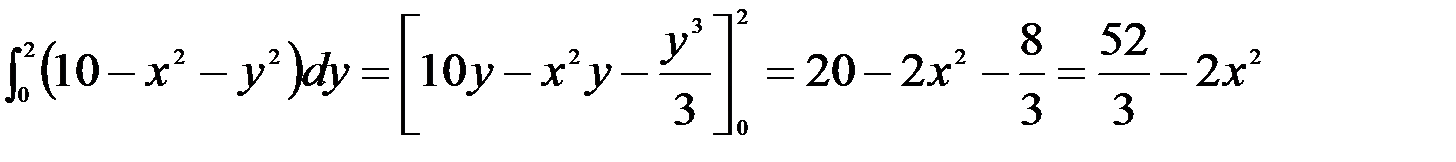Полученную функцию 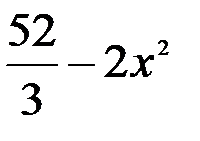интегрируем на отрезке [1;2] оси OX:

.

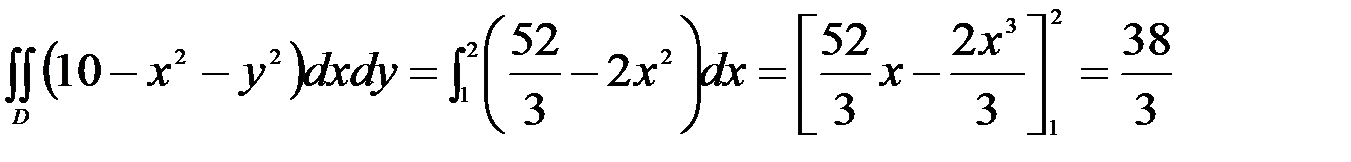Задача 2 Дан интеграл .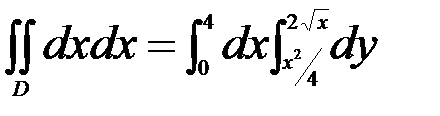

Требуется: 1) построить на плоскости XOУ область интегрирования; 2) изменить порядок интегрирования; 3) вычислить площадь области Д при заданном и измененном порядках интегрирования.

Решение. 1) Построим область интегрирования Д, используя известные пределы данного двукратного интеграла. Так как внутренний интеграл взят по y, то его пределы получены из уравнений 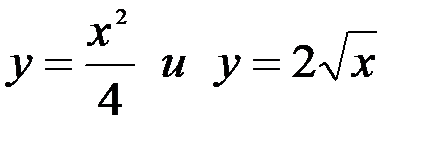, которые определяют соответственно нижнюю и верхнюю границы области Д. Слева и справа она ограничена прямыми x=0, и x=4. Найдем координаты точки A пересечения кривых:

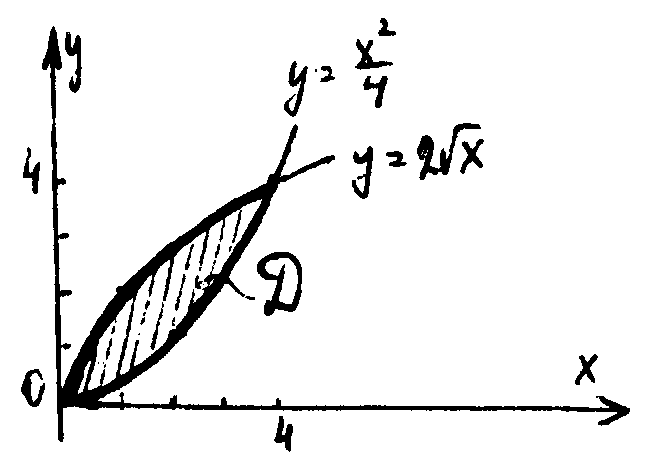
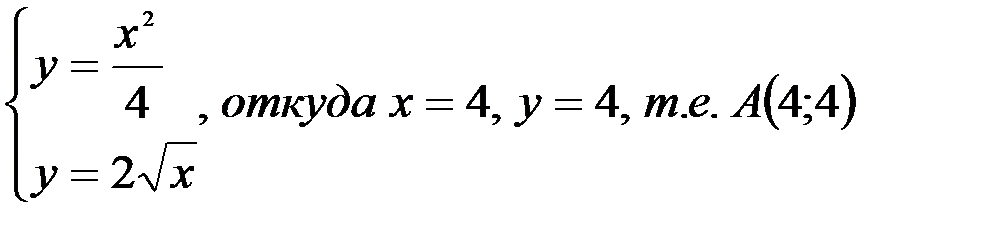
Известно, что двойной интеграл вычисляется по формуле

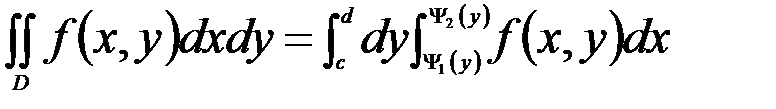(2),

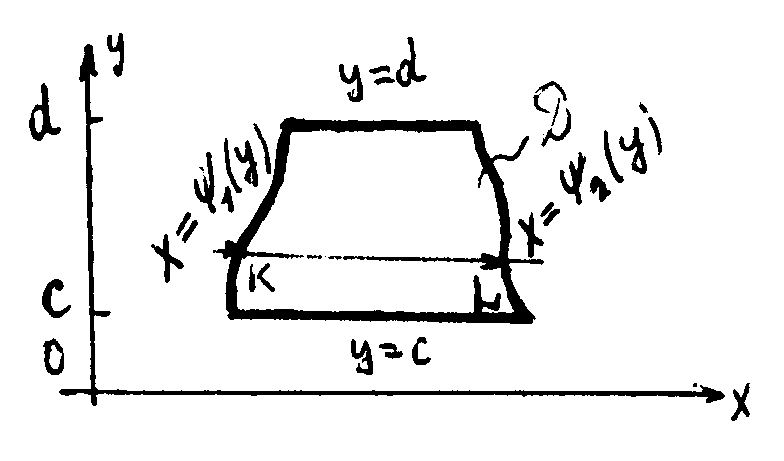
если область Д ограничена слева линией X=ψ₁(y), справа - линией X=ψ₂(y), сверху и снизу прямыми Y=d и Y=с, причем всякая прямая, параллельная оси OX, пересекает границу области Д не более чем в двух точках (K и L). Поэтому при изменении порядка интегрирования данный двойной интеграл примет следующий вид двукратного интеграла:

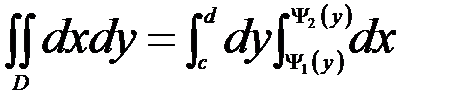
Определим в нем пределы по Y и по X, используя рисунок. Сначала выразим переменную X из уравнения 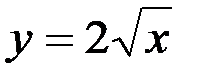: получим уравнение 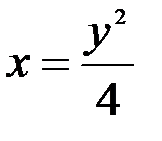(левая граница области Д). Далее из уравнения 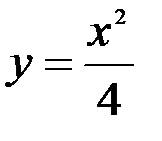получим уравнение 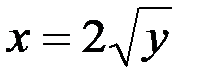(правая граница области Д). Следовательно, область Д определяется неравенствами:

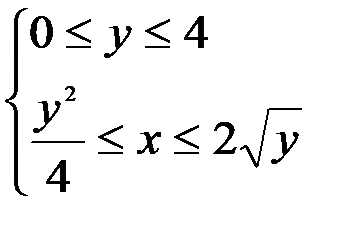
Тогда .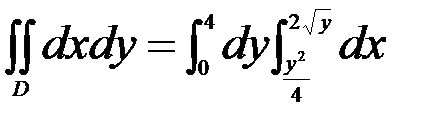

3) Площадь плоской области Д определяется по формуле

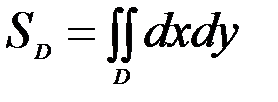(3)

Тогда при заданном порядке интегрирования получим:

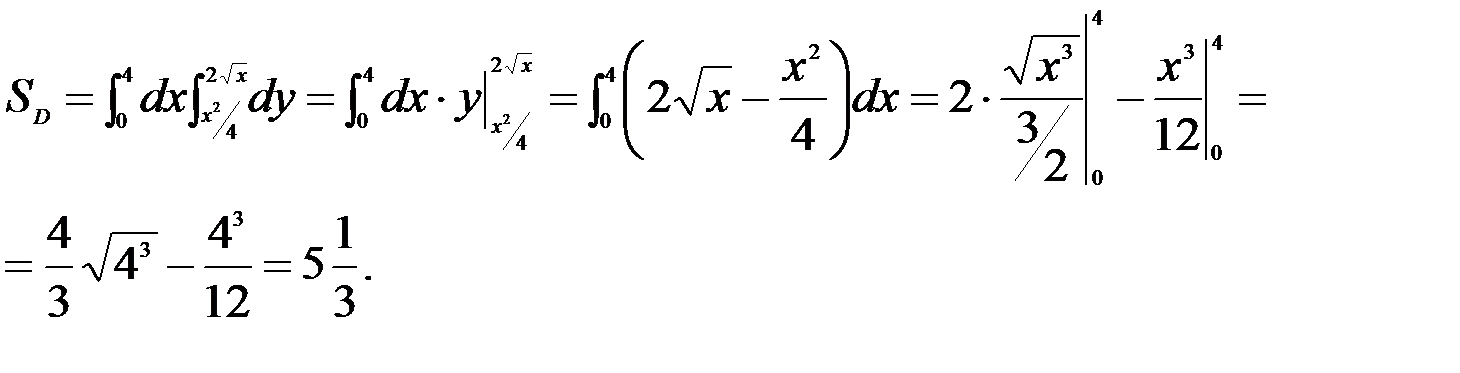
Определим площадь области Д при измененном порядке интегрирования:

.

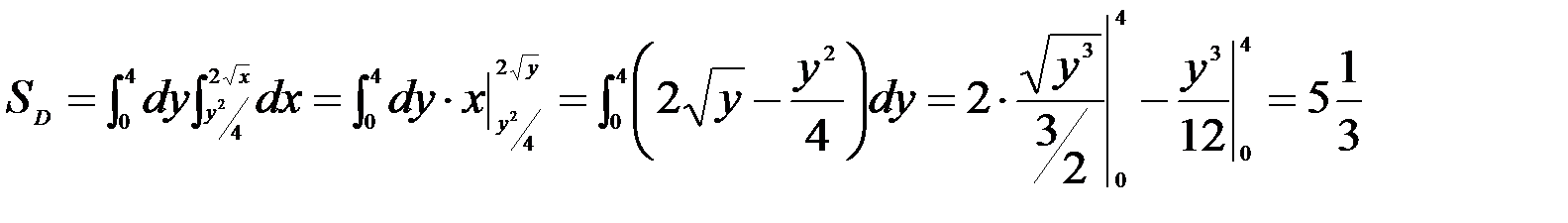Задача 3. Построить плоскость 2x+3y+6z=0.

Решение 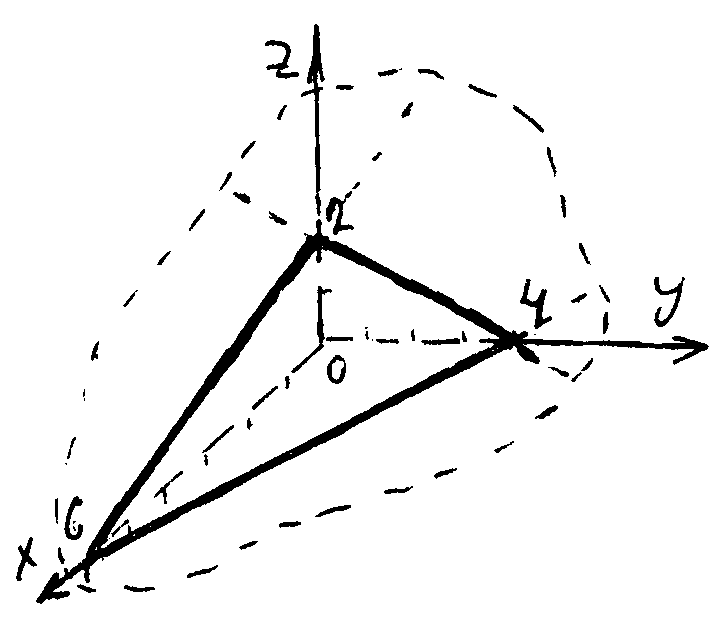. Для построения плоскости по уравнению достаточно построить три ее точки, не лежащие на одной прямой. Две координаты точек берут произвольно, а третью из уравнения. Легче всего определить точки пересечения плоскости с осями координат. Составим таблицу значений x, y, z для трех точек:

xx	y y	z z

Строим точки A(0;0;2), B(6;0;0), C(0;4;0) и соединяем их прямыми линиями.

№ пп/п	Каноническое уравнение	Схематичес-кое изображение	Название поверх-ности
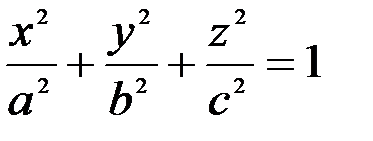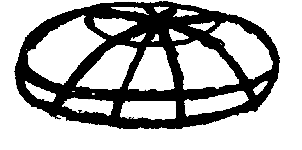			Эллипсоид (в частности, эллипсоид вращения и сфера)
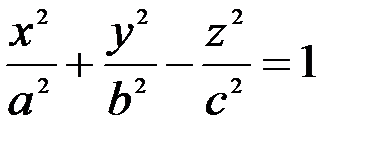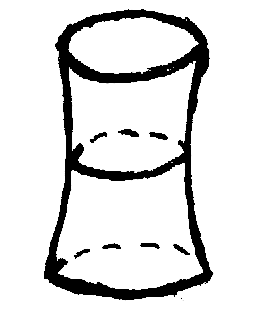			Однополосный гиперболоид
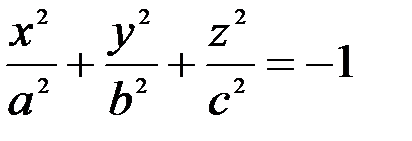			Двуполосный гиперболоид
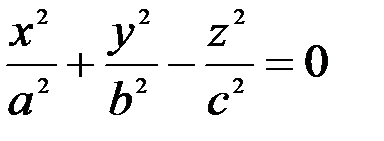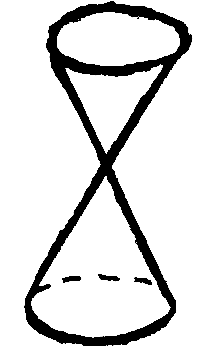			Конус второго порядка