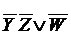Недоопределенных БФ методом проб.

Будем полагать, что БФ задана таблично кодами конъюнкций D₁и D₀.

Любая конъюнкция К из D₁ такова, что:

1) M₁(К)ÇM₁(F)¹ Æ -конъюнкция К из множества М1 входит в множество М₁(F).

2) M₁(К)ÇM₀(F) = Æ -конъюнкция К из множества М1 не входит в множество М₀(F). Нет такого набора значений переменных, на котором БФ одновременно определяется равной и 1 и 0.

Если максимально укоротить конъюнкцию К так, чтобы условия 1) и 2) попрежнему выполнялись, то мы получим простую импликанту.

Выполнимость условия 1) вытекает из того, что если К* получена из К вычеркиванием букв, то M₁(К*) É M₁(К).

Доказательство.

Если переменная 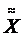в конъюнкции К вызывает вхождение в M₁(К) наборов со значением Х равным b, то вычеркивая Х, мы увеличим M₁(К) за счет наборов с противоположным значением (1-b).

Рассмотрим пример.

Пусть F=(X,Y,Z,W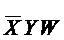). K= K*=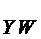

Тогда M₁(К)=(0101,0111).

M₁(K*) содержит наборы M₁(К) и кроме того наборы (1101,1111).

Процедура построения ДНФ эквивалентной D₁, но состоящей из простых импликант может быть такой:

1. Берем любую К конъюнкцию из D₁.

2. Максимально укорачивая К, строим простую импликанту и выписываем ее.

3. Удаляем из D₁ конъюнкции поглощаемые К.

4. Если D₁пусто кончаем, иначе идем к пункту 1.

Примечание.

Конъюнкция А поглощает конъюнкцию В, если константные значения кода А, тоесть все значения кроме «-», входят составной частью в код В.

Рассмотрим пример.

А = ( - 0 0 - ) ;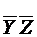

В = ( - 0 0 1 );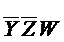

Удаляя из К одну за другой буквы, мы должны проверять не нарушается ли условие 2).

Если нарушается, то букву восстанавливаем, если нет, то оставляем удаленной.

Проверив все буквы в К, мы добьемся ее максимального укорачивания, то-есть получения из нее простой импликанты.

Проверка 2) выполняется так.

После вычеркивания буквы, берется код К и поочередно сравнивается со всеми кодами конъюнкций D₀. Если для любой пары сравниваемых кодов хотя бы в одном разряде значения противоположны ( 0 и 1), то нет набора, на котором К и D₀ одновременно равны «1», а значит можно вычеркивать данную переменную.

В противном случае, вычеркнутая (пробно!) буква должна быть восстановлена, так как ее удаление приводит к нарушению условия 2).

Процедуру построения ДНФ из простых импликант проиллюстрируем примером.

X	Y	Z	W	F
			-
		-
	-
-
-	-
		-

D₁ =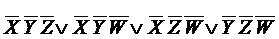

D₀ =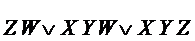

Берем из D₁ первую конъюнкцию: 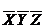(можно было бы взять и другую) и начинаем пробные вычеркивания букв.

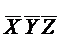(000-)

?

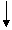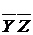(-00-)

Если конъюнкция 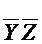(код -00-) такова, что М₁( 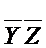)ÇМ₀ (F_~)¹Æ, то тогда есть набор, который можно получить по коду (-00-) и одновременно по коду хотя бы одной конъюнкции из D₀.

Так как код (-00-) ортогонален каждому коду из D₀, то набора принадлежащего и М₁( 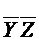) и М₀(F_~) не существует.

Ортогональность - наличие противоположных значений 0/1 хотя бы в одном разряде кодов.

Действительно:

(	-			-	)
(	-	-			)
(	-			-	)
(			-		)
(	-			-	)
(				-	)

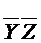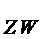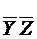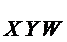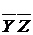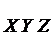Отсюда имеем первое укорачивание и переход к следующему пробному вычеркиванию.

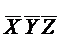(000-)

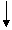
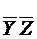(-00-)

?

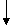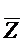(--0-)

Вычеркивание недопустимо, так как (--0-) не ортогонально с (11-1). Отсюда следует, что набор 1101 принадлежит и М₁ и М₀, а этого быть не может. Следовательно, вычеркивание невозможно и нужно новое пробное вычеркивание. Восстанавливаем вычеркнутую букву.

Пробуем вычеркнуть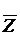

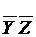(-00-)

?

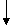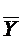(-0--)

Вычеркивание недопустимо, так как (-0--) не ортогонально с (--11). Отсюда следует, что набор 0011 принадлежит и М₁ и М₀, а этого быть не может. Следовательно, вычеркивание невозможно.

В итоге мы получили .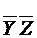

Константные значения кода (-00-), то есть все значения кроме « - », входят составной частью в коды (000-) и (-000). Следовательно, эта конъюнкция поглощает конъюнкции .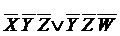

После выполнения поглощения, мы получим следующую таблицу:

X	Y	Z	W	F
		-
	-
-	-
		-
			-

Берем код 00-0 и выполняем пробное вычеркивание -0-0. Теперь выполним проверку на ортогональность с наборами из М₀.

-

-

-

-

-

-

-

-

-

-

Так как код (-0-0) ортогонален каждому коду из D₀, то набора принадлежащего и М₁( 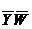) и М₀(F_~) не существует. Вычеркивание возможно.

Далее, попытаемся вычеркнуть следующую букву в коде -0-0. Выполним проверку на ортогональность с наборами из М₀ кода ---0.

-

-

-

-

-

-

-

-

-

-

-

-

-

Вычеркивание недопустимо, так как (---0) не ортогонально с (111-). Отсюда следует, что набор 1110 принадлежит и М₁ и М₀, а этого быть не может. Следовательно, вычеркивание невозможно и буква восстанавливается.

Теперь, попытаемся вычеркнуть другую букву в коде -0-0. Выполним проверку на ортогональность с наборами из М₀ кода -0---.

-

-

-

-

-

Вычеркивание недопустимо, так как (-0--) не ортогонально с (0011). Отсюда следует, что набор 0011 принадлежит и М₁ и М₀, а этого быть не может. Следовательно, вычеркивание невозможно.

Таким образом, получаем уще одну простую импликанту 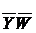, которая поглощает конъюнкцию .

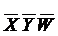В результате, у нас остается ода конъюнкция из М₁.

X	Y	Z	W	F
	-
-	-
		-
			-

Берем оставшийся код 0-00 и выполняем пробное вычеркивание --00. Теперь выполним проверку на ортогональность с наборами из М₀.

-

-

-

-

-

-

-

-

-

-

Так как код (-0-0) ортогонален каждому коду из D₀, то набора принадлежащего и М₁( 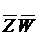) и М₀(F_~) не существует. Вычеркивание возможно.

Дальнейшие пробные вычеркивания выполняются аналогично.

В итоге получаем F_~= .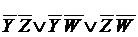

Рассмотрим еще один пример.

X	Y	Z	W	F~

Берем из D₁ первую конъюнкцию: 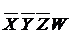и начинам ее укорачивать. Будем работать не с конъюнкциями, а с их кодами.

0 0 0 1
- 0 0 1	Все коды из D0 ортогональны
- - 0 1	Нельзя, так как в как в D0 есть код 0101
- 0 0 1	Восстанавливаем вычеркнутую переменную
- 0 - 1	Нельзя, так как в как в D0 есть код 0011
- 0 0 1	Восстанавливаем вычеркнутую переменную
- 0 0 -	Все коды из D0 ортогональны	Эта конъюнкция поглощает 0001 и 1001 из D1

Берем из D₁ следующую конъюнкцию: 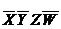и начинам ее укорачивать. Будем работать не с конъюнкциями, а с их кодами.

0 0 1 0
- 0 1 0	Все коды из D0 ортогональны
- - 1 0	Все коды из D0 ортогональны
- - - 0	Все коды из D0 ортогональны	Эта конъюнкция поглощает 0010 и 0110 из D1

Множество D₁ = Æ.

В результате получается F_~=