Для всех наборов значений переменных, на которых бф равна 1, выписываем характеристические функции единицы и объединяем их знаками дизъюнкции.
Данное аналитическое представление называется дизъюнктивной совершенной нормальной формой (ДСНФ).
Рассмотрим примеры ДСНФ.
| X | Y | F | F = X0Y1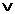 X1Y0 X1Y0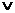 X1Y1= X1Y1= 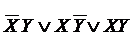 |
Основываясь на следствии из теоремы 1, в дснф можно вместо дизъюнкции использовать сумму по модулю два.
В результате получается формула, называемая полиномиальная совершенная нормальная форма (ПСНФ).
| X | Y | F | F = 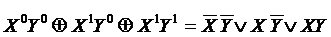 |
Конъюнктивная совершенная нормальная форма.
Введем в рассмотрение характеристическую функцию нуля 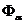 (Xn-1,…Xi,…X1,X0), которая равна 0 на наборе значений переменных (Xn-1,…Xi,…X1,X0), обозначенном a и равна 1 на всех остальных наборах.
(Xn-1,…Xi,…X1,X0), которая равна 0 на наборе значений переменных (Xn-1,…Xi,…X1,X0), обозначенном a и равна 1 на всех остальных наборах.
Теперь докажем следующую теорему.
Теорема 2.
Любая бф не равная константе 1 может быть представлена в виде
F(Xn-1, … Xi, … X1,X0) = 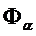 1&
1& 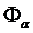 2&
2& 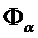 i =
i = 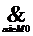
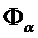 i,
i,
где M0 - множество всех номеров наборов значений переменных, на которых F(Xn-1,…Xi,…X1,X0) равна 0.
Доказательство:
Возьмем произвольный набор с номером a.
Пусть на этом наборе имеет место F(Xn-1,…X1,X0) = 1. Тогда правая часть равенства будет иметь вид 1&1&…&1=1, так как ни одна характеристическая функция не равна 0.
Следовательно, левая и правая части равны.
Если же на этом наборе F = 0, то правая часть будет иметь вид 1&1&…&0&…&1= 0, так как найдется одна 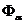 , принимающая значение 0.
, принимающая значение 0.
В результате мы получаем, что левая и правая части равны.
Рассмотрим метод получения характеристических функций нуля.
Xb =1 только в том случае, если значение Х равно значению b. Дизъюнкция степеней булевых переменных Xn-1,…Xi,…X1,X0 равна 0, если для всех Х значения степеней не равны значениям переменных. Отсюда вытекает правило получения характеристических функций нуля:
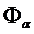 для набора значений переменных (bn-1…b1 b0) может быть представлена как дизъюнкция степеней переменных Xn-1,…X1,X0 со значениями степеней соответственно (1-bn-1) … (1-b1)(1-b0).
для набора значений переменных (bn-1…b1 b0) может быть представлена как дизъюнкция степеней переменных Xn-1,…X1,X0 со значениями степеней соответственно (1-bn-1) … (1-b1)(1-b0).
Рассмотрим пример.
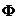 2(X,Y,Z,W)=F0010(X,Y,Z,W)= X1-0
2(X,Y,Z,W)=F0010(X,Y,Z,W)= X1-0 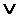 Y1-0
Y1-0 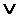 Z1-1
Z1-1 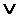 W1-0= X1
W1-0= X1 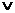 Y1
Y1 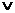 Z0
Z0 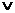 W1=
W1= 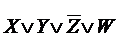
Зная как получать характеристические функции нуля, можно сформулировать еще один способ получения выражений в алгебре Буля для таблично заданных бф не равных константе «1»:
Для всех наборов значений переменных, на которых бф равна 0, выписываем характеристические функции нуля и объединяем их знаками конъюнкции.
Такое аналитическое представление называется конъюнктивной совершенной нормальной формой (КСНФ).
Таким образом, можно сделать следующий вывод:
FМ1= ДСНФ = 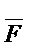 М0= КСНФ.
М0= КСНФ.
Действительно, основываясь на правилах булевой алгебры можно получить:
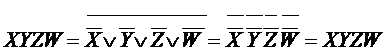
Решение о том, каким аналитическим представлением (ДСНФ или КСНФ) описывать булеву функцию принимается исходя из того, каких наборов меньше. Если М1 меньше, чем М0, то функцию лучше описывать с помощью ДСНФ, а если М0 меньше, чем М1, то с помощью КСНФ.
Рассмотрим пример КСНФ.
| X | Y | F | F = (X1-0 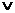 Y1-1)& (X1-1 Y1-1)& (X1-1 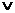 Y1-0)&( X1-1 Y1-0)&( X1-1 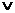 Y1-1)= = Y1-1)= = 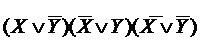 |
МИНИМИЗАЦИЯ БФ.
