Дизъюнктивная совершенная нормальная форма.
Введем в рассмотрение характеристическую функцию единицы Fa(Xn-1,…Xi,…X1,X0), которая равна 1 на наборе значений переменных (Xn-1,…Xi,…X1,X0), обозначенном a,и равна 0 на всех остальных наборах.
Наборы значений переменных удобно задавать по номерам, которые получаются при рассмотрении набора как двоичного числа.
Пример.
F2(X,Y,Z,W) – характеристическая функция единицы для набора значений переменных (X,Y,Z,W) с номером 2. (0010 = 2).
В таблице представлены функции F3 и F5 , которые принимают значение 1 на наборах №3 и 5, соответственно (отсчет начинается с набора №0).
| X | Y | Z | F3 | F5 |
Теорема 1.
Любая бф не равная константе 0 может быть представлена в виде
(Xn-1,…Xi,…X1,X0) = Fa1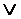 
Fa2 … 
Fa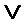i = 
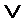Fai,при условии, что aiÎM1*, где M1* - множество всех номеров, на которых F(Xn-1,…Xi,…X1,X0) равна 1.
Доказательство:
Возьмем произвольный набор с номером a.
Пусть на этом наборе F(Xn-1,…X1,X0) = 1.
Тогда в правой части равенства найдется Fa(Xn-1, …Xi,…X1,X0) и правая часть будет иметь вид 1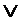
F, тоесть значения левой и правой части совпадают.
Если на наборе с номером a мы имеем F(Xn-1, …Xi,…X1,X0) = 0, то справа не будет Fa ,и правая часть будет иметь вид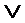 0
0 …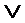
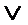0, то есть будет равна 0.
Таким образом, значения левой и правой части всегда совпадают.
Следствие.
Любая бф не равная константе 0 может быть представлена в виде
F(Xn-1,…Xi,…X1,X0) = 
Fai , где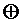 
- знак операции «сумма по модулю два».
| X | Y | 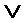 |  | Результаты операций «дизъюнкции» и «суммы по модулю два» совпадают, если X и Y одновременно не равны 1. |
Fa1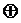 
Fa2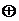 
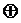... Fai =Fa1 
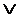Fa2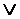 
... 
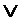Fai ,так как среди характеристических функций единицы Fai только одна принимает значение 1, а остальные равны нулю.
Замечание: Операция «сумма по модулю два» не является операцией алгебры Буля, но часто используется в булевых алгебрах с расширенным набором операций.
Рассмотрим процедуру получения характеристических функций единицы.
Если рассматривать bкак степень булевой переменной X, то
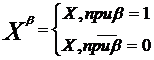
Т. е. Xb =1 только в том случае, если значение Х равно значению b.
Докажем это с помощью таблицы истинности.
| Х | b | Xb |
 | ||
 | ||
 | ||
 |
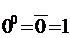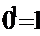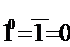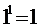Отсюда следует, что конъюнкция степеней булевых переменных Xn-1,…Xi,…X1, X0 равна 1, если для всех Х значения степеней равны значениям переменных. Поэтому конъюнкция переменных Xn-1, … X1, X0 со степенями, соответственно, an-1,...a1,a0 является характеристической функцией единицы для набора значений переменных an-1,...a1, a0.
Рассмотрим примеры характеристических функций.
Характеристическая функция единицы для набора №3 функции от трех переменных
F3(X,Y,Z) =F011(X,Y,Z)=X0&Y1&Z1=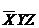 
Характеристическая функция единицы для набора №10 функции от четырех переменных
F10(X,Y,Z,W)=F1010(X,Y,Z,W)=X1Y0Z1W0=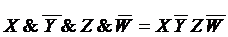 
Зная как построить характеристические функции единицы, можно на основании теоремы 1 сформулировать правило получения аналитической записи любой бф не равной константе 0: