Определитель верхней треугольной матрицы равен произведению диагональных элементов. A11 A22 Ann

Теорема (о разложении определителя по строке): определитель равен сумме произведений всех элементов какой-либо строки на их алгебраические дополнения. Это означает, что определитель матрицы n×n равен 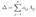(алгебраическое дополнение Aij=(-1)i+jMij. Здесь минор Mij - определитель получаемый из основного определителя вычеркиванием i-й строки и j-го столбца)

5.Обратная матрица

Обр матр — такая матр A^-1, при умн-и на кот исходная матрица A даёт в результате единичную матрицу E:

AA⁻¹ = A⁻¹A = E

Теорема : для того, чтобы для кв.м.А сущ-ла обр, дост-но чтобы опр-ль этой м. был отличен от 0.(Кв матр обратима тогда и только тогда, когда она невырожденная, т.е. её опр-ль не равен 0. Для некв матриц обр матриц не сущ-т.)

Доказательство:

Необходимость. Пусть для матрицы A существует обратная матрица A^-1.

detA^-1*A=detE => detA≠ 0.

Достаточность.

по м.А строим А^*

где А^* - м. алгебраических дополнений А^*

транспонируем полученную матрицу: (А^*)^Т=

найдем А* (А^*)^Т=С, Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,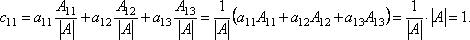

следовательно А* (А^*)^Т=detA*E => =>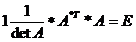

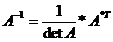
Сформ-м правило нах-я обр матр на примере матр А.

1. Находим опр-ль матр. Если Δ ≠0, то матр A^-1 сущ-т.

2. Составим матрицу A^* алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице A^* элементом i - ой строки и j - го столбца будет алгебраическое дополнение Aij элемента aij исх матрицы.

3. Транспонируем матрицу A^* и получим A^*T

4)

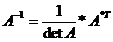
5 проверка A^-1*A=E

6.Минор к-го порядка матрицы. Базисный минор матр. Ранг матр и его св-ва. Теорема о ранге матр. Вычисление ранга.

А - прямоуг матрица размеров m*n.

Выбираем в матрице произвольные k строк и k столбцов. Элементы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка k. Определитель полученной матрицы называется минором k-го порядка матрицы А.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Наибольший из порядков миноров данной матрицы, отличный от нуля, называется рангом матрицы. (обозначается r(A))

нек. св-ва: 1) r(A)=0 => A=0

2)

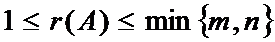
3) ранг верхней треугольной м. = числу диагональных эл-тов гл. диагонали неравных нулю.

ранг трапециевидной матрицы= числу диагональных эл-тов главного базисного минора.

Ранг матр не изменится от след преобр-й, наз элемент преобраз-ми матрицы

: - замены строк столбцами, а столбцов соответствующими строками; - перестановки строк матрицы; - вычеркивания строки, все элементы которой =0; - умножения строки на число, отличное от 0; - прибавления к эл-м строки соответствующих Эл-ов другой строки, умнож на одно и то же число. Ранг находят привидением её к треуг(трапециев) виду с пом этих элемент преобраз-ий

Теорема о ранге: наивысший порядок отличных от 0 миноров матрицы равен рангу этой матрицы

7. Критерий совместимости СЛАУ:

Теорема Кронекера-Капелли

Для того, чтобы СЛАУ, где AX=B, где матр A разм-ти m*n была совместной необх-мо и дост-но, чтобы ранг осн матр системы был равен рангу расшир матр системы.

r(A) = r(A/B)

Док-во:

Необходимость: пусть СЛАУ AX=B совместна.

Доказать, что ранги равны.

Сущ набор чисел (α1, α2…..αn), что будучи подставл в каждое из ур-й системы получим: