Матр А и В соглас-е, если число строк матр А равно числу столбцов матр В, и наоборот.

Оп-ция умн-я матриц определена только для соглас. матриц.

Кв матрицы одного и того же порядка и одной и той же размерности всегда согласованны.

Пусть задана матр А=aik i=1,m; k=1,n и матр В=bkj k=1,m; j=1,n. Тогда произв-ем А на В наз. матр С такая, что сik=ai1·b1k+ ai2·b2k +…+ ain·bnk, где i=1,m; k=1,n, т.е. эл-т i-той строки и k-того столбца матрицы произв-ия С равен ∑ произв-ий эл-ов i-той строки матр А на соответствующие эл-ты k-того столбца матр В.

Если выполняется равенство АВ=ВА, то матрицы А и В наз. перестановочными (коммутирующими)

Матр,получ. из данной заменой кажд ее строки столбц с тем же номером,наз. транспон-ой к данной.

Св-ва умножения:

1.А·(ВС)=(АВ)С

2. А(В+С)=АВ+ВС

3. (А+В)С=АС+ВС

4. α(АВ)=(αА)В

Св-ва транспонирования:

1.(А+В)^т=А^т+В^т

2. (АВ)^т=В·А^т

3. (А^т) ^т= А

Квадратная матрица А, которая не меняется при транспонировании, - симметричная.

Если матрица симметрична, то эл-ты, равноудаленные от главной диагонали, совпадают.

А= 2 5 -2

5 -7 3

-2 3 1

Опред-ль 1,2,3 порядков.

Квадратной матрице А порядка n можно сопоставить число det A, называемое ее определителем следующим образом:

1. n=1. A=(a₁); det A=a₁

2. n=2.

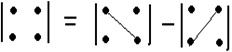
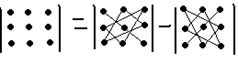
3. n=3.

Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: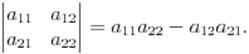

Определителем третьего порядка называется следующее выражение: 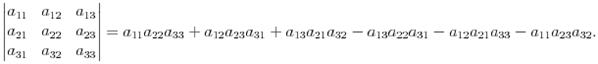Правило треугольников: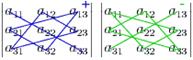

Пример: А= 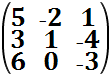det A= 5×1×(-3)+(-2)×(-4)×6+3×0×1- 6×1×1-3×(-2)×(-3)-0×(-4)×5=-15+48-6-18=9

3. Определитель квадратной матрицы порядка n.

Определитель квадратной матрицы n-ного порядка равен алгебраической сумме парных произведений элементов i-той строки матрицы А на их алгебраические дополнения или j-го столбца на их алгебраические дополнения.

Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения

4.Свойства определителей.

Если к.-л. строка или столбец в матрице состоит из одних нолей, то det

Этой матрицы равен 0

2)При транспонировании матрицы её определитель не изменяется: (detА =detА')

При перестановке местами 2-х строк или столбцов матрицы её

Определитель меняет свой знак на противоположный

Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0.

Если 2 строки или 2 столбца матрицы пропорциональны, то её det равен 0.

6) Определитель матрицы не изменяется если к элементам одной строки (или столбца) прибавить элементы другой строки (или столбца), умноженные на одно и то же число

Общий множитель строки или столбца можно выносить за знак определителя

8) Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,

Доказательство – проверкой.

9) det верхней треуг. матрицы = произведению диагональных эл-тов.

10) det A*B=detA*detB