Аналитическая геометрия в пространстве.
Плоскость.
1. Уравнение плоскости, проходящей через точку 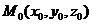 , перпендикулярно вектору
, перпендикулярно вектору 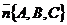 имеет вид:
имеет вид:
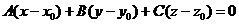 (1)
(1)
2. Общее уравнение плоскости:
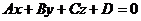 , (2)
, (2)
где 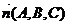 - нормальный вектор плоскости.
- нормальный вектор плоскости.
3. Уравнение плоскости в отрезках:
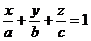 , (3)
, (3)
где a, b, c отрезки, отсекаемые плоскостью (3) на координатных осях Ox, Oy, Oz соответственно.
4. Уравнение плоскости, проходящей через три заданные точки 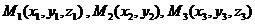 :
:
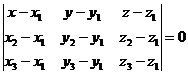 (4)
(4)
5. Углом между плоскостями 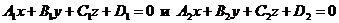 вычисляется по формуле:
вычисляется по формуле:
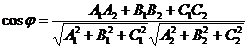 (5)
(5)
Условие параллельности плоскостей:
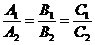 (6)
(6)
Условие перпендикулярности плоскостей :
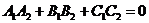 (7)
(7)
6. Расстояние d от точки 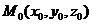 до плоскости
до плоскости 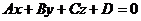 находится по формуле:
находится по формуле:
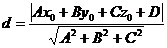 (8)
(8)
Прямая линия в пространстве.
1. Общее уравнение прямой:
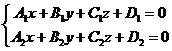 (9)
(9)
2. Уравнение прямой, проходящей через данную точку 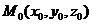 параллельно вектору
параллельно вектору 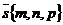 , имеет вид:
, имеет вид:
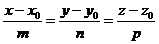 (10)
(10)
Уравнение (10) называется каноническим.
3. Пусть прямые заданы уравнениями:
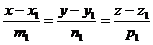 и
и 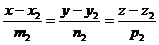 (11)
(11)
Тогда угол между этими прямыми определяется как угол между их направляющими векторами 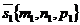 и
и 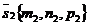 .
.
Угол между прямыми (16) определяется по формуле:
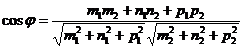 (12)
(12)
Условие параллельности прямых:
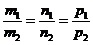 (13)
(13)
Условие перпендикулярности прямых:
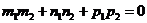 (14)
(14)
Прямая линия и плоскость в пространстве.
1. Угол между прямой 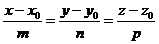 и плоскостью
и плоскостью 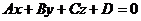 находится по формуле:
находится по формуле:
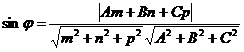 (15)
(15)
Условие параллельности прямой и плоскости:
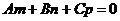 (16)
(16)
Условие перпендикулярности:
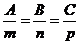 (17)
(17)
Для нахождения точки пересечения прямой и плоскости удобно воспользоваться параметрическими уравнениями прямой (12), тогда координаты точки пересечения находятся из системы уравнений:
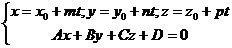 (18)
(18)
Примеры:
1. Даны точки 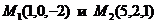 . Написать уравнение плоскости, проходящей через точку
. Написать уравнение плоскости, проходящей через точку 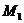 и перпендикулярно вектору
и перпендикулярно вектору 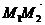 .
.
Решение:
Воспользуемся уравнением: 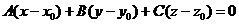 .
.
Нормальный вектор 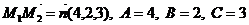 .
.
Следовательно, искомое уравнение имеет вид:
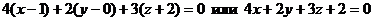
2. Написать уравнение прямой, проходящей через точку 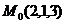 и перпендикулярно к прямым:
и перпендикулярно к прямым:
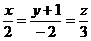 (1)
(1)
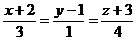 (2)
(2)
Решение:
Известны направляющие векторы прямых (1) и (2): 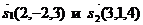 .
.
Поскольку искомая прямая перпендикулярна к прямым (1) и (2), то она перпендикулярна к векторам 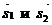 . Тогда за направляющий вектор
. Тогда за направляющий вектор  можно взять
можно взять 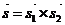 ,
,
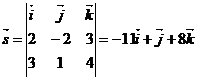
Уравнение искомой прямой имеет вид: 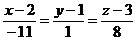 .
.
Задачи для самостоятельного решения.
1. Треугольник 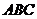 задан координатами своих вершин
задан координатами своих вершин 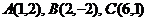 .
.
Требуется:
a) Написать уравнение стороны  ;
;
b) Написать уравнение высоты 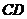 и вычислить ее длину;
и вычислить ее длину;
c) Найти угол между высотой 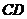 и медианой
и медианой 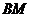 ;
;
2. Прямые 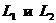 заданы уравнениями:
заданы уравнениями: 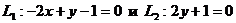 .
.
Найти:
a) Расстояние 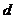 между прямимы;
между прямимы;
b) Точку пересечения прямых;
3. Написать уравнение плоскости P, проходящей через точки 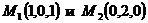 и параллельно вектору
и параллельно вектору 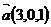 .
.
4. Написать канонические уравнения прямой, проходящей через точку 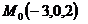 параллельно:
параллельно:
a) Вектору 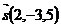 ;
;
b) Прямой 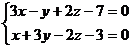 ;
;
c) Прямой 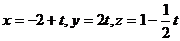 ;
;
5. Задана плоскость 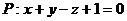 и прямая
и прямая 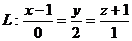 , причем
, причем 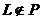 .
.
Вычислить:
a) 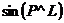 ;
;
b) координаты точки пересечения прямой и плоскости;
Пример решения типового расчета.
Задание №1.
Даны вершины 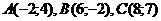 треугольника.
треугольника.
Найти:
1. длину стороны  ;
;
2. внутренний угол  в радианах с точностью до 0.001;
в радианах с точностью до 0.001;
3. уравнение высоты, проведенной через вершину 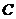 ;
;
4. уравнение медианы, проведенной через вершину 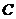 ;
;
5. точку пересечения высот треугольника;
6. длину высоты, опущенной из вершины 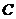 ;
;
7. систему линейных неравенств, определяющих внутреннюю область треугольника.
8. сделать чертеж;
Решение:
1. Расстояние между точками 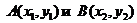 определяется на плоскости по формуле
определяется на плоскости по формуле
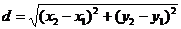 (1).
(1).
Тогда длина стороны  находится
находится 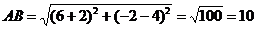 ,
, 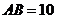 .
.
2. Угол 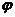 между прямыми, угловые коэффициенты которых равны
между прямыми, угловые коэффициенты которых равны 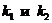 , вычисляются по формуле
, вычисляются по формуле
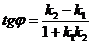 (2),
(2),
где 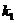 - угловой коэффициент
- угловой коэффициент  ,
, 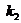 - угловой коэффициент
- угловой коэффициент 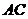 .
.
Найдем уравнение прямых  и
и 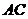 по формуле
по формуле
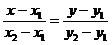 (3).
(3).
 :
: 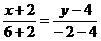
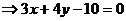 .
.
Чтобы найти угловой коэффициент запишем уравнение  в виде:
в виде: 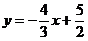 .
.
Значит 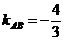 .
.
Уравнение прямой 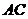 также находим по формуле (3).
также находим по формуле (3).
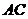 :
: 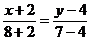
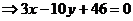 ;
; 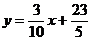 ;
; 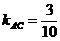 ;
;
Применяя формулу (2), имеем
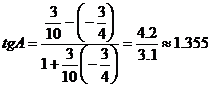
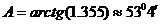 .
.
Используя таблицу перевода градусной меры в радианную, находим 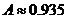 рад.
рад.
3.Запишем уравнение высоты, проведенной через точку 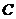 , используя уравнение прямой, проведенной по точке и направляющему вектору
, используя уравнение прямой, проведенной по точке и направляющему вектору  :
: 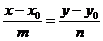 .
.
В качестве направляющего вектора  может быть выбран нормальный вектор прямой
может быть выбран нормальный вектор прямой  , т.е.
, т.е. 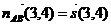 .
.
Уравнение высоты 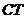 имеет вид:
имеет вид: 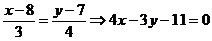 .
.
Аналогично найдем уравнение высоты 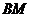 .
.
Направляющий вектор высоты 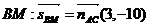 .
.
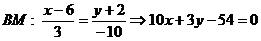
Из курса средней школы, известно, что три высоты пересекаются в одной точке. Чтобы найти точку пересечения высот 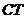 и
и 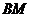 , нужно решить систему уравнений.
, нужно решить систему уравнений.
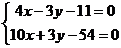
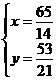 . Точка пересечения высот
. Точка пересечения высот 
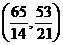 .
.
4. Известно, что медиана представляет отрезок, соединяющий вершину 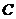 с серединой противоположной стороны (
с серединой противоположной стороны (  ). Найдем координаты середины отрезка
). Найдем координаты середины отрезка  по формулам:
по формулам:
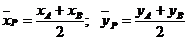 ;
;
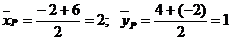
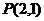 .
.
Уравнение медианы 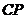 находим по формуле (3):
находим по формуле (3):
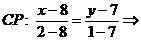
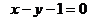 .
.
5. Длина высоты 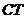 - расстояние от точки
- расстояние от точки 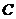 до прямой
до прямой  :
: 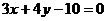 .
.
Воспользуемся формулой расстояния 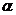 от точки
от точки 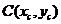 до прямой
до прямой 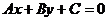
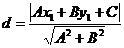
Получим 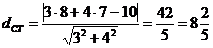 ед.
ед.
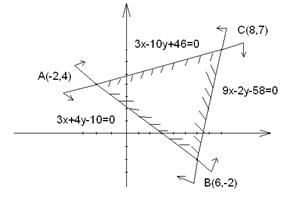
6. Запишем с помощью системы неравенств множество точек, лежащих внутри треугольника с вершинами 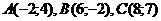 . Уравнения сторон треугольника:
. Уравнения сторон треугольника:
 :
: 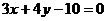
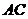 :
: 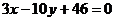
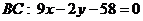
Множество внутренних точек можно рассматривать как пересечение трех полуплоскостей, из которых первая ограничена прямой  и содержит точку
и содержит точку 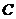 , вторая ограничена прямой
, вторая ограничена прямой 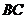 и содержит точку
и содержит точку  , третья ограничена прямой
, третья ограничена прямой 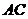 и содержит точку
и содержит точку 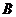 .
.
Подставим в левую часть уравнения  :
: 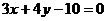 координаты точки
координаты точки 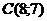 .
.
Получим 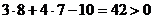 .
.
Следовательно, неравенство для первой полуплоскости будет 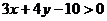 .
.
Найдем полуплоскость, ограниченную прямой 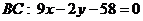 ,
, 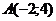 .
.
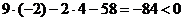
Второе неравенство: 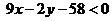 .
.
Аналогично находится третья полуплоскость. 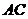 :
: 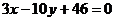 ,
, 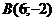 .
.
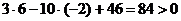
Третье неравенство: 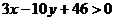 .
.
Таким образом, множество внутренних точек треугольника 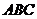 определяется системой неравенств:
определяется системой неравенств: 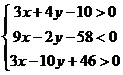 .
.
Задача №2.
Докажите, что векторы 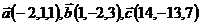 компланарны и найдите линейную зависимость между ними.
компланарны и найдите линейную зависимость между ними.
Решение:
Векторы компланарны тогда и только тогда, когда их смешанное произведение равно нулю.
Вычислим смешанное произведение векторов 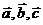 :
:
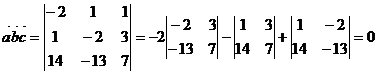
Следовательно данные векторы компланарны.
Компланарность означает их линейную зависимость. Найдем эту зависимость. Выразим векторы 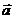 через векторы
через векторы 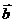 и
и 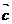 , т.е.
, т.е. 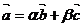 .
.
Запишем последнее равенство в координатах:
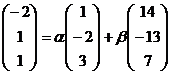 или
или 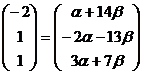
Из равенства матриц получили систему линейных уравнений:
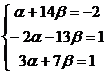
Решим эту систему методом Гаусса:
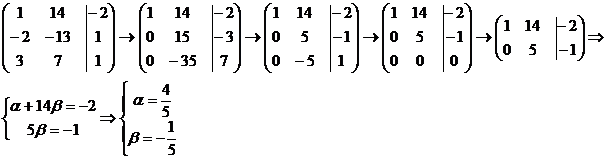
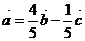 или
или 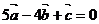 .
.
Ответ: 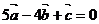 .
.
Задача №3.
Даны вершины пирамиды 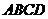 :
: 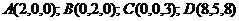 .
.
Найти:
1. длину ребра  ;
;
2. уравнение и площадь грани 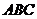 ;
;
3. уравнение и длину высоты, опущенной из вершины 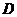 на грань
на грань 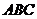 ;
;
4. угол между ребром 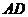 и гранью
и гранью 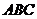 ;
;
5. объем пирамиды;
Решение:
1. Воспользуемся уравнением прямой в пространстве, проходящей через две точки 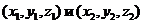 :
:
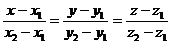 (1)
(1)
Подставим координаты точек 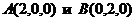 в (1), получим
в (1), получим
 :
: 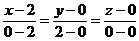
 :
: 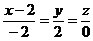 .
.
Длину ребра можно рассматривать как длину вектора 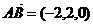 .
.
Длина вектора определяется по формуле: 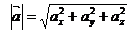 .
.
Тогда 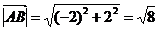 .
.
2. Площадь грани 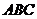 находим, используя векторное произведение
находим, используя векторное произведение 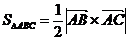
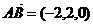 ;
; 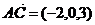
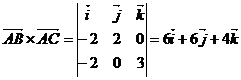
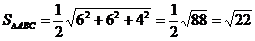
Уравнение грани представляет собой уравнение плоскости, проходящей через три точки:
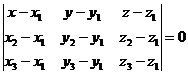 (2)
(2)
Подставляя в формулу (2) координаты точек 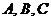 , получим
, получим
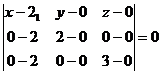
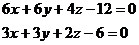 - уравнение грани
- уравнение грани 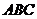 .
.
3. Уравнение высоты в данном случае представляет собой уравнение прямой в пространстве.
Используем каноническое уравнение прямой:
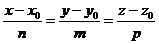 , (3)
, (3)
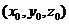 - координаты точки
- координаты точки 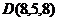 ,
,
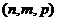 - координаты направляющего вектора прямой, которая перпендикулярна грани
- координаты направляющего вектора прямой, которая перпендикулярна грани 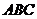 .
.
Следовательно, вектор нормали плоскости 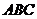 коллинеарен вектору высоты из вершины
коллинеарен вектору высоты из вершины 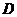 .
.
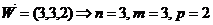
Уравнение высоты имеет вид:
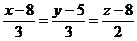
Длина высоты 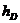 - расстояние от точки
- расстояние от точки 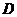 до плоскости
до плоскости 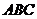 , воспользуемся формулой:
, воспользуемся формулой:
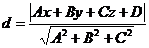
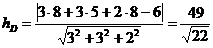 ед.
ед.
4. Угол между ребром 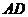 и гранью
и гранью 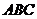 найдем как угол между векторами
найдем как угол между векторами 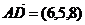 и
и 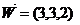 .
.
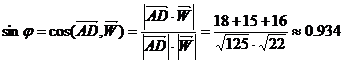
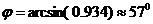
5. Объем пирамиды 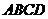 равен:
равен:
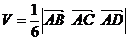
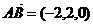 ;
; 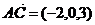 ;
; 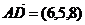
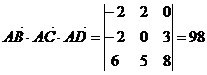
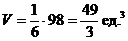
4.3. Типовой расчет:
Задача 1:Даны вершины 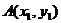 ,
, 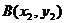 и
и 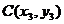 треугольника.
треугольника.
Найти:
1. длину стороны  ;
;
2. внутренний угол  в радианах с точностью до 0.001;
в радианах с точностью до 0.001;
3. уравнение высоты, проведенной через вершину 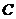 ;
;
4. уравнение медианы, проведенной через вершину 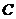 ;
;
5. точку пересечения высот треугольника;
6. длину высоты, опущенной из вершины 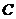 ;
;
7. систему линейных неравенств, определяющих внутреннюю область треугольника.
8. сделать чертеж;
1. 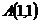 ,
, 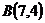 и
и 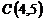 ;
;
2. 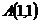 ,
, 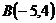 и
и 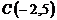 ;
;
3. 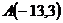 ,
, 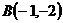 и
и 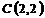 ;
;
4. 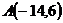 ,
, 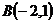 и
и 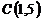 ;
;
5. 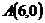 ,
, 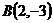 и
и 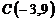 ;
;
6. 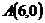 ,
, 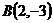 и
и 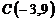 ;
;
7. 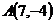 ,
, 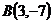 и
и 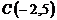 ;
;
8. 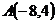 ,
, 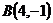 и
и 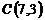 ;
;
9. 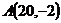 ,
, 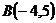 и
и 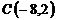 ;
;
10. 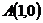 ,
, 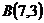 и
и 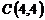 ;
;
11. 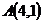 ,
, 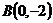 и
и 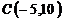 ;
;
12. 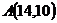 ,
, 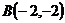 и
и 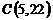 ;
;
13. 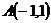 ,
, 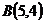 и
и 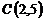 ;
;
14. 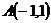 ,
, 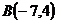 и
и 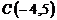 ;
;
15. 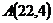 ,
, 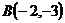 и
и 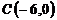 ;
;
16. 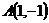 ,
, 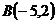 и
и 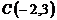 ;
;
17. 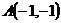 ,
, 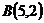 и
и 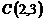 ;
;
18. 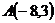 ,
, 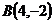 и
и 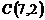 ;
;
19. 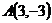 ,
, 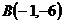 и
и 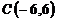 ;
;
20. 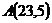 ,
, 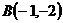 и
и 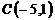 ;
;
21. 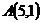 ,
, 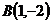 и
и 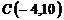 ;
;
22. 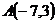 ,
, 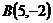 и
и 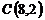 ;
;
23. 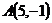 ,
, 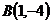 и
и 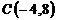 ;
;
24. 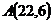 ,
, 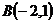 и
и 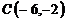 ;
;
25. 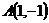 ,
, 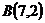 и
и 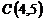 ;
;
26. 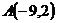 ,
, 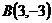 и
и 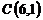 ;
;
27. 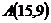 ,
, 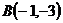 и
и 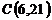 ;
;
28. 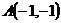 ,
, 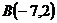 и
и 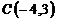 ;
;
29. 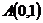 ,
,  и
и 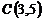 ;
;
30. 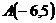 ,
, 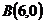 и
и 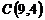 ;
;
Задача 2: Докажите, что векторы 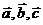 компланарны и найдите линейную зависимость между ними.
компланарны и найдите линейную зависимость между ними.
1. 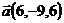 ,
, 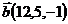 и
и 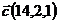 ;
;
2. 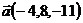 ,
, 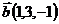 и
и 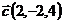 ;
;
3. 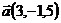 ,
, 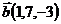 и
и 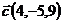 ;
;
4. 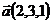 ,
, 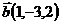 и
и 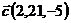 ;
;
5.  ,
, 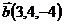 и
и 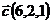 ;
;
6. 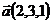 ,
, 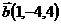 и
и 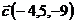 ;
;
7. 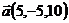 ,
, 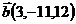 и
и 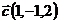 ;
;
8. 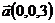 ,
, 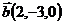 и
и 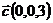 ;
;
9. 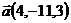 ,
, 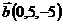 и
и 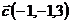 ;
;
10. 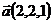 ,
, 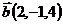 и
и 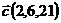 ;
;
11. 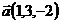 ,
, 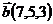 и
и 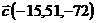 ;
;
12. 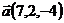 ,
, 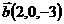 и
и 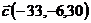 ;
;
13. 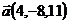 ,
, 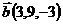 и
и 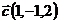 ;
;
14. 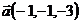 ,
, 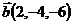 и
и 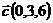 ;
;
15. 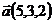 ,
, 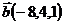 и
и 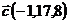 ;
;
16. 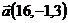 ,
, 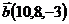 и
и 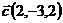 ;
;
17. 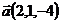 ,
, 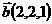 и
и 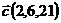 ;
;
18. 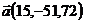 ,
, 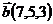 и
и 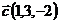 ;
;
19. 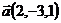 ,
, 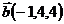 и
и 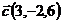 ;
;
20. 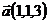 ,
, 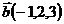 и
и 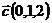 ;
;
21. 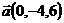 ,
, 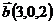 и
и 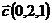 ;
;
22. 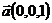 ,
, 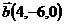 и
и 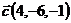 ;
;
23. 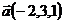 ,
, 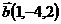 и
и 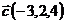 ;
;
24. 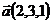 ,
, 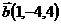 и
и 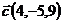 ;
;
25. 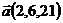 ,
, 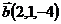 и
и 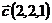 ;
;
26. 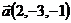 ,
, 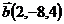 и
и 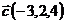 ;
;
27. 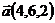 ,
, 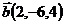 и
и 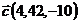 ;
;
28. 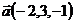 ,
, 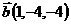 и
и 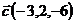 ;
;
29. 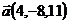 ,
, 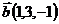 и
и 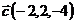 ;
;
30. 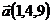 ,
, 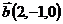 и
и 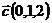 ;
;
Задача 3:
Найти:
1. длину ребра  ;
;
2. уравнение и площадь грани 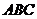 ;
;
3. уравнение и длину высоты, опущенной из вершины 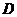 на грань
на грань 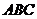 ;
;
4. угол между ребром 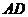 и гранью
и гранью 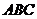 ;
;
5. объем пирамиды;
1. 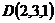 ,
, 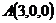 ,
, 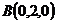 и
и 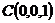 ;
;
2. 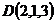 ,
, 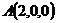 ,
, 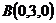 и
и 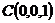 ;
;
3. 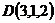 ,
, 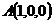 ,
, 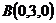 и
и 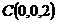 ;
;
4. 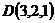 ,
, 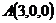 ,
, 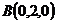 и
и 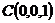 ;
;
5. 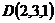 ,
, 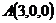 ,
, 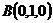 и
и 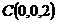 ;
;
6. 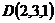 ,
, 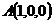 ,
, 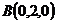 и
и 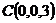 ;
;
7. 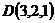 ,
, 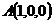 ,
, 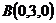 и
и 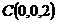 ;
;
8. 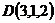 ,
, 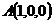 ,
, 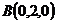 и
и 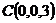 ;
;
9. 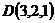 ,
, 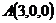 ,
, 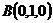 и
и 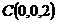 ;
;
10. 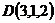 ,
, 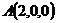 ,
, 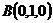 и
и 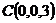 ;
;
11. 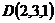 ,
, 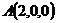 ,
, 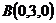 и
и 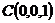 ;
;
12.  ,
, 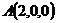 ,
, 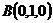 и
и 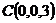 ;
;
13. 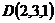 ,
, 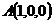 ,
, 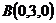 и
и 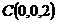 ;
;
14. 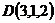 ,
, 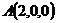 ,
, 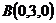 и
и 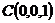 ;
;
15. 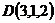 ,
, 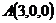 ,
, 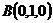 и
и 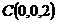 ;
;
16. 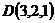 ,
, 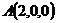 ,
, 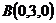 и
и 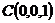 ;
;
17. 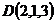 ,
, 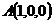 ,
, 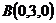 и
и 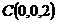 ;
;
18.  ,
, 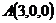 ,
, 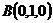 и
и 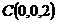 ;
;
19. 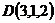 ,
, 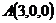 ,
, 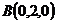 и
и 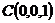 ;
;
20. 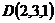 ,
, 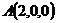 ,
, 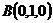 и
и 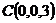 ;
;
21. 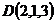 ,
, 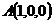 ,
, 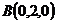 и
и 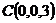 ;
;
22. 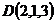 ,
, 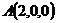 ,
, 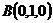 и
и 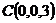 ;
;
23.  ,
, 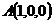 ,
, 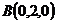 и
и 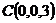 ;
;
24. 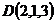 ,
, 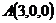 ,
, 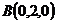 и
и 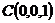 ;
;
25.  ,
, 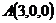 ,
, 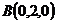 и
и 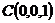 ;
;
26. 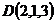 ,
, 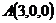 ,
, 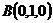 и
и 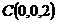 ;
;
27.  ,
, 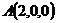 ,
, 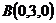 и
и 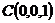 ;
;
28. 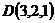 ,
, 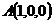 ,
, 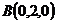 и
и 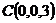 ;
;
29.  ,
, 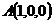 ,
, 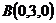 и
и 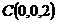 ;
;
30. 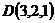 ,
, 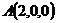 ,
,
