Плотность распределения непрерывной случайной величины

Числовые характеристики непрерывной случайной величины

№1

24.1.3./1

УС 1

АБ

Время: 1 мин.

Математическое ожидание М(Х) непрерывной случайной величины Х, заданной плотностью

распределения

f(x) = 0 при x≤2,

f(x) = 0,5при 2<x≤4,

f(x) = 0 при x>4,

равно…

+ 3

- 1/3

- 0

- 0,5

№2

24.1.3./2

УС 1

АБ

Время: 1 мин.

Дисперсия D(Х) непрерывной случайной величины Х, заданной плотностью распределения

f(x) = 0 при x≤2,

f(x) = 0,5при 2<x≤4,

f(x) = 0 при x>4,

равна…

+ 1/3

- 3

- 0

- 0,25

№3

24.1.3./3

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение σ(Х) непрерывной случайной величины Х, заданной плотностью распределения

f(x) = 0 при x≤2,

f(x) = 0,5при 2<x≤4,

f(x) = 0 при x>4,

равно…

+

-

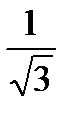
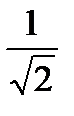
- 0,5

- 1/3

№4

24.1.3./4

УС 1

АБ

Время: 1 мин.

Математическое ожидание М(Х) непрерывной случайной величины Х, заданной плотностью

распределения

f(x) = 0 при x≤0,

f(x) = 2x при 0<x≤1,

f(x) = 0 при x>1,

равно…

+ 2/3

- 2

- 1/18

- 1

№5

24.1.3./5

УС 1

АБ

Время: 1 мин.

Дисперсия D(Х) непрерывной случайной величины Х, заданной плотностью распределения

f(x) = 0 при x≤0,

f(x) = 2x при 0<x≤1,

f(x) = 0 при x>1,

равна…

+ 1/18

- 4/9

- 2/3

- 2

№6

24.1.3./6

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение σ(Х) непрерывной случайной величины Х, заданной плотностью распределения

f(x) = 0 при x≤0,

f(x) = 2x при 0<x≤1,

f(x) = 0 при x>1,

равно…

+

-

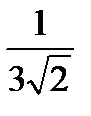
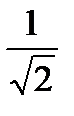
- 1/18

- 2/3

№7

24.1.3./7

УС 1

АБ

Время: 1 мин.

Математическое ожидание М(Х) непрерывной случайной величины Х, заданной функцией

распределения

F(x) = 0 при x≤0,

F(x) = x³при 0<x≤1,

F(x) = 1 при x>1,

равно…

+ 3/4

- 3/80

-

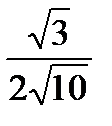
- 1

№8

24.1.3./8

УС 1

АБ

Время: 1 мин.

Дисперсия D(Х) непрерывной случайной величины Х, заданной плотностью распределения

F(x) = 0 при x≤0,

F(x) = x³при 0<x≤1,

F(x) = 1 при x>1,

равна…

+ 3/80

- 3/4

-

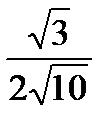
- 1

№9

24.1.3./9

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение σ(Х) непрерывной случайной величины Х, заданной плотностью распределения

F(x) = 0 при x≤0,

F(x) = x³при 0<x≤1,

F(x) = 1 при x>1,

равно…

+

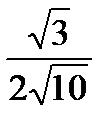
- 3/80

- 3/4

- 1

№10

24.1.3./10

УС 1

АБ

Время: 1 мин.

Математическое ожидание М(Х) непрерывной случайной величины Х, заданной функцией

распределения

F(x) = 0 при x≤0,

F(x) = x⁴ при 0<x≤1,

F(x) = 1 при x>1,

равно…

+ 4/5

- 2/75

-

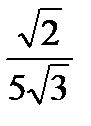
- 1

№11

24.1.3./11

УС 1

АБ

Время: 1 мин.

Дисперсия D(Х) непрерывной случайной величины Х, заданной плотностью распределения

F(x) = 0 при x≤0,

F(x) = x⁴ при 0<x≤1,

F(x) = 1 при x>1,

равна

+ 2/75

- 4/5

-

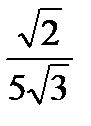
- 1

№12

24.1.3./12

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение σ(Х) непрерывной случайной величины Х, заданной плотностью распределения

F(x) = 0 при x≤0,

F(x) = x⁴ при 0<x≤1,

F(x) = 1 при x>1,

равно…

+

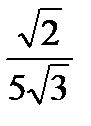
- 2/75

- 4/5

- 1

Виды распределений непрерывных случайных величин

Равномерное распределение

№1

24.2.1./1

УС 1

АБ

Время: 1 мин.

Плотность равномерного распределения f(x) непрерывной случайной величины X задается формулой…

+

-

-

-

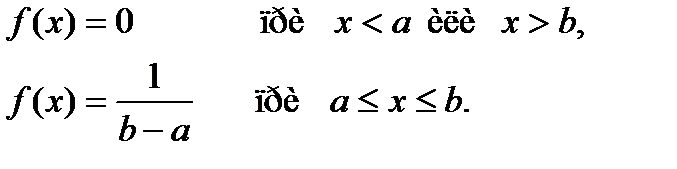
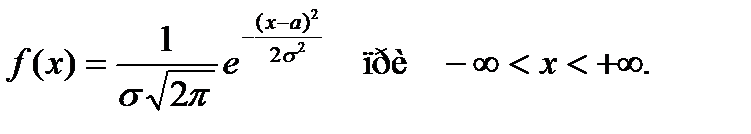
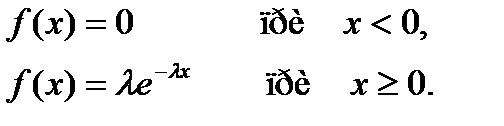
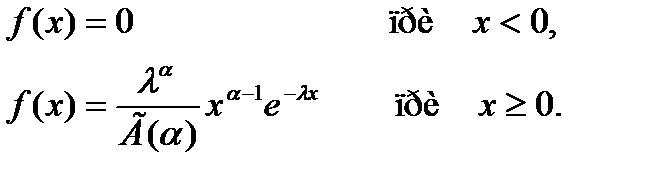
№2

24.2.1./2

УС 1

АБ

Время: 1 мин.

Функция равномерного распределения F(x) непрерывной случайной величины X задается формулой…

+

-

-

-

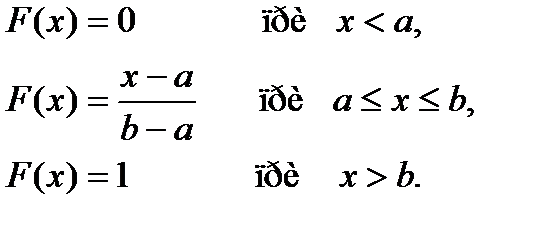
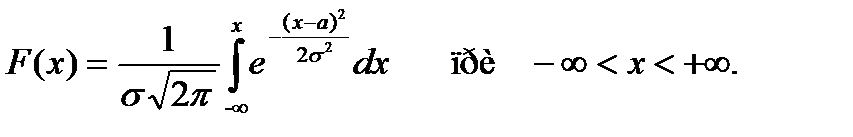
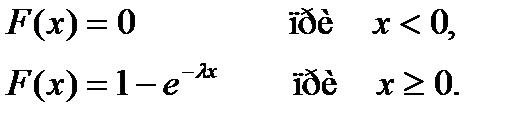
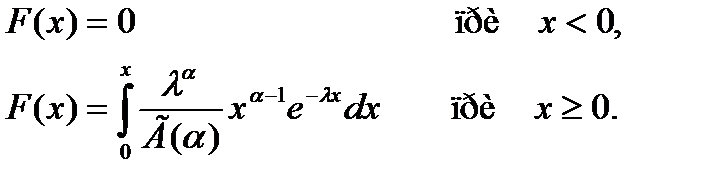
№3

24.2.1./3

УС 1

АБ

Время: 1 мин.

Число параметров, входящих в выражение плотности равномерного распределения f(x) непрерывной случайной величины X, равно…

+ 2

- 3

- 4

- 1

№4

24.2.1./4

УС 1

АБ

Время: 1 мин.

Вероятность того, что в результате испытания равномерно распределенная на отрезке [2;7] непрерывная случайная величина X примет значение, заключенное в интервале (3;5), равна…

+ 2/5

- 3/5

- 1

- 2/7

№5

24.2.1./5

УС 1

АБ

Время: 1 мин.

Вероятность того, что в результате испытания равномерно распределенная на отрезке [1;9] непрерывная случайная величина X примет значение, заключенное в интервале (2;4), равна…

+ 1/4

- 1/2

- 1

- 1/9

№6

24.2.1./6

УС 1

АБ

Время: 1 мин.

Вероятность того, что в результате испытания равномерно распределенная на отрезке [3;8] непрерывная случайная величина X примет значение, заключенное в интервале (3;6), равна…

+ 3/5

- 1/2

- 1

- 3/8

№7

24.2.1./7

УС 1

АБ

Время: 1 мин.

Вероятность того, что в результате испытания равномерно распределенная на отрезке [1;6] непрерывная случайная величина X примет значение, заключенное в интервале (4;5), равна…

+ 1/5

- 4/5

- 1

- 1/6

№8

24.2.1./8

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, равномерно распределенной на отрезке [-3;1], равно…

+ -1

- -2

- -3

- 1

№9

24.2.1./9

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, равномерно распределенной на отрезке [1;15], равно…

+ 8

- 7

- 1

- 15

№10

24.2.1./10

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, равномерно распределенной на отрезке [-1;5], равно…

+ 2

- 3

- -1

- 5

№11

24.2.1./11

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, равномерно распределенной на отрезке [2;10], равно…

+ 6

- 4

- 2

- 10

№12

24.2.1./12

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, равномерно распределенной на отрезке [10;16], равно…

+ 13

- 3

- 10

- 16

№13

24.2.1./13

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, равномерно распределенной на отрезке [-3;1], равна…

+ 4/3

- 16

- 8

- 4

№14

24.2.1./14

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, равномерно распределенной на отрезке [1;13], равна…

+ 12

- 144

- 170

- 14

№15

24.2.1./15

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, равномерно распределенной на отрезке [2;10], равна…

+ 16/3

- 64

- 6

- 16

№16

24.2.1./16

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, равномерно распределенной на отрезке [4;16], равна…

+ 12

- 272

- 144

- 100

№17

24.2.1./17

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, равномерно распределенной на отрезке [-1;5], равна…

+ 3

- 36

- 26

- 2

№18

24.2.1./18

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, равномерно распределенной на отрезке [-3;1], равно…

+

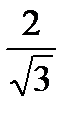
- 4

-

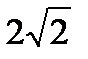
- 2

№19

24.2.1./19

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, равномерно распределенной на отрезке [1;13], равна…

+

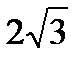
- 12

-

-

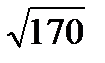
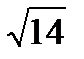
№20

24.2.1./20

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, равномерно распределенной на отрезке [2;10], равна…

+

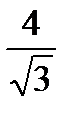
- 8

-

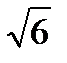
- 4

№21

24.2.1./21

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, равномерно распределенной на отрезке [4;16], равна…

+

-

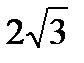
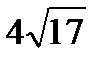
- 12

- 10

№22

24.2.1./22

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, равномерно распределенной на отрезке [-1;5], равна…

+

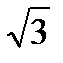
- 6

-

-

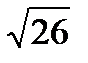
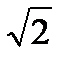
№23

24.2.1./23

УС 1

АБ

Время: 1 мин.

Вероятность P(X<5) непрерывной случайной величины X, равномерно распределенной на отрезке [2;7], равна…

+ 0,6

- 0,4

- 0,1

- 0,2

№24

24.2.1./24

УС 1

АБ

Время: 1 мин.

Вероятность P(X>4) непрерывной случайной величины X, равномерно распределенной на отрезке [-5;15], равна…

+ 0,55

- 0,45

- 0,6

- 0,2

№25

24.2.1./25

УС 1

АБ

Время: 1 мин.

Вероятность P(1>X>4) непрерывной случайной величины X, равномерно распределенной на отрезке [0;10], равна…

+ 0,3

- 0,1

- 0,6

- 0,7

Нормальное распределение

№1

24.2.2./1

УС 1

АБ

Время: 1 мин.

Плотность нормального распределения f(x) непрерывной случайной величины X задается формулой…

-

+

-

-

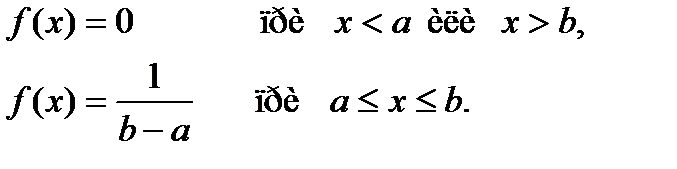
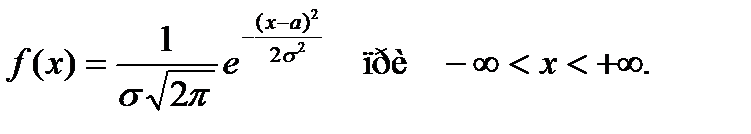
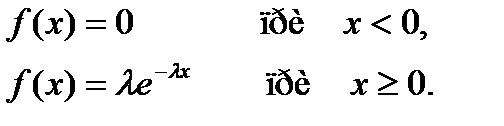
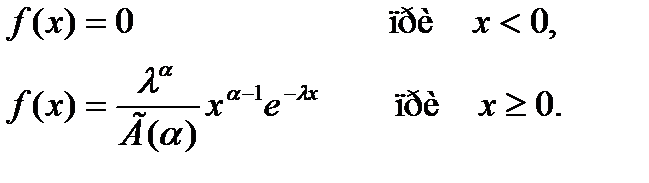
№2

24.2.2./2

УС 1

АБ

Время: 1 мин.

Функция нормального распределения F(x) непрерывной случайной величины X задается формулой…

-

+

-

-

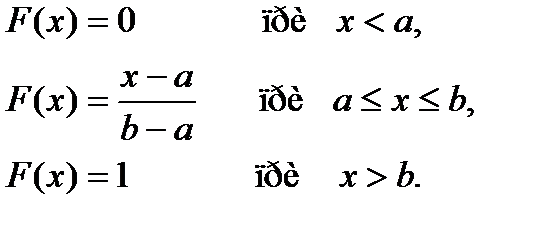
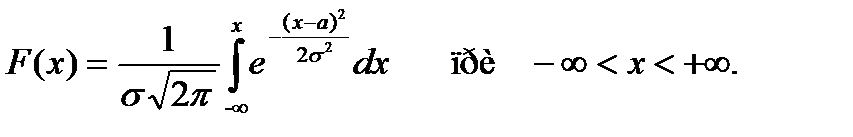
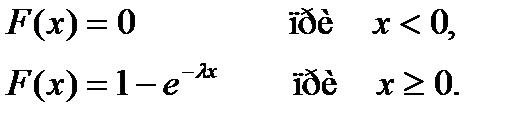
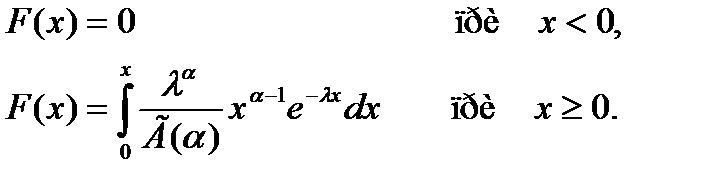
№3

24.2.2./3

УС 1

АБ

Время: 1 мин.

Число параметров, входящих в выражение плотности нормального распределения f(x) непрерывной случайной величины X, равно…

+ 2

- 3

- 4

- 1

№4

24.2.2./4

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

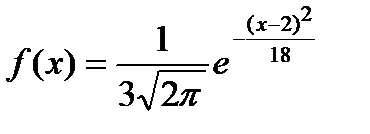
равно…

+ 2

- 3

- 9

- 18

№5

24.2.2./5

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

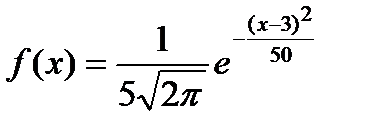
равно…

+ 3

- 5

- 25

- 50

№6

24.2.2./6

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

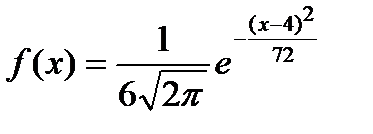
равно…

+ 4

- 6

- 36

- 72

№7

24.2.2./7

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

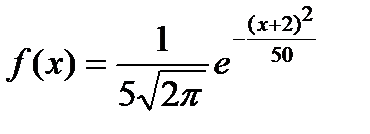
равно…

+ -2

- 5

- 25

- 50

№8

24.2.2./8

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

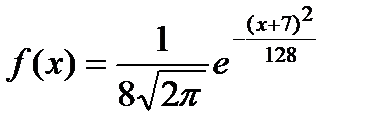
равно…

+ -7

- 8

- 64

- 128

№9

24.2.2./9

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

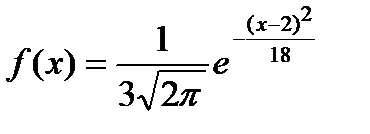
равно…

+ 9

- 2

- 3

- 18

№10

24.2.2./10

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

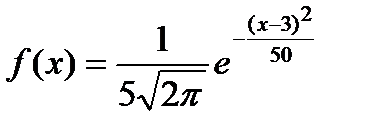
равно…

+ 25

- 3

- 5

- 50

№11

24.2.2./11

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

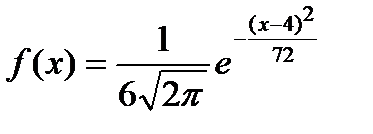
равно…

+ 36

- 6

- 4

- 72

№12

24.2.2./12

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

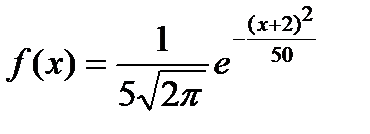
равно…

+ 25

- 5

- -2

- 50

№13

24.2.2./13

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

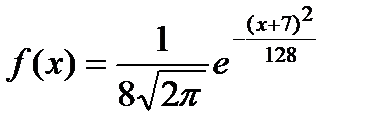
равно…

+ 64

- 8

- -7

- 128

№14

24.2.2./14

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

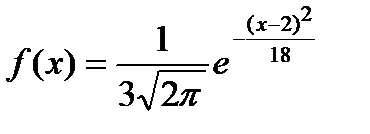
равно…

+ 3

- 3

- 2

- 18

№15

24.2.2./15

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

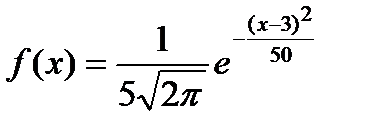
равно…

+ 5

- 3

- 25

- 50

№16

24.2.2./16

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

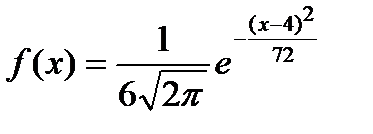
равно…

+ 6

- 4

- 36

- 72

№17

24.2.2./17

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

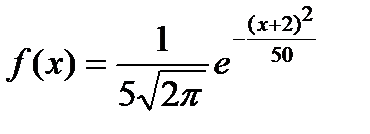
равно…

+ 5

- -2

- 25

- 50

№18

24.2.2./18

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, нормально распределенной с плотностью вероятности

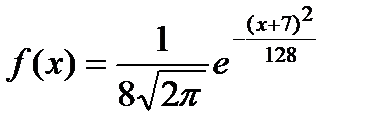
равно…

+ 8

- -7

- 64

- 128

Показательное распределение

№1

24.2.3./1

УС 1

АБ

Время: 1 мин.

Плотность показательного распределения f(x) непрерывной случайной величины X задается формулой…

+

-

-

-

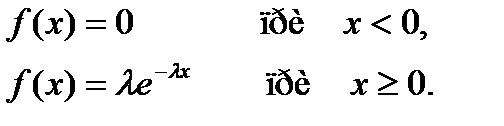
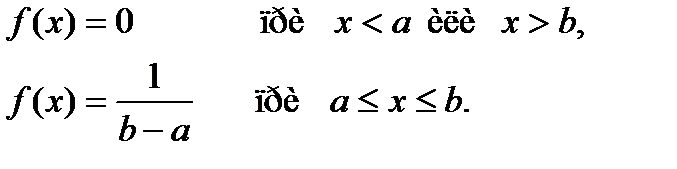
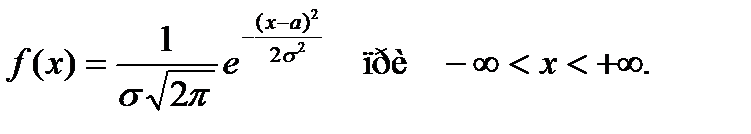
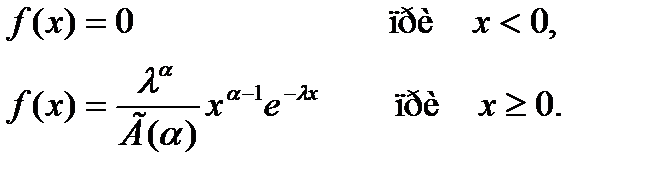
№2

24.2.3./2

УС 1

АБ

Время: 1 мин.

Функция показательного распределения F(x) непрерывной случайной величины X задается формулой…

+

-

-

-

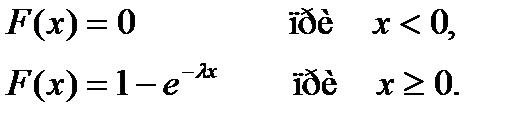
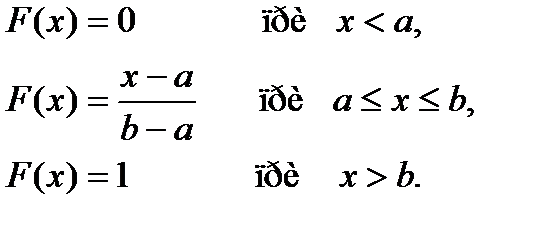
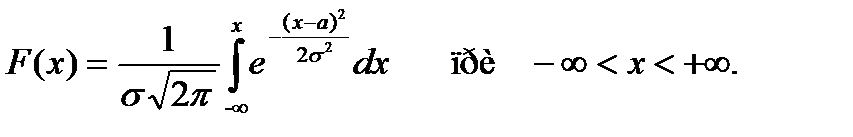
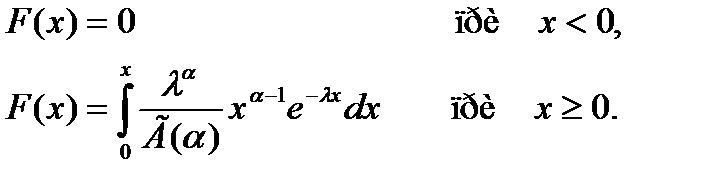
№3

24.2.3./3

УС 1

АБ

Время: 1 мин.

Число параметров, входящих в выражение плотности показательного распределения f(x) непрерывной случайной величины X, равно…

+ 1

- 2

- 3

- 4

№4

24.2.3./4

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

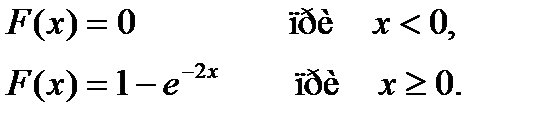
равно…

+ 0,5

- 2

- -2

- -0,5

№5

24.2.3./5

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

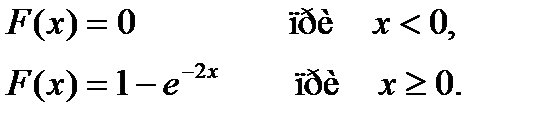
равно…

+ 0,5

- 2

- -2

- -0,5

№6

24.2.3./6

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

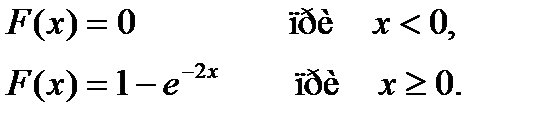
равна…

+ 0,25

- 4

- -2

- -0,25

№7

24.2.3./7

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

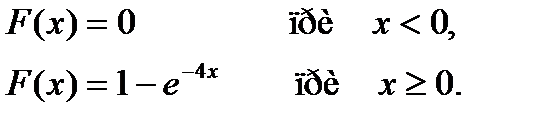
равно…

+ 0,25

- 4

- -4

- -0,25

№8

24.2.3./8

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

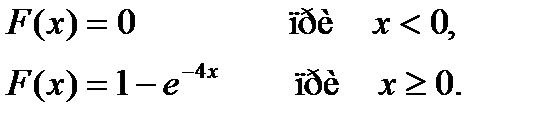
равно…

+ 0,25

- 4

- -4

- -0,25

№9

24.2.3./9

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

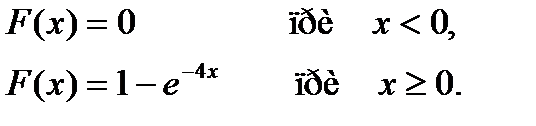
равна…

+ 0,0625

- 16

- -4

- -0,0625

№10

24.2.3./10

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

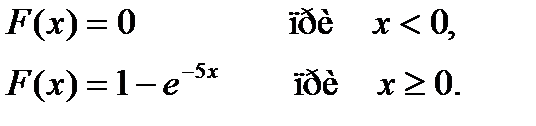
равно…

+ 0,2

- 5

- -5

- -0,2

№11

24.2.3./11

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

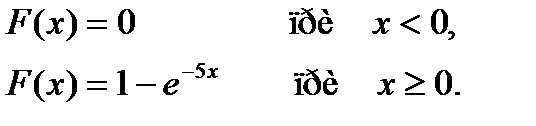
равно…

+ 0,2

- 5

- -5

- -0,2

№12

24.2.3./12

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

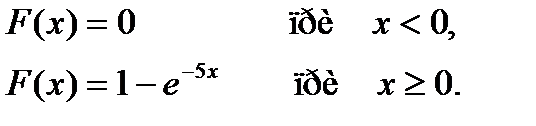
равна…

+ 0,04

- 25

- -5

- -0,04

№13

24.2.3./13

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

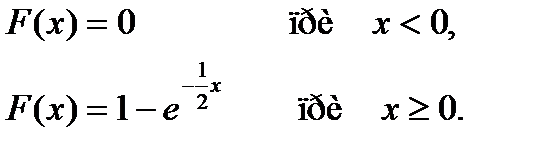
равно…

+ 2

- 0,5

- -0,5

- -2

№14

24.2.3./14

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

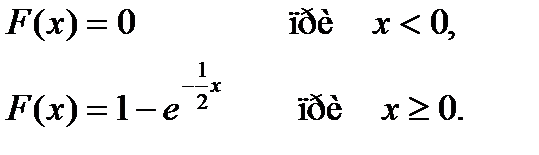
равно…

+ 2

- 4

- -0,5

- -2

№15

24.2.3./15

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

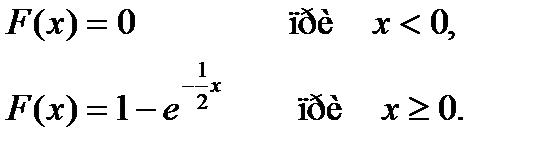
равна…

+ 4

- 0,25

- -0,5

- -4

№16

24.2.3./16

УС 1

АБ

Время: 1 мин.

Математическое ожидание непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

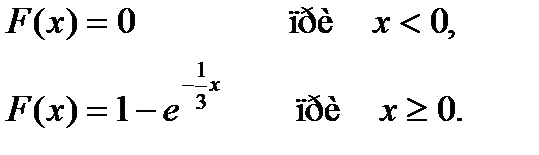
равно…

+ 3

- 1/3

- -1/3

- -3

№17

24.2.3./17

УС 1

АБ

Время: 1 мин.

Среднее квадратическое отклонение непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

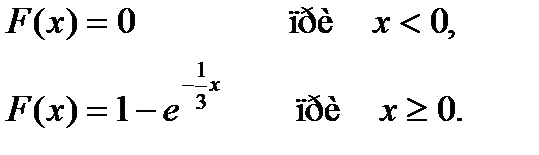
равно…

+ 3

- 1/3

- -1/3

- -3

№18

24.2.3./18

УС 1

АБ

Время: 1 мин.

Дисперсия непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

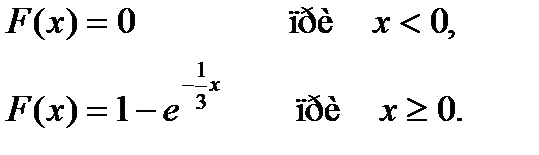
равна…

+ 9

- 1/9

- -1/3

- -9

№19

24.2.3./19

УС 1

АБ

Время: 1 мин.

Вероятность попадания в интервал (2;6) непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

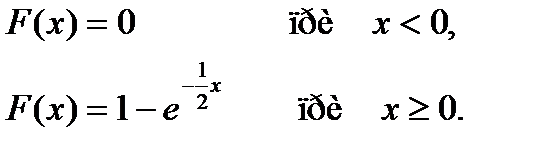
равна…

+

-

-

-

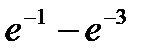
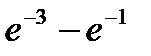
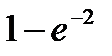
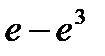
№20

24.2.3./20

УС 1

АБ

Время: 1 мин.

Вероятность попадания в интервал (2;8) непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

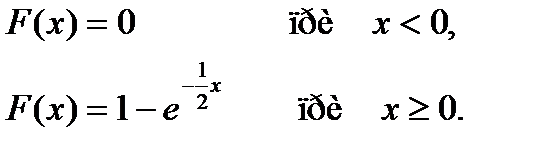
равна…

+

-

-

-

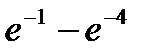
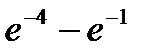
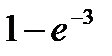
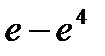
№21

24.2.3./21

УС 1

АБ

Время: 1 мин.

Вероятность попадания в интервал (3;9) непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

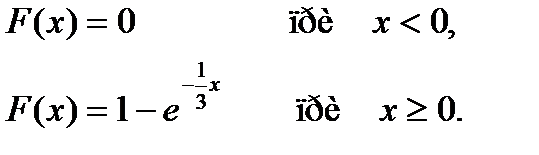
равна…

+

-

-

-

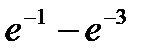
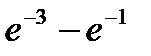
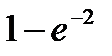
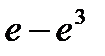
№22

24.2.3./22

УС 1

АБ

Время: 1 мин.

Вероятность попадания в интервал (1;5) непрерывной случайной величины Х, распределенной по показательному закону с функцией распределения

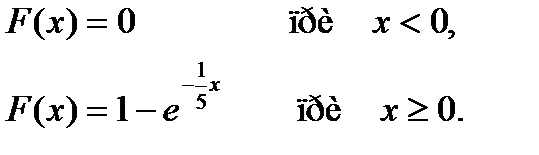
равна…

+

-

-

-

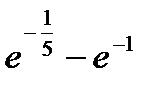
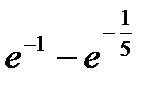
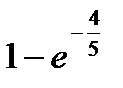
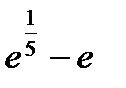
№23

24.2.3./23

УС 1

АБ

Время: 1 мин.

Вероятность попадания в интервал (2;6) непрерывной случайной величины Х, распределенной по показательному закону с математическим ожиданием М(х) = 2, равна…

+

-

-

-

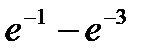
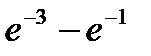
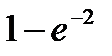
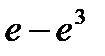
№24

24.2.3./24

УС 1

АБ

Время: 1 мин.

Вероятность попадания в интервал (2;8) непрерывной случайной величины Х, распределенной по показательному закону с дисперсией D(x) = 4, равна…

+

-

-

-

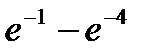
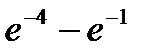
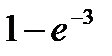
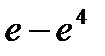
№25

24.2.3./25

УС 1

АБ

Время: 1 мин.

Вероятность попадания в интервал (3;9) непрерывной случайной величины Х, распределенной по показательному закону со средним квадратическим отклонением σ(х) = 3, равна…

+

-

-

-

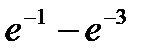
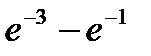
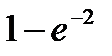
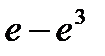
№1

25.1.1./1

УС 1

АБ

Время: 1 мин.

Задачи математической статистики:

+ оценка неизвестной вероятности события

+ оценка неизвестной функции распределения

+ оценка параметров распределения, вид которого известен

- изучение алгебры событий

- доказательство теорем сложения и умножения вероятностей

№2

25.1.1./2

УС 1

АБ

Время: 1 мин.

Задачи математической статистики:

+ указать способы сбора и группировки статистических сведений, полученных в результате наблюдений

+ оценка зависимости случайной величины от других случайных величин

+ проверка статистических гипотез о виде неизвестного распределения

+ оценка параметров распределения, вид которого известен

- вычисление вероятности случайного события

- доказательство формулы полной вероятности

№3

25.1.1./3

УС 1

АБ

Время: 1 мин.

Выборка, адекватно отражающая исследуемую генеральную совокупность, называется…

+ репрезентативной

+ представительной

- наивероятнейшей

- единичной

- однотипной

№4

25.1.1./4

УС 1

АБ

Время: 1 мин.

Число объектов статистической совокупности называется ее…

+ объемом

- шириной

- высотой

- площадью

- глубиной

№5

25.1.1.5

УС 1

АБ

Время: 1 мин.

Ограниченная совокупность случайно отобранных объектов из всей совокупности называется…

+ выборкой

+ выборочной совокупностью

- генеральной совокупностью

- повторной выборкой

- статистическим рядом

№6

25.1.1.6

УС 1

АБ

Время: 1 мин.

Вся совокупность объектов, из которых производится выборка, называется…

+ генеральной совокупностью

- выборочной совокупностью

- общей совокупностью

- бесповторной выборкой

- статистическим рядом

Способы отбора

№1

25.1.2./1

УС 1

АБ

Время: 1 мин.

Выборка, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность, называется…

+ повторной

- бесповторной

- возвратной

- восполнимой

№2

25.1.2./2

УС 1

АБ

Время: 1 мин.

Выборка, при которой отобранный объект (перед отбором следующего) не возвращается в генеральную совокупность, называется…

+ бесповторной

- повторной

- невозвратной

- невосполнимой

№3

25.1.2./3

УС 1

АБ

Время: 1 мин.

Отбор, не требующий разбиения генеральной совокупности на части:

+ простой случайный бесповторный

+ простой случайный повторный

- типический

- механический

- серийный

№4

25.1.2./4

УС 1

АБ

Время: 1 мин.

Отбор, при котором генеральная совокупность разбивается на части:

+ типический

+ механический

+ серийный

- простой случайный бесповторный

- простой случайный повторный

№5

25.1.2./5

УС 1

АБ

Время: 1 мин.

Отбор, при котором объекты извлекают по одному из всей генеральной совокупности, называется…

+ простым случайным

- типическим

- механическим

- серийным

№6

25.1.2./6

УС 1

АБ

Время: 1 мин.

Отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее типической части, называется…

+ типическим

- простым случайным

- механическим

- серийным

№7

25.1.2./7

УС 1

АБ

Время: 1 мин.

Отбор, при котором генеральную совокупность механически делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект, называется…

+ механическим

- типическим

- простым случайным

- серийным

№8

25.1.2./8

УС 1

АБ

Время: 1 мин.

Отбор, при котором объекты отбирают из генеральной совокупности не по одному, а сериями, которые подвергаются сплошному обследованию, называется…

+ серийным

- простым случайным

- типическим

- механическим

Вариационные ряды

Статистическая гипотеза

№1

26.2.1./1

УС 1

АБ

Время: 1 мин.

Статистическими являются гипотезы:

+ генеральная совокупность распределена по закону Пуассона

+ генеральная совокупность распределена по нормальному закону

+ дисперсии двух нормальных генеральных совокупностей равны между собой

- на Марсе есть жизнь

- сегодня вечером будет дождь

№2

26.2.1./2

УС 1

АБ

Время: 1 мин.

Статистическими являются гипотезы:

+ генеральная совокупность распределена по показательному закону

+ генеральная совокупность распределена по нормальному закону

+ математические ожидания двух нормальных генеральных совокупностей равны между собой

- на Венере есть жизнь

- завтра утром будет дождь

№3

26.2.1./3

УС 1

АБ

Время: 1 мин.

Альтернативной для основной гипотезы Н₀: М(Х)=12 может быть…

+ Н₁: М(Х)≠12

- Н₁: М(Х)>12

- Н₁: М(Х)<12

- Н₁: М(Х)≥12

- Н₁: М(Х)≤12

№4

26.2.1./4

УС 1

АБ

Время: 1 мин.

Альтернативной для основной гипотезы Н₀: М(Х)=15 может быть…

+ Н₁: М(Х)≠15

- Н₁: М(Х)>15

- Н₁: М(Х)<15

- Н₁: М(Х)≥15

- Н₁: М(Х)≤15

№5

26.2.1./5

УС 1

АБ

Время: 1 мин.

Альтернативной для основной гипотезы Н₀: D(Х)=5 может быть…

+ Н₁: D(Х)≠5

- Н₁: D(Х)>5

- Н₁: D(Х)<5

- Н₁: D(Х)≥5

- Н₁: D(Х)≤5

№6

26.2.1./6

УС 1

АБ

Время: 1 мин.

Альтернативной для основной гипотезы Н₀: D(Х)=9 может быть…

+ Н₁: D(Х)≠9

- Н₁: D(Х)>9

- Н₁: D(Х)<9

- Н₁: D(Х)≥9

- Н₁: D(Х)≤9

Элементы теории корреляции

Плотность распределения непрерывной случайной величины

Плотность распределения f(x) и функция распределения F(x) непрерывной случайной величины X связаны формулой:

+ f(x) = F'(x)

+

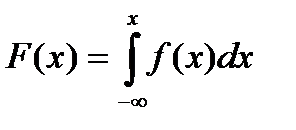
- F(x) = f '(x)

-

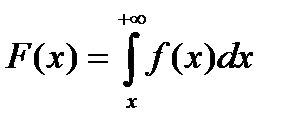
- f(x) = F(x) + C

Плотность распределения f(x) непрерывной случайной величины X есть функция…

+ неотрицательная

- неположительная

- знакопеременная

- отрицательная

- положительная

Несобственный интеграл 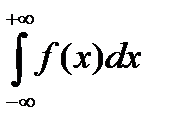от плотности распределения f(x) непрерывной случайной величины равен…

+ единице

- нулю

- функции распределения F(x)

- не существует

Вероятность P того, что непрерывная случайная величина X с плотностью распределения f(x) примет значение, принадлежащее интервалу (a,b), определяется равенством…

+

-

-

-

-

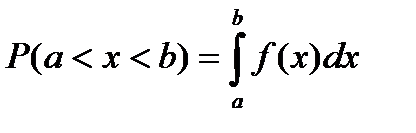
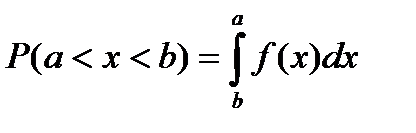
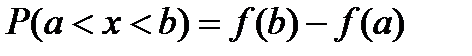
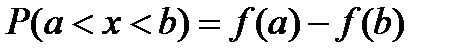
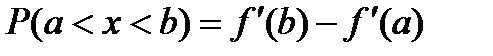
Значение функции распределения F(π/3) при заданной плотности распределения f(x) непрерывной случайной величины X

f(x) = 0 при x≤0,

f(x) = sinx при 0<x≤π/2,

f(x) = 0 при x> π/2,

равно…

+ 1/2

-

-

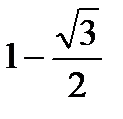
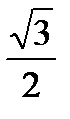
- 0

Значение функции распределения F(π/6) при заданной плотности распределения f(x) непрерывной случайной величины X

f(x) = 0 при x≤0,

f(x) = sinx при 0<x≤π/2,

f(x) = 0 при x> π/2,

равно…

+

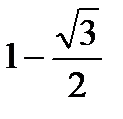
- 1/2

-

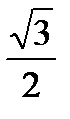
- 0

Значение функции распределения F(π) при заданной плотности распределения f(x) непрерывной случайной величины X

f(x) = 0 при x≤0,

f(x) = sinx при 0<x≤π/2,

f(x) = 0 при x> π/2,

равно…

+ 1

- 1/2

- 2

- 0

Значение функции распределения F(3/4) при заданной плотности распределения f(x) непрерывной случайной величины X

f(x) = 0 при x≤1,

f(x) = x – 1/2при 1<x≤2,

f(x) = 0 при x>2,

равно…

+ 0

- 1/4

- 3/32

- 1

Значение функции распределения F(3) при заданной плотности распределения f(x) непрерывной случайной величины X

f(x) = 0 при x≤1,

f(x) = x – 1/2при 1<x≤2,

f(x) = 0 при x>2,

равно…

+ 1

- 5/2

- 2/5

- 0

Значение функции распределения F(3/2) при заданной плотности распределения f(x) непрерывной случайной величины X

f(x) = 0 при x≤1,

f(x) = x – 1/2при 1<x≤2,

f(x) = 0 при x>2,

равно…

+ 3/8

- 3/4

- 0

- 1

Значение плотности распределения f(π/6) при заданной функции распределения F(x) непрерывной случайной величины X

F(x) = 0 при x≤0,

F(x) = sinx при 0<x≤π/2,

F(x) =1 при x> π/2,

равно…

+

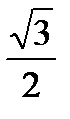
- 1/2

- 1

- 0

Значение плотности распределения f(π/3) при заданной функции распределения F(x) непрерывной случайной величины X

F(x) = 0 при x≤0,

F(x) = sinx при 0<x≤π/2,

F(x) =1 при x> π/2,

равно…

+ 1/2

-

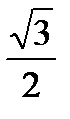
- 1

- 0

Значение плотности распределения f(π) при заданной функции распределения F(x) непрерывной случайной величины X

F(x) = 0 при x≤0,

F(x) = sinx при 0<x≤π/2,

F(x) =1 при x> π/2,

равно…

+ 0

- 1/2

- 1

- -1

№14

24.1.2./14

УС 1

АБ

Время: 1 мин.

Значение плотности распределения f(-π/4) при заданной функции распределения F(x) непрерывной случайной величины X

F(x) = 0 при x≤0,

F(x) = sinx при 0<x≤π/2,

F(x) =1 при x> π/2,

равно…

+ 0

-

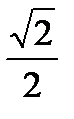
- 1

-

 <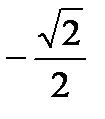