Указания о порядке выполнения контрольных работ

Каждый студент-заочник согласно учебному плану, в пятом семестре выполняет две контрольные работы. В первую контрольную работу входят задачи 1 и 2, во вторую – 3 и 4. В шестом семестре также выполняются две контрольные работы (3 и 4). В третью контрольную работу входят задачи 5 и 6, в четвертую – 7 и 8.

Исходные данные для решения задач выбираются из соответствующих таблиц контрольных работ согласно номеру зачетной книжки и первыми шестью буквами русского алфавита, которые необходимо расположить под номером, например:

номер – 2 8 7 0 5 2

буквы – а б в г д е

Если номер зачетной книжки состоит из четырех или пяти цифр, первые цифры шестизначного шифра принимаются равными нулю.

Из каждого вертикального столбца таблицы, обозначенного внизу определенной буквой, надо взять только одно число, стоящее в той горизонтальной строке, номер которой совпадает с номером буквы. Например, вертикальные столбцы таблицы 2 исходных данных к задаче 2 обозначены буквами «е», «г» и «д». В этом случае при указанном выше личном номере 287052 необходимо взять из столбца «е» вторую строку (второй тип сечения), из столбца «г» – нулевую строку (швеллер 36) и из столбца «д» – пятую строку (равнобокий уголок 90×90×6).

Работы, выполненные с нарушением этих указаний, не зачитываются.

К выполнению контрольных заданий следует приступать только после изучения соответствующего раздела курса.

В заголовке контрольной работы должны быть четко написаны: номер контрольной работы, название дисциплины, фамилия, имя и отчество (полностью), шифр группы.

Каждую контрольную работу следует выполнять в тетради стандартного формата четким почерком или компьютерным набором с полями 5 см для замечаний рецензента.

Перед решением задачи надо написать полностью ее условие с числовыми данными, составить аккуратный эскиз в масштабе и указать в нем в числах все величины, необходимые для расчета.

Решение должно сопровождаться краткими, последовательными и грамотными, без сокращения слов, объяснениями и чертежами, на которых все входящие в расчет величины должны быть показаны в числах. Необходимо указывать размерность всех величин.

После проверки контрольной работы преподавателем при наличии ошибок она возвращается студенту. При этом студент должен исправить в ней все сделанные ему указания. Исправления выполняются на отдельных листах, вкладываемых в соответствующие места рецензированной работы.

Контрольные работы

Задача 1 – Расчет статически неопределимых стержневых систем

Задание. Абсолютно жесткий брус опирается на шарнирно-неподвижную опору и прикреплен к двум стержням с помощью шарниров (рисунок 1).

Рисунок 1 – Схемы шарнирно-стержневых систем

Требуется:

1) найти усилия (N) в стержнях, выразив их через силу F;

2) найти допускаемую нагрузку F´_доп, приравняв большее из напряжений в двух стержнях к допускаемому напряжению [σ]=160 МПа;

3) найти предельную грузоподъемность системы и допускаемую нагрузку F´´_доп, если предел текучести σ_т=240 МПа и запас прочности k = 1,5;

4) сравнить величины F_доп, полученные при расчете по допускаемым напряжениям (см. п. 2) и допускаемым нагрузкам (см. п. 3). Данные взять из таблицы 1.

Таблица 1 – Исходные данные к задаче 1

Схема по рисунку 1	A, см2	a	b	c
	м
		2,1 2,2 2.3 2,4 2,5 2,6 2,7 2,8 2,9 3,0	2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0	1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0
е	в	г	д	е

Для определения двух неизвестных усилий в стержнях следует составить одно уравнение статики и одно уравнение совместности деформаций. При этом направления усилий в отброшенных стержнях выбирать по правилу: если стержень получает удлинение, то усилие в нем направлять от узла крепления, и, наоборот, если стержень укорачивается, то к узлу.

Для ответа на третий вопрос задачи следует иметь в виду, что в одном из стержней напряжение больше, чем в другом; условно назовем этот стержень первым. При увеличении нагрузки напряжение в первом стержне достигнет предела текучести раньше, чем во втором.

Когда это произойдет, напряжение в первом стержне не будет некоторое время расти даже при увеличении нагрузки и будет оставаться равным σ_т. Отсюда усилие в первом стержне:

N₁ = σ_тF₁. (1)

При дальнейшем увеличении нагрузки напряжение и во втором стержне достигнет предела текучести:

N₂ = σ_тF₂. (2)

Написав уравнение статики и подставив в него значения усилий (1) и (2), найдем из этого уравнения предельную грузоподъемность .

Пример 1. Рассмотрим шарнирно – стержневую систему, представленную на рисунке 2.

Рисунок 2 – Схема шарнирно – стержневой системы

Данные для расчета:

а = 4 м; в = 3 м; с = 2 м; A = 10 м²; α = 45˚; = 160 МПа;

= 240 МПа.

Примечание – брус ВАС считать абсолютно жестким.

Решение

1. Найдем усилия и напряжения в стержнях.

Для определения напряжений от действия внешней нагрузки в деформируемых стержнях 1 и 2 необходимо знать внутренние усилия в этих стержнях N и N , которые направлены вдоль стержней (рисунок 3). От действия заданной нагрузки F в неподвижном шарнире А возникают реактивные силы V и Н . Для определения усилий в стержнях рассмотрим условия статического равновесия данной системы.

Рисунок 3 – Схема к определению усилий в стержнях

Статическая сторона задачи

Приведем уравнения статического равновесия стержня ВАС. Поскольку система плоская, составим три уравнения:

; Н N cos = 0; (1)

; V + N – N sin F = 0; (2)

; N в + N a sin – F(c+в) = 0. (3)

В этих трех уравнениях имеется четыре неизвестных усилия. Поскольку величины опорных реакций V и Н по условию задачи определять не требуется, то для дальнейшего решения задачи пользуемся уравнением (3). В этом уравнении два неизвестных, таким образом, задача один раз статически неопределима. Дополнительное уравнение составляем из условия совместности перемещений, т.е. геометрической зависимости между деформациями стержней.

Геометрическая сторона задачи

Под действием силы F брус ВАС повернется и займет положение В АС (рисунок 3), при этом точка С перейдет в положение С , а точка В – в положение В , перемещаясь по нормали к первоначальному положению бруса ВАС вследствие малости угла поворота. Тогда отрезок СС является удлинением стержня 1. Чтобы найти величину удлинения стержня 2, необходимо на направление стержня 2 из точки В опустить перпендикуляр. Отрезок В₁D представляет собой удлинение стержня 2. Таким образом,

СС = ∆ , В₁D = ∆ .

Установим зависимость между величинами ∆ и ∆ . Из подобия треугольников АВВ и АСС можно записать:

,

где (из ∆ BB D).

Тогда

, или .

Следовательно,

. (4)

Уравнение (4) представляет зависимость между удлинениями стержней системы.

Физическая сторона задачи

Удлинения стержней 1 и 2 выражаем через усилия N и N по закону Гука:

; .

Тогда выражение (4) запишем так:

в.

Зная, что в и ,

получаем

и затем

2 . (5)

Решив совместно уравнение (3) и (5), выразим усилия N и через F:

Из второго уравнения выразим N :

Подставим это выражение в первое уравнение системы

.

Выполним преобразования

F.

Тогда

F.

Определим напряжения в стержнях в долях F:

F;

F.

2. Определим допускаемую нагрузку F´_доп из расчета по допускаемым напряжениям, приравняв максимальное напряжение в стержне к допускаемому :

740F´ =1.6 Н/м .

Отсюда

F´ кН.

3. Определим предельную грузоподъемность системы и допускаемую нагрузку F´´_доп из расчета по предельному состоянию.

Несущая способность системы будет исчерпана тогда, когда в обоих деформируемых стержнях напряжение достигнет предела текучести.

Предельные внутренние усилия в стержнях 1 и 2 при этом равны:

кН,

= кН.

Предельную грузоподъемность определим из условия статического равновесия (3):

N .

Отсюда

F = кН.

Допускаемая нагрузка при запасе прочности k = 1,5:

F´´_доп кН.

4. Сравним величины F из расчета по допускаемым напряжениям и допускаемым нагрузкам. Сопоставление показывает, что F´´_доп превышает F´_доп на

.

Задача 2 – Геометрические характеристики плоских сечений

Задание. Для заданного в таблице 2 поперечного сечения, состоящего из швеллера и равнополочного уголка, или из двутавра и равнополочного уголка, или швеллера и двутавра (рисунок 4), требуется:

1) определить положение центра тяжести;

2) найти осевые и центробежный моменты инерции относительно осей (Z_c и Y_c), проходящих через центр тяжести сечения;

3) определить направление главных центральных осей (V и U);

4) найти моменты инерции относительно главных центральных осей;

5) вычертить сечение в масштабе 1:2 и указать на нем все оси и размеры в числах.

Таблица 2 – Исходные данные к задаче 2

Вид сечения по рисунку 4	Швеллер	Равнополочный уголок	Двутавр
		80 × 80 ×8
		80 × 80 × 6
		90 × 90 × 8
		90 × 90 × 7
		90 × 90 × 6	20a
		100 × 100 × 8
		100 × 100 × 10	22a
		100 × 100 × 12
		125 × 125 × 10	24a
		125 × 125 × 12
е	г	д	е

Рисунок 4 – Вид сечений

При расчете все необходимые геометрические и другие данные профилей следует брать из таблиц сортамента прокатной стали [2, 3, 4, 5, 6, 7].

В сечении, состоящем из двух фигур, центр тяжести всего сечения находится на отрезке, соединяющем центры тяжести этих фигур (ближе к большей).

Две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции сечения. Осевые моменты инерции относительно таких осей имеют экстремальные значения – один J_max, другой J_min и называются главными моментами инерции.

Если есть хотя бы одна ось симметрии фигуры, то эта ось и перпендикулярная к ней центральная ось являются главными центральными и, соответственно, центробежный момент инерции такой фигуры равен нулю.

Центробежные моменты инерции уголков приведены в соответствующих стандартах [6, 7]. Их значения являются положительными в том случае, если зев уголка с его центром тяжести располагается во втором или четвертом квадранте координатных осей, проведенных по боковым граням уголка. Отрицательное значение центробежный момент инерции принимает в первом и третьем квадрантах.

Пример 2. Для поперечного сечения, состоящего из швеллера и равнополочного уголка (рисунок 5) рассмотрим поставленные выше вопросы.

Рисунок 5 – Поперечное сечение

Примечание – при расчете все необходимые данные следует брать из таблиц сортамента стального проката, разбивая сложное сечение на прокатные профили (ни в коем случае не заменять части профилей прямоугольниками).

Данные для расчета:

Фигура 1 – швеллер № 20 ГОСТ 8240-97 (рисунок 6):

h мм; А см ;

в мм; z см;

J см⁴; J см .

Фигура 2 – уголок 80 80 8 ГОСТ 8509–93

в мм; А см ;

z см; J J ;

J см .

Рисунок 6 – Геометрические размеры сечений

Решение

1. Определим положение центра тяжести сложного сечения (рисунок 5). Разобьем сложное сечение на составляющие фигуры 1 и 2. За вспомогательные оси сечения выберем систему координат Z Y₂. Это удобно, так как в системе этих осей координаты центров тяжести элементарных фигур не будут принимать отрицательных значений. Найдем координаты центра тяжести сложного сечения по формулам:

; y ,

где , – суммарные статические моменты инерции эле-

ментарных фигур относительно вспомогатель-

ных осей Z Y₂.

z cм;

см;

В этом случае согласно рисунка 5:

z см; z =0;

= 0; у cм.

Полученные координаты центра тяжести сечения отложим от вспомогательных осей Z₁ Y₂ и через найденную точку проведем центральные оси Z_с Y_с параллельно осям Z Y .

2. Найдем величины осевых и центробежных моментов инерции сечения относительно центральных осей Z_с Y_с. Для этого используем формулы перехода от центральных осей к параллельным:

;

;

, (1)

где , осевые и центробежные моменты

инерции элементарных фигур от-

носительно центральных осей

всей сложной фигуры;

, – осевые моменты инерции этих же фигур относи-

тельно собственных центральных осей. Эти ве-

личины найдены по таблицам сортамента прокат-

ных профилей;

координаты центров тяжести швеллера и уголка от-

носительно центральных осей всего сечения;

– центробежные моменты инерции швеллера и уголка

относительно собственных центральных осей.

Как видно из рисунка 5,

см;

см;

см;

см.

Поскольку оси Z Y являются главными осями сечения швеллера, то .

Для определения знака уголка пользуемся правилом: если зев уголка с его центром тяжести располагается в 1 или 3 квадрантах координатных осей, центробежный момент инерции принимается отрицательным, если в 2 или 4 квадрантах – положительным. В нашем случае зев уголка расположен в 3 квадранте, значит

J см .

Подставив численные значения в формулы (1), получим:

2075 м⁴;

см⁴;

= – 313,3 см⁴.

3. Определим направление главных центральных осей V и U. Угол наклона главных центральных осей V и U к осям Z_c и Y_с найдем по формуле:

Тогда 2 = 20,4˚; =10,2˚.

Поворачивая оси Ζ_с и Y_с против часовой стрелки (при положительном значении угла α) на угол α = 10,2˚, получаем положение главных центральных осей (рисунок 5).

4. Найдем величины моментов инерции относительно главных центральных осей по формуле:

.

Подставив числовые значения, получим:

Ось максимума (V) наклонена под меньшим углом к той из центральных осей, относительно которой центральный момент инерции сечения больше. В нашем случае

,

значит угол α получается между осями Z_c и V.

Выполним проверку по известному равенству

,

2130 .

Следовательно, задача решена верно.

Задача 3 – Плоский изгиб прямых брусьев

Задание. Для заданных двух схем балок (рисунки 7, 8) требуется написать выражения для поперечных сил Q и изгибающих моментов M для каждого участка в общем виде, построить эпюры Q и M, найти M_max и подобрать:

а) для схемы а – деревянную балку круглого поперечного сечения при [σ] = 8 МПа;

б) для схемы б – стальную балку двутаврового поперечного сечения при [σ] = 160 МПа. Данные взять из таблицы 3.

Чтобы построить эпюры (графики) Q и М, надо помнить, что поперечная сила в любом сечении есть алгебраическая сумма проекций всех внешних сил, действующих по одну сторону сечения, на ось, перпендикулярную оси балки. Поперечная сила Q считается положительной, если внешняя сила слева от сечения направлена снизу вверх, а справа – сверху вниз, и отрицательна – в противоположном случае.

Изгибающий момент в любом сечении определяется как алгебраическая сумма моментов всех внешних сил, действующих по одну сторону от этого сечения. Изгибающий момент считается положительным от тех нагрузок, момент которых изгибает горизонтальную балку выпуклостью вниз. Для построения эпюр Q и М необходимо разбить балку на грузовые участки; граница участка – это место приложения сосредоточенной внешней нагрузки или начало (конец) распределенной нагрузки.

Эпюра изгибающих моментов изображается на растянутых волокнах балки (в сторону ее выпуклости), а так как положительный момент соответствует направлению выпуклостью вниз, то положительный момент откладывается вниз, а отрицательный – вверх.

Для проверки правильности построения эпюр необходимо помнить, что в сечении, в котором к балке приложена сосредоточенная внешняя сила, перпендикулярная оси балки (в том числе и опорная реакция в виде сосредоточенной силы), значение поперечной силы Q изменяется скачкообразно на величину приложенной силы. Аналогично, в сечении, в котором к балке приложен сосредоточенный изгибающий момент (в том числе и опорная реакция в виде сосредоточенного момента), значение изгибающего момента М изменяется скачкообразно на величину приложенного момента.

Изгибающий момент достигает максимума или минимума в сечениях балки, в которых поперечная сила равна нулю.

Рисунок 7 – Расчетные схемы балок

Рисунок 8 – Расчетные схемы балок (продолжение)

Таблица 3 – Исходные данные к задаче 3

Схема по рисункам 7, 8	l1	l2	Расстояние в долях пролета	М, кН×м	F, кН	q, кН/м
	м	a1/a	а2/а	а3/а
	1,1
	1,2
	1,3
	1,4
	1,5
	1,6
	1,7
	1,8
	1,9
	2,0
е	д	е	г	д	е	г	д	е

Пример 3. Рассмотрим две схемы балок, представленных на рисунке 9.

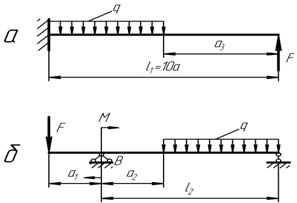
Рисунок 9 – Схемы балок

Данные для расчета:

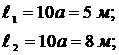
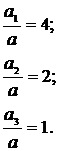F = 20 кН; q = 20 кН/м; М = 40 кНм;

Для схемы (а): Для схемы (б):

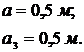
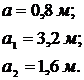
Решение

Схема (а), рисунок 10

1. Для балки, защемленной одним концом (консольная балка), удобно отсчитывать участки от свободного конца. В этом случае расчет можно вести без определения опорных реакций.

Составим уравнения поперечных сил Q и изгибающих моментов М для участков.

Участок 1: 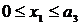; Q₁ = – F = – 20 кН, М₁ = Fx;

при x₁ = 0 М₁ = 0, при х₁ = 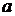₃ = 0,5 м М₁ = 20 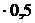= 10 кНм.

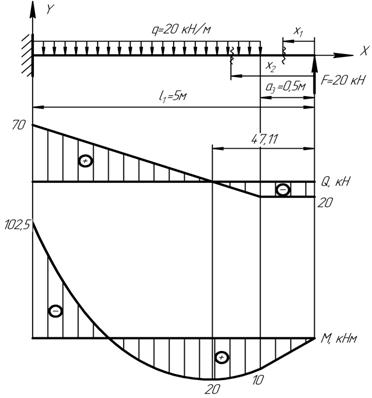
Рисунок 10 – К расчету балки

Участок 2: ;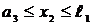

Q₂ = – F + q (x₂ – 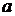₃), М₂ = Fx₂ – q ;

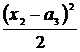при x₂ = 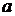₃ = 0,5 м Q₂ = – F = – 20 кН, М₂ = 20 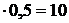кНм;

при x₃ = 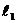= 5 м Q₂ = – 20 + 20(5 – 0,5) = 70 кН,

М₂ = 20 .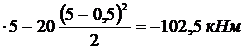

На этом участке Q меняет знак. Найдем значение x₂ = x₀, при котором Q = 0.

Q₂ = – F + q (x₂ – a₃) = 0; x₂ = x₀ = 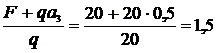м.

В этом сечении балки момент экстремален.

При x₂ = 1,5 м М_max = 20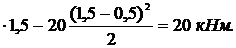

Отложим положительные ординаты Q вверх, а отрицательные – вниз и, соединив полученные точки линиями, получим эпюру поперечных сил (рисунок 10). Эпюра изгибающих моментов строится на растянутых волокнах балки, т.е. положительные значения М откладываются ниже нулевой линии, отрицательные – выше.

2. Подбор размеров поперечного сечения балки. Условие прочности при изгибе запишем:

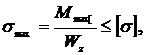
где W_z= 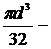осевой момент сопротивления поперечного сечения;

М_max = 102,5 кНм – максимальный изгибающий момент.

Тогда условие прочности можно представить в виде:

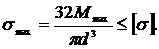
Отсюда определим диаметр поперечного сечения балки:

.

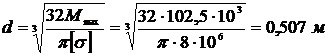Схема (б), рисунок 11

1. Для построения эпюр Q и М необходимо определить опорные реакции из уравнений статики:

.

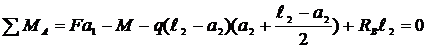Отсюда

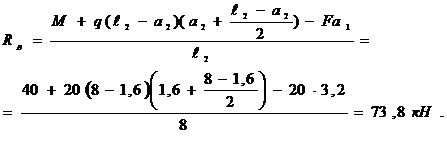
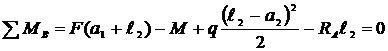
и отсюда же

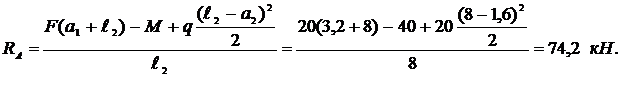
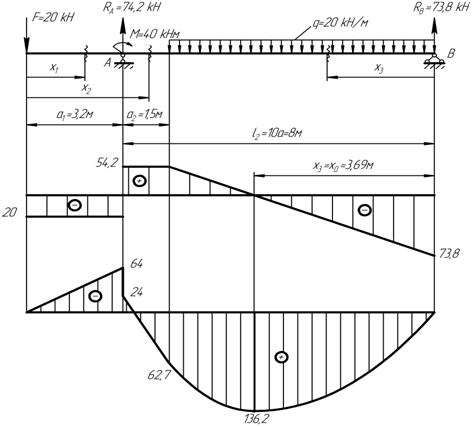
Рисунок 11 – Расчетная схема балки и эпюры Q и M

Выполним проверку:

.

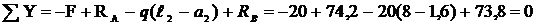Следовательно, реакции определены верно.

2. Составим выражения для определения поперечной силы и изгибающего момента.

Участок 1: 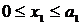; Q₁ = – F= – 20 кН, М₁ = – Fх₁;

при х₁ = 0 М₁ = 0; при х₁ = 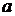₁ = 3,2м М₁ = – 20 .

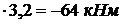Участок 2: 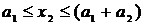; Q₂ = – F+R_A = – 20 + 74,2 = 54,2 кН,

М₂ = – F 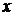₂ + М + R_A(x₂ – 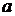₁);

при х₂ = 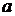₁ = 3,2 м М₂ = – 20 ;

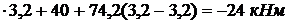при х₂ = 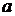₁ + 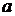₂ = 4,8 м М₂ = – 20 .

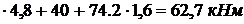Участок 3: ; ;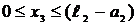

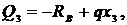
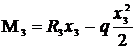при х₃ = 0 Q₃ = – R_B = – 73,8 кН, М₃=0;

при х₃ = 6,4 м Q₃ = – 73,8+20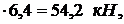

М₃ = 73,8 .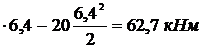

Определим экстремальное значение момента, так как поперечная сила на третьем участке изменяет знак:

Q₃ = – R_B + qx₃ = 0, х₃ = х₀ = ;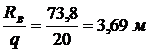

М_max = 73,8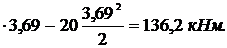

По полученным данным построим эпюры изгибающих моментов и поперечных сил.

3. Подберем размеры поперечного сечения двутавровой балки.

Для опасного сечения с М_max = 136,2 кНм из условия прочности при изгибе

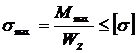
получим W_Z =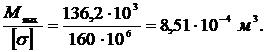

Из таблицы сортамента прокатных профилей (ГОСТ 8339–89) подберем двутавр с ближайшим большим значением W_Z : № 40, W_Z = 9,47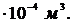

Задача 4 – Статически определимая рама

Задание. Для одной из рам, изображенной на рисунке 12, требуется:

1) написать выражения для продольных сил N, поперечных сил Q и изгибающих моментов M на каждом участке в общем виде;

2) построить эпюры N, Q и M;

3) подобрать двутавровое сечение при ;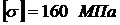

4) определить горизонтальное перемещение точки 1 и угловое перемещение сечения в точке 2.

Данные взять из таблицы 4.

Для ломаных стержней и рам ординаты эпюры M, как и в балках, откладываются со стороны растянутого волокна.

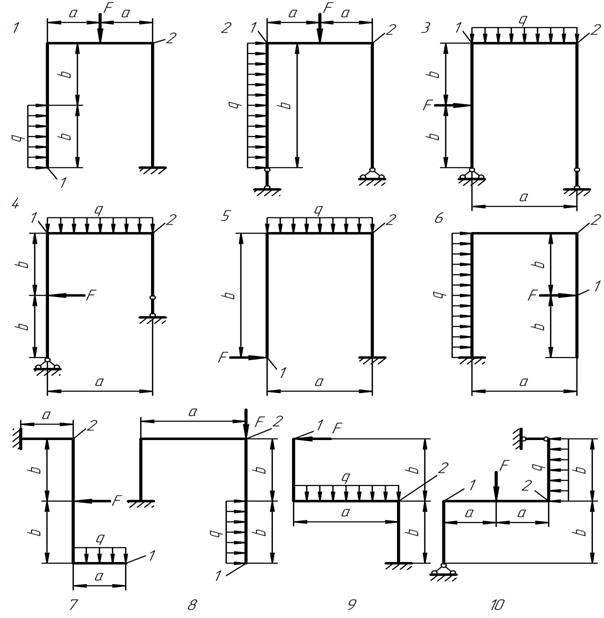
Рисунок 12 – Схемы рам

Таблица 4 – Исходные данные к задаче 4

№ схемы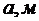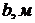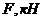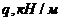
	3,0 2,9 2,8 2,7 2,6 2,5 2,4 2,3 2,2 2,1	3,0 2,9 2,8 2,7 2,6 2,5 2,4 2,3 2,2 2,1
e	д	е	д	е

Пример 5. Рассмотрим раму, представленную на рисунке 13.

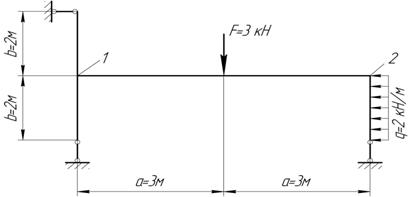
Рисунок 13 – Заданная схема рамы

Решение

1. Определим опорные реакци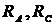и и 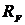(рисунок 14).

Определим опорные реакци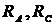и и 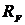(рисунок 14).

Для этого составим три уравнения равновесия:

, ,

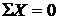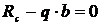откуда ;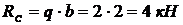

, ,

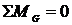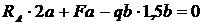откуда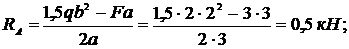

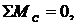
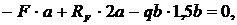
откуда

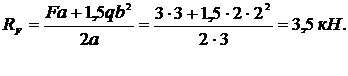
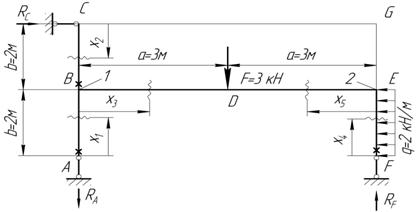
Рисунок 14 – Расчетная схема рамы

Проверка реакций опор:

, ;

, ; .

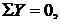
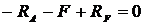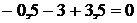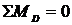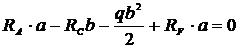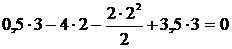Опорные реакции найдены верно.

Составим выражения N, Q и M для всех участков рамы, строго соблюдая правила определения знаков внутренних усилий.

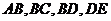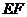Раму можно представить из пяти участков: и (рисунок 14).

Для всех участков ось X направляется вдоль стержней, т.е. мысленно представляем вертикальные участки рамы как горизонтальные. При этом нижние концы этих элементов (на рисунке 14 отмечены крестиком) принимаем в качестве левых концов участков.

На каждом участке проведем по одному сечению, определяемому координатой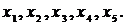

Участок : .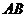

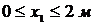Алгебраическая сумма проекций односторонних сил на ось стержня дает усилие

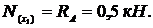
Алгебраическая сумма проекций односторонних сил на само сечение стержня дает усилие

.

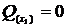Алгебраическая сумма моментов односторонних сил относительно центра тяжести сечения дает изгибающий момент

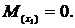
Участок : ;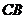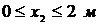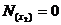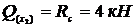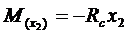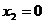

; ; ;

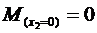при , при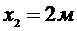

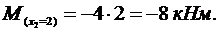
Участок 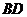: