Рассмотрим выборку с повторениями

Элементы комбинаторики

Комбинаторика – это наука о расположении элементов в определенном порядке и о подсчете числа способов такого расположения.

Комбинаторный принцип умножения если одну часть действия можно выполнить 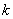способами, а другую - 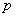способами, то все действие можно выполнить 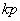числом способов.

Пример. Пусть требуется составить набор из ручки, карандаша и линейки. Имеется:

5 различных ручек,

7 различных карандашей,

10 различных линеек.

Сколькими способами можно составить требуемый набор?

Решение. Действием в данном случае является составление набора из ручки, карандаша и линейки; действие распадается на три этапа (части): выбрать ручку, выбрать линейку и выбрать карандаш. Первую часть действия – выбрать ручку – можно выполнить пятью способами, вторую часть действия – выбрать карандаш – можно выполнить семью способами, третью часть действия – выбрать линейку – можно выполнить десятью способами. Тогда все действие можно выполнить

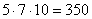
Число способов. Т.е. возможно 350 вариантов такого набора.

Пример.Сколько существуетнаборов длины из нулей и единиц?

Решение. Действием в данном случае является составление набора длины из нулей и единиц.

Набор будет составлен, если все позиций (мест) будут заполнены нулями и единицами. Действие распадается на частей: заполнить первую позицию, вторую и т.д., заполнить -ю позицию. Первую часть действия – написать первую компоненту - можно двумя способами: можно написать 0, а можно написать 1, написать вторую компоненту тоже можно двумя способами, и так все мест в наборе: на каждом месте можно написать либо 0 либо 1:

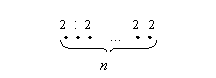
Тогда все действие согласно комбинаторному принципу умножения можно выполнить 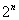числом способов:

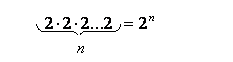
Комбинаторный принцип сложения. Если два действия взаимно исключают друг друга, и одно из них можно выполнить 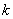способами, а другое - 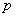способами, то оба действия можно выполнить 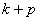числом способов.

Пример.

Выборкой объема 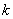из множества 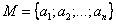называется всякая последовательность из 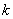элементов множества .

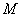Если элементы в выборке не повторяются, то выборка называется бесповторной, иначе – выборкой с повторениями

При бесповторной выборке все равно, каким образом осуществляется выбор: берутся все элементы сразу, или же поочередно (по одному).

Расположение элементов выборки в определенном порядке называется упорядочением , при этом выборка называется упорядоченной, в противном случае – неупорядоченной.

Рассмотрим бесповторную выборку

Расположение различных элементов в определенном порядке называется перестановкойбез повторений из элементов.

Например, на множестве из трех элементов 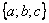возможны следующие перестановки: .

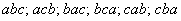Число различных перестановок без повторений из элементов обозначается 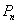и равно 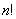, т.е.

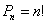
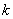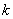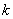Сочетанием без повторений из элементов по называется неупорядоченное -элементное подмножество -элементного множества. Число сочетаний без повторений из элементов по равно :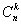

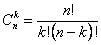
Например, требуется подсчитать, сколькими способами можно составить бригаду из трех человек для дежурства в группе из 30 человек. Поскольку порядок расположения людей в бригаде не фиксируется и люди не повторяются, то мы имеем случай сочетаний из 30 элементов по 3 без повторений:

.

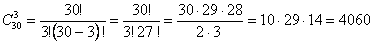Таким образом, бригаду дежурных из трех человек в группе из 30 человек можно выбрать 4060 различными способами.

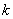Размещением без повторений из элементов по называется упорядоченное 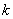-элементное подмножество -элементного множества.

Теорема.

Число размещений без повторений из элементов по 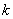равно:

.

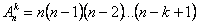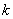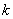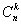Доказательство. Чтобы получить упорядоченное -элементное подмножество -элементного множества, нужно выполнить два этапа: выбрать элементов из (это можно выполнить числом способов) и затем упорядочить выбранные элементы (это можно сделать 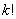числом способов). Согласно комбинаторному принципу умножения, все действие - получить упорядоченное 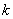-элементное подмножество -элементного множества – можно 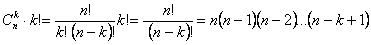числом способов.

Свойства сочетаний без повторений:

1)

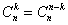
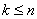
Доказательство. Поскольку 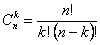и 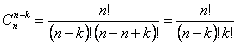, то утверждаемое очевидно.

2) 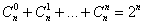(без доказательства).

Значения 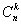могут быть найдены не расчетом по формуле количества сочетаний, а с помощью так называемого треугольника Паскаля. (Блез Паскаль (1623 – 1662) – французский математик).

Этот треугольник имеет вид:

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

1 7 21 35 35 21 7 1

1 8 28 56 70 56 28 8 1

Закономерность его построения такова: складывая две рядом стоящие числа, получаем число, стоящее ниже между ними. Первая строчка – значения числа сочетаний из 1 ( 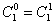), вторая – из 2 ( 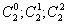- слева направо), и т.д.

Примеры.

1) Вероятность выпадения 5 очков на грани кубика равна 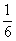, поскольку кубик может упасть любой из 6 граней кверху, а 5 очков находятся только на одной грани.

2) Вероятность выпадения герба при однократном бросании монеты - 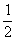, поскольку монета может упасть гербом или решкой – два исхода опыта, а герб изображен лишь на одной стороне монеты.

3) Если в урне 12 шаров, из которых 5 – черные, то вероятность вынуть черный шар - 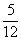, поскольку всего исходов опята – 12, а благоприятных из них - 5

Замечание. Классическое определение вероятности применимо при двух условиях:

1) все исходы опыта должны быть равновероятными;

2) опыт должен иметь конечное число исходов.

На практике бывает сложно доказать, что события равновероятные: например, при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д., кроме того, существуют опыты с бесконечным числом исходов.

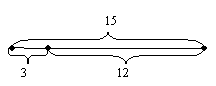
Пример. Ребенок бросает мяч, и максимальное расстояние, на которое он может забросить мяч – 15 метров. Найти вероятность того, что мяч улетит за отметку 3 м.

Решение. Искомую вероятность предлагается считать, как отношение длины отрезка, находящегося за отметкой 3 м (благоприятная область) к длине всего отрезка (всевозможные исходы):

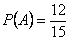
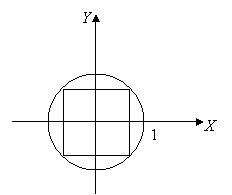
Пример. Точку случайным образом бросают в круг радиуса 1. Какова вероятность того, что точка попадет во вписанный в круг квадрат?

Решение. Под вероятностью того, что точка попадет в квадрат, понимают в данном случае отношение площади квадрата (благоприятной площади) к площади круга (общая площадь фигуры, куда бросают точку):

Диагональ квадрата равна 2 и выражается через его сторону по теореме Пифагора:

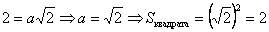
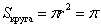
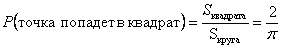
Аналогичные рассуждения проводят и в пространстве: если в теле объема случайным образом выбирается точка, то вероятность того, что точка окажется в части тела объема 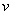, вычисляется как отношение объема благоприятной части к общему объему тела:

.

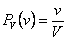Объединяя все случаи, можно сформулировать правило вычисления геометрической вероятности:

Если в некоторой области 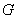случайным образом выбирается точка, то вероятность того, что точка окажется в части 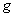этой области равна:

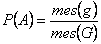, где

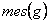- обозначает меру области: в случае отрезка – это длина, в случае плоской области – это площадь, в случае пространственного тела – это объем, на поверхности – площадь поверхности, на кривой – длина кривой.

Интересным приложением понятия геометрической вероятности является задача о встрече.

Задача. (О встрече)

Два студента договорились о встрече, например, в10 часов утра на следующих условиях: каждый приходит в любое время в течение часа с 10 до 11 и ждет 10 минут, после чего уходит. Какова вероятность встречи?

Решение. Проиллюстрируем условия задачи следующим образом: на оси 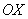отложим время, идущее для первого из встречающихся, а на оси - время, идущее для второго. Поскольку эксперимент длится один час, то по обеим осям отложим отрезки длины 1. Моменты времени, когда встречающиеся пришли одновременно, интерпретируется диагональю квадрата.

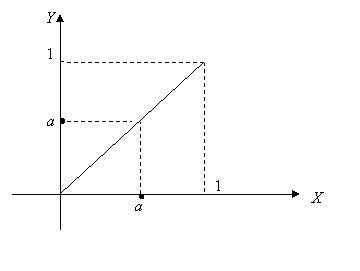
Пусть первый пришел в некоторый момент времени 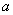. Студенты встретятся, если время прибытия второго на место встречи заключается в промежутке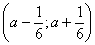

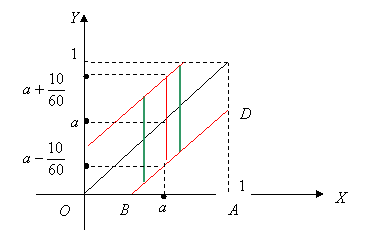
Рассуждая так для любого момента времени , получим, что область времени, интерпретирующая возможность встречи («пересечение времён» нахождения на нужном месте первого и второго студентов) находится между двумя прямыми: и . Вероятность встречи определяется по формуле геометрической вероятности:

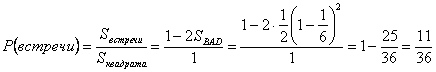
В 1933 г. Колмогоров А.М. (1903 - 1987) предложил аксиоматический подход к построению и изложению теории вероятности, который стал общепринятым в настоящее время. При построении теории вероятности как формальной аксиоматической теории требуется не только ввести базовое понятие – вероятность случайного события, но и описать его свойства с помощью аксиом (утверждений интуитивно верных, принимаемых без доказательства).

Такими утверждениями являются утверждения, аналогичные свойствам относительной частоты появления события.

Относительной частотой появления случайного события 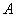называется отношение числа появлений события в испытаниях к общему числу проведенных испытаний:

.

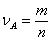Очевидно, 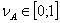, для достоверного события 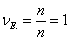, для невозможного события 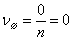, для несовместных событи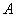й и 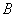верно следующее:

.

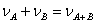Пример. Проиллюстрируем последнее утверждение. Пусть из колоды в 36 карт вынимают карты. Пусть событие 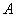означает появлениебубей, событие 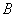означает появление червей, а событие 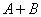- появление карты красной масти. Очевидно, события 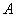и 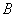несовместны. При появлении красной масти ставим метку возле события 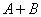, при появлении бубей – возле события 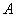, а при появлении червей – возле события 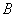. Очевидно, что метка возле события 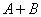будет поставлена тогда и только тогда, когда будет поставлена метка возле события 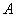или возле события 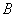, т.е. .

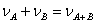Назовем вероятностью случайного события 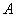число, сопоставленное событию 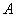по следующему правилу:

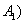
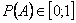
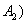
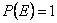
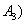
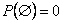
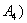Для несовместных событи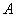й и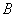

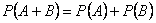
Итак,

Относительная частота	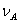Вероятность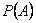
,	,

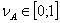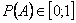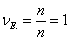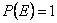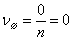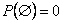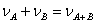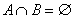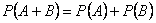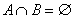При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это свойство называется свойством устойчивости относительной частоты. Число, около которого группируются относительные частоты появления события при проведении большой сери опытов, может быть принято за вероятность события. Такой способ определения вероятности события называется статистическим определением вероятности.

Например, Дж. Керрих, находясь в лагере во время второй мировой войны, провел 10 серий по 1000 опытов в каждой по бросанию монетки. Относительная частота выпадений герба была следующей:

,

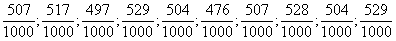что еще раз подтверждает, что вероятность выпадения герба при одном бросании монетки - .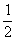

Кроме того, известно, что .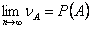

Таким образом, статистическое определение вероятности лучше всех других отражает сущность понятия вероятности случайного события, однако, отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта.

Теорема

Если события 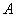и 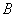независимы, то:

1) события 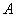и 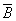независимы;

2) события 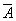и 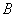независимы;

3) события 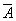и 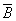независимы.

Доказательство. 1)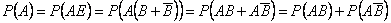

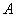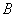Поскольку события и независимы, то:

.

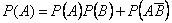Итак,

.

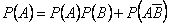
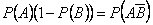Поскольку 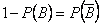, то 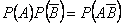, что свидетельствует о независимости событи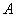й и .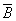

2)

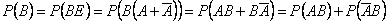
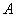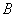Поскольку события и независимы, то:

.

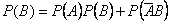Итак,

.

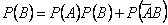
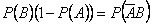Поскольку 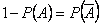, то 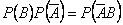, что свидетельствует о независимости событи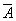й и .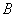

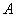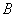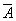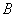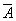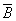3) Если события и независимы, то по 2) события и независимы; и по 1) и независимы.

Определение. События 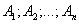независимыв совокупности, если

.

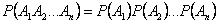Определение. События 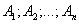попарно независимы, если в любой паре 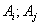события 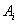и 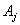независимы.

Независимость в совокупности и попарная независимость событий – понятия разные.

Пример. Три грани треугольной пирамиды окрашены соответственно в белый, зеленый, желтый цвета. На последней грани присутствуют все три цвета. Случайным образом выбирают грань. Найти вероятности событий: 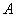=«на грани есть желтый цвет»;

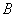=«на грани есть белый цвет»;

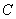=«на грани есть зеленый цвет»;

Решение. Желтый цвет имеется на двух гранях из четырех, т.о. 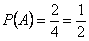; аналогично: 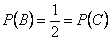. Вероятность того, что на выпавшей грани есть два цвета - 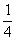, т.е. 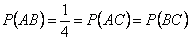. Таким образом,

,

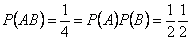
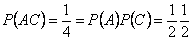
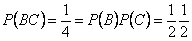Т.е. все события попарно независимы. Однако события не являются независимыми в совокупности:

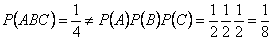
Теорема. (О появлении хотя бы одного из независимых событий)

Пусть вероятность появления каждого из п событий 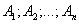, независимых в совокупности, равна 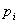. Вероятность появления хотя бы одного события, равна

,

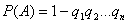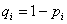
Доказательство. Поскольку по закону Де Моргана

,

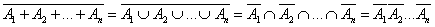то

.

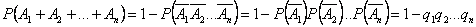Пример. Из полной колоды карт (52 шт.) одновременно вынимают четыре карты. Найти вероятность того, что среди этих четырех карт будет хотя бы одна бубновая карта.

Решение. Пусть событие 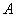означает «среди четырех вынутых карт есть хотя бы одна бубновая карта». Тогда 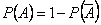. Событие 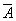означает, что все четыре карты не бубновой масти. Вероятность того, что случайно взятая из колоды карта не бубновая - и 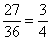, тогда ,

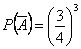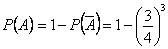
Пример. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Найти вероятность попадания в мишень при одном выстреле.

Если обозначить р – вероятность попадания стрелком в мишень при одном выстреле, то вероятность промаха при одном выстреле, очевидно, равна (1 – р).

Вероятность трех промахов из трех выстрелов равна (1 – р)³. Эта вероятность равна 1 – 0,875 = 0,125, т.е. в цель не попадают ни одного раза.

Получаем: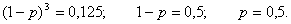

Пример. Чему равна вероятность того, что при бросании трех игральных костей 6 очков появится хотя бы на одной из костей?

Решение.

Вероятность выпадения 6 очков при одном броске кости (событие 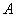) равна 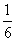. Вероятность того, что не выпадет 6 очков (событие 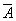) - 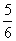. Вероятность того, что при броске трех костей не выпадет ни разу 6 очков равна .

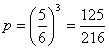Тогда вероятность того, что хотя бы один раз выпадет 6 очков, равна .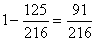

Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.

Вероятность того, что выстрелы производит первый, второй или третий стрелок равна .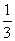

Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:

- для первого стрелка: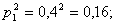

- для второго стрелка: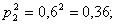

- для третьего стрелка: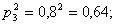

Искомая вероятность равна:

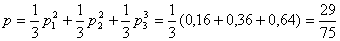
Пример. В барабане револьвера находятся 4 патрона из шести в произвольном порядке. Барабан раскручивают, после чего нажимают на спусковой крючок два раза. Найти вероятности следующих событий: первый выстрел, вторая осечка; первая осечка, второй выстрел, хотя бы одного выстрела, двух выстрелов, двух осечек.

Решение. Вероятность выстрела при первом нажатии на курок в условиях задачи - 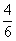. Вероятность того, что при втором нажатии на курок будет выстрел, если первым был выстрел, - 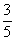, поскольку неизрасходованных патронов осталось 3, и гнезд, которые могут оказаться напротив бойка 5. Таким образом, вероятность двух последовательных выстрелов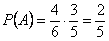

Вероятность осечки при первом нажатии на курок в условиях задачи равна 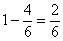. Вероятность того, что при втором нажатии на курок будет осечка, если первой была осечка, - 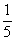, поскольку пустых гнезд осталось одно, и гнезд, которые могут оказаться напротив бойка 5. Таким образом, вероятность двух последовательных осечек .

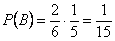Найдем вероятность события «осечка, выстрел». Вероятность осечки при первом нажатии на курок 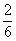, неиспользованных патронов остается - 4 , а всего возможных гнезд – 5, т.о. вероятность выстрела при втором нажатии на курок, если при первом нажатии на курок была осечка, - 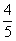. Тогда вероятность события «осечка, выстрел» - .

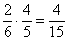Найдем вероятность события «выстрел, осечка». Вероятность выстрела при первом нажатии на курок 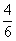, пустых гнезд остается - 2 , а всего гнезд – 5, т.о. вероятность осечки при втором нажатии на курок, если при первом нажатии на курок был выстрел, - 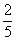. Тогда вероятность события «выстрел, осечка» - .

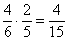Найдем вероятность хотя бы одного выстрела при двух нажатиях на курок (событие 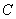) . Противоположным событием является событие «ни одного выстрела при двух нажатиях на курок», т.е. две осечки. Тогда равна

.

Найдем вероятность события «осечка, выстрел». Вероятность осечки при первом нажатии на курок 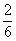, неиспользованных патронов остается - 4 , а всего возможных гнезд – 5, т.о. вероятность выстрела при втором нажатии на курок, если при первом нажатии на курок была осечка, - 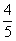. Тогда вероятность события «осечка, выстрел» - .

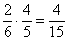Найдем вероятность события «выстрел, осечка». Вероятность выстрела при первом нажатии на курок 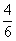, пустых гнезд остается - 2 , а всего гнезд – 5, т.о. вероятность осечки при втором нажатии на курок, если при первом нажатии на курок был выстрел, - 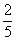. Тогда вероятность события «выстрел, осечка» - .

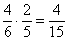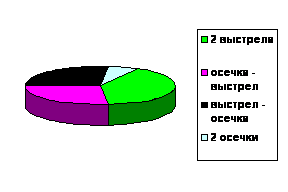
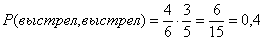- два выстрела подряд

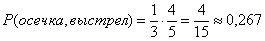- первая осечка, второй выстрел

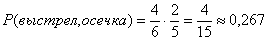- первый выстрел, вторая осечка

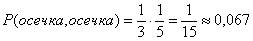- две осечки подряд

Эти четыре случая образуют полную группу событий (сумма их вероятностей равна единице)

Анализируя полученные результаты, видим, что вероятность хотя бы одного выстрела равна сумме 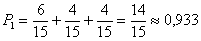или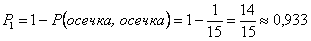

Теперь рассмотрим другой случай. Предположим, что после первого нажатия на курок барабан раскрутили и опять нажали на курок. Условные вероятности второго выстрела и осечки вычисляются из условия, что напротив бойка может оказаться то же гнездо, что и в первый раз.

Вероятности первого выстрела и первой осечки не изменились - ,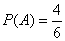

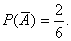
Условная вероятность выстрела при второй попытке - 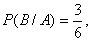если в первый раз был выстрел, 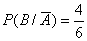- если в первый раз произошла осечка.

Условная вероятность осечки во второй раз - 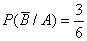, если в первый раз произошел выстрел, 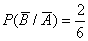- если была осечка.

Тогда:

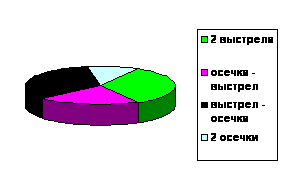
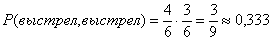- два выстрела подряд

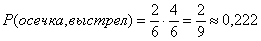- первая осечка, второй выстрел

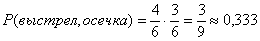- первый выстрел, вторая осечка

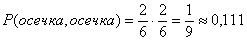- две осечки подряд

В этом случае вероятность того, что произойдет хотя бы один выстрел, равна

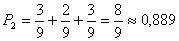или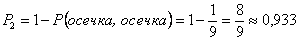

	после первого выстрела барабан не раскручивают	после первого выстрела барабан раскручивают

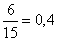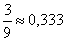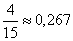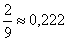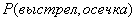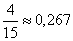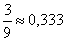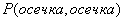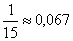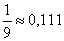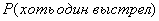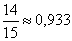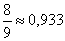Ниже показаны диаграммы вероятностей для первого и второго рассмотренных случаев.

Пример. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

Решение. Обозначим попадание в цель первым стрелком – событие А, вторым – событие В, промах первого стрелка – событие 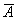, промах второго – событие .

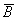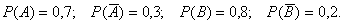
Вероятность того, что первый стрелок попадет в мишень, а второй – нет равна

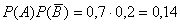
Вероятность того, что второй стрелок попадет в цель, а первый – нет равна

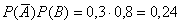
Тогда вероятность попадания в цель только одним стрелком равна

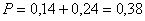
Тот же результат можно получить другим способом – находим вероятности того, что оба стрелка попали в цель и оба промахнулись. Эти вероятности соответственно равны:

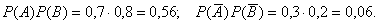
Тогда вероятность того, что в цель попадет только один стрелок равна:

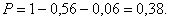
Пример. Вероятности того, что нужная деталь находится в первом, втором, третьем или четвертом ящике, соответственно равны 0,6, 0,7, 0,8, 0,9. Найти вероятности того, что эта деталь находится: а) не более, чем в трех ящиках; б) не менее, чем в двух ящиках.

Решение.

а) Вероятность того, что данная деталь находится во всех четырех ящиках, равна

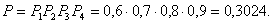
Вероятность того, что нужная деталь находиться не более, чем в трех ящиках равна вероятности того, что она не находится во всех четырех ящиках.

.

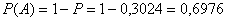б) Вероятность того, что нужная деталь находится не менее, чем в двух ящиках, складывается из вероятностей того, что деталь находиться только в двух ящиках, только в трех ящиках, только в четырех ящиках. Конечно, эти вероятности можно посчитать, а потом сложить, однако, проще поступить иначе. Та же вероятность ра