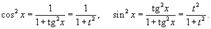Неопределенный интеграл: определение, свойства, табличные интегралы.

Определение первообразной и неопределенного интеграла.Функция F(x) называется первообразной функции f(x), если 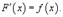Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как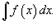

Таким образом, если F - некоторая частная первообразная, то справедливо выражение 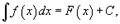где С - произвольная постоянная.

Свойства неопределенного интеграла. В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f,

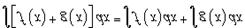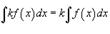а, k, C - постоянные величины.1) 2) 3)

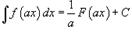
4)

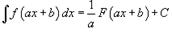
Таблица интегралов. В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).

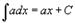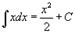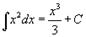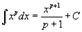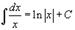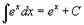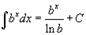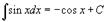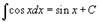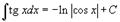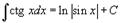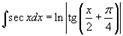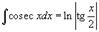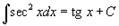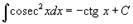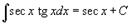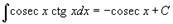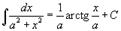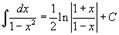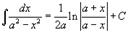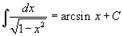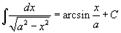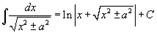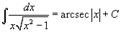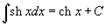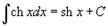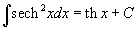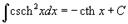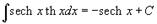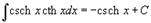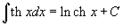Метод подстановки и метод интегрирования по частям.

Метод подстановки.Интегрирование путем введения новой переменной (метод подстановки) основано на формуле где х = ῳ(t) - дифференцируемая функция переменной t.

Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации.Формула интегрирования по частям следующая 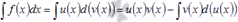.То есть, подынтегральное выражение f(x)dx представляем в виде произведения функции u(x) на d(v(x)) - дифференциал функции v(x). Далее находим функцию v(x) (чаще всего методом непосредственного интегрирования) и d(u(x)) - дифференциал функции u(x). Подставляем найденные выражения в формулу интегрирования по частям и исходный неопределенный интеграл сводится к разности 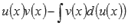. Последний неопределенный интеграл может быть взят с использованием любого метода интегрирования, в том числе и метода интегрирования по частям.

Интегрирование рациональных алгебраических и тригонометрических выражений.

Интегрирование любого рационального выражения тригонометрических функций можно всегда свести к интегрированию алгебраической рациональной функции используя универсальную тригонометрическую подстановку x = 2arctg t (или ). Для преобразования рациональных выражений от sin x, cos x, tg x, ctg x, sec x и cosec x в алгебраические рациональные функции переменной t применяются следующие тригонометрические формулы:

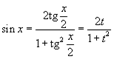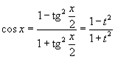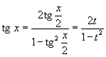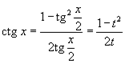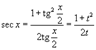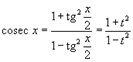Чтобы вычислить интеграл вида 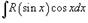, где R - рациональная функция, используется подстановка 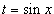. Аналогично, для вычисления интеграла вида 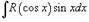, где R - рациональная функция, используется подстановка 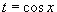. Если подынтегральное выражение является только функцией tg x, то подстановка t = tg x преобразует такой интеграл в интеграл от рациональной функции. Для вычисления интеграла вида 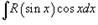, где обе функции sin x и cos x входят в четной степени, применяется подстановка t = tg x и формулы