Подсчитать определитель матрицы А.

Затем матрицей B заменить первый столбец матрицы А, подсчитать определитель и разделить его на detA, так мы получим x₁. То же самое проделать со 2-ым и 3-им столбцом.

Билет 12.

Решение произвольных систем. Теорема Кронекера-Капелли.

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Найти какой-либо базисный минор порядка r. Взять r уравнений, из которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор, называются главными и остаются слева, а остальные называются свободными и переносятся в правую часть уравнения. Найдя главные черезсвободные, получим общее решение системы.

Однородные система уравнений. Фундаментальная система решений.

Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю.

Билет 13. Бином Ньютона

Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона:

(a + b)ⁿ = aⁿ + C¹_n a^{n - 1} b + C²_n a^{n - 2} b² +...+C^k_n a^{n - k} b^k +... + C^{n - 1}_n ab^{n - 1} + Cⁿ_nbⁿ

или (после подстановки выражений C^k_n с учетом формулы C^k_n = C^{n - k}_n):

,

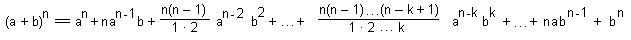где C^k_n — число всех возможных сочетаний, которые можно образовать из n элементов по k.

Пример:
(a + b)⁵ = a⁵ + C¹₅ a⁴b + C²₅ a³b² + C³₅ a²b³ + C⁴₅ ab⁴ + C⁵₅ b⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

Свойства бинома Ньютона

1. Разложение бинома (a + b)ⁿ представляет собой многочлен, расположенный по убывающим степеням a (от n-й до нулевой) и по возрастающим степеням b (от нулевой до n-й); сумма показателей a и b в каждом члене разложения равна показателю степени бинома. Число членов разложения на единицу больше показателя степени бинома.
2. Коэффициенты членов разложения («биноминальные коэффициенты») возрастают до середины разложения и затем убывают; коэффициенты каждой пары членов, равноотстоящих от начала и конца разложения, равны между собой. Если n четное, то имеется один средний наибольший коэффициент; если n нечетное, то имеется два средних наибольших коэффициента.
3. При возведении в n-ю степень разности a - b все четные члены разложения имеют знак "минус":

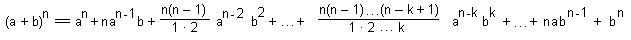
Билет 14. Функция, определение и способы задания. Обратная функция, суперпозиция функций.

Функция

ФУНКЦИЯ 1.Зависимая переменная величина.2.Соответствие y=f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение другой величины, y (зависимой переменной или Ф. в значении 1). Ф. задана, если известен закон, определяющий такое соответствие. На практике она задается формулой, таблицей или графиком. При построении графика функции анализируются такие ее свойства, как четность или нечетность, нулевые значения, периодичность, монотонность, наличие асимптоты и др. Важны еще два часто употребляемых понятия: функция, заданная в виде уравнения f(x,y) = 0, неразрешенного относительно y, называется неявной; функция, заданная в виде y= f(g(x)), т. е. функция функции, называется сложной Ф. или иначе — суперпозицией функций g и f. Сложную функцию часто записывают в виде y=f(u), где u=g(x), при этом u называют промежуточным аргументом. Множество X значений аргументов функции x ∈ X называетсяобластьюопределенияфункции, асоответственномножество Y = {y | y = f(x), x ∈ X} —областьюзначенийфункции, илиобластьюизмененияфункции.

Способы задания:

Аналитический :функция задается в виде одной или нескольких формул или уравнений.

Если область определения функции y=f(x) не указана , то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл. 1/1+х^2 ( -∞;∞)

Графический:задается график функции.

Табличный:функция задается таблицей ряда значений аргумента и соответствующих значений функции. Известные таблицы значений тригонометрических функций, логарифмические таблицы.

Обратная функция.Функция, обращающая зависимость, выражаемую данной функцией. Так, если у = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у, х = φ (y), является обратной по отношению к данной функции у = f (x).

Суперпозиция.Несколько функций , используются вместе.

Последовательность Xn называется возрастающей, если X1<X2<X3<…<Xn<…

Последовательность называется убывающей, если X1>X2>X3>…>Xn>…

Последовательность называется невозрастающей, если X1≥X2≥X3≥…≥Xn≥…

Все n последовательности называются монотонными.

Т.Пусть Xn монотонно возрастающая последовательность, если она ограничена сверху, то Xn<M, M = const

Если Xn монотонно убывающая последовательность, она имеет конечный предел, если она ограничена снизу Xn≥m, m=const