Каноническое уравнение эллипса.

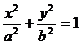
Теорема Лагранжа.

Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка e, a < e < b, такая, что .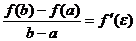

Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

Отношение 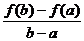равно угловому коэффициенту секущей АВ.

у

В

А

0 а e b x

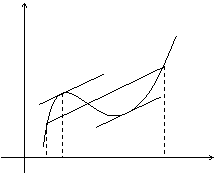
Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна секущей, соединяющей точки А и В. Таких точек может быть и несколько, но одна существует точно.

Доказательство. Рассмотрим некоторую вспомогательную функцию

F(x) = f(x) – y_{сек АВ}

Уравнение секущей АВ можно записать в виде:

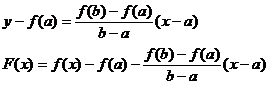
Функция F(x) удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b). По теореме Ролля существует хотя бы одна точка e, a < e < b, такая что F¢(e) = 0.

Т.к. 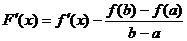, то 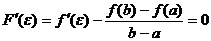, следовательно

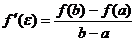
Теорема доказана.

3. Вычислить интеграл .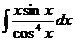

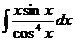
4. Вычислить .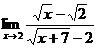

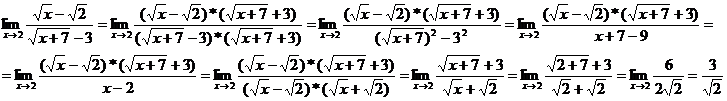
БИЛЕТ № 21.

Каноническое уравнение гиперболы.

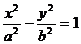
Производные параметрически и неявно заданных функций.

1. Производная функции, заданной параметрически.

Пусть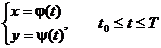

Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х). Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].

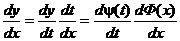
Т.к. Ф(х) – обратная функция, то 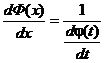. Окончательно получаем: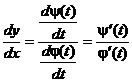

Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.

2. Производная неявно заданной функции.

Пусть дана дифференцируемая функция 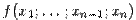, для которой в некоторой точке 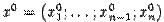выполнено неравенство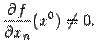

Тогда в некоторой окрестности точки 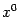уравнение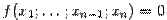

определяет, как мы знаем из теоремы о неявной функции, некоторую функцию 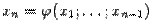, заданную вблизи точки 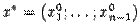в .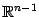

Пусть требуется найти её частные производные 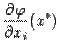, 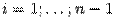. Это можно сделать, применив формулу производной сложной функции к функции

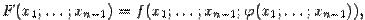которая тождественно равна 0 в окрестности точки 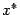; следовательно, и все её частные производные в точке 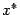обращаются в 0. Итак, считая параметром, от которого зависят все аргументы функции 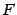, переменную 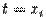, где 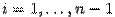, получаем по формуле :

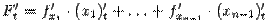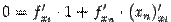
(производные 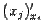равны 0 при 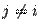, 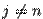), то есть 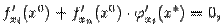откуда 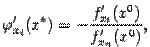или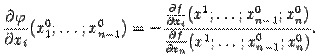

Эта важная формула позволяет вычислять производные неявно заданной функции 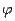, не имея задающего её явного выражения.

3. Выполнить действия .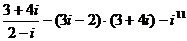

1.

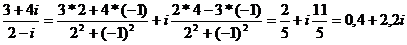
2.

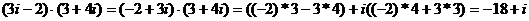
3.

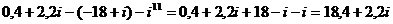
Найти точки разрыва, исследовать их характер и построить график функции

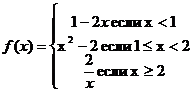
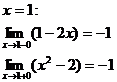
Устранимый разрыв.

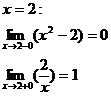
Разрыв 1-го рода.

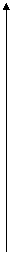у

0 1 2 х

-1

БИЛЕТ № 22.

1. Приведение уравнения кривой второго порядка к каноническому виду (без поворотов).

Кривая второго порядка может быть задана уравнением

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0.

1. Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

2. 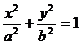- уравнение эллипса.

3. 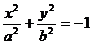- уравнение “мнимого” эллипса.

4. 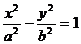- уравнение гиперболы.

5. a²x² – c²y² = 0 – уравнение двух пересекающихся прямых.

6. y² = 2px – уравнение параболы.

7. y² – a² = 0 – уравнение двух параллельных прямых.

8. y² + a² = 0 – уравнение двух “мнимых” параллельных прямых.

9. y² = 0 – пара совпадающих прямых.

10. (x – a)² + (y – b)² = R² – уравнение окружности.