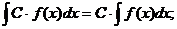Записать каноническое уравнение прямой, проходящей через точки А (2;-5) и В (4;7). Лежит ли точка С (0;17) на прямой АВ? Ответ обосновать.

Уравнение прямой, проходящей через 2 заданные точки – А и В:

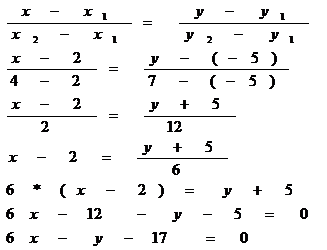
Проверка точка С:

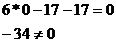
Точка С не лежит на прямой АВ.

4. Вычислить интеграл .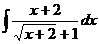

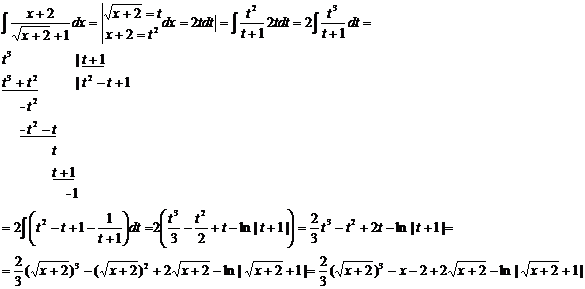
БИЛЕТ № 2.

Вычисление определителей второго, третьего и n-го порядка.

Определитель второго порядка:

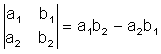
Определитель третьего порядка:

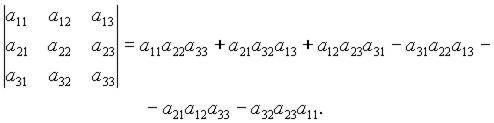
Определитель n-го порядка:

где M_1j — определитель квадратной матрицы, полученной из матрицы A вычеркиванием

первой строки и j-го столбца.

Вектор-функция. Интегрирование. Натуральный параметр.

Пусть каждому значению 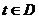поставлен в соответствие вектор 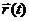трехмерного пространства. В этом случае говорят, что на множестве D задана векторная функция.

Если в пространстве задана декартова система координат, то задание вектор-функции 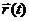означает задание скалярных функций x (t), y (t), z (t). Если 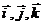– единичные векторы координатных осей, то .

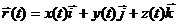Для вектор-функции 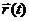, заданной на отрезке можно составить интегральные суммы и рассмотреть их предел при стремлении к нулю максимальной длины отрезков, на которые разбит отрезок [a;b]. Этот предел будет называться интегралом от 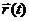по отрезку [a;b] и обозначаться 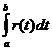. Этот предел существует только если 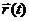непрерывна на отрезке [a;b]. На интегралы от вектор-функций распространяются обычные свойства интегралов от скалярных функций.

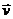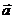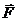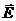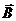Вектор-функции широко используются в физике. Так, скорость , ускорение , сила напряженности электрического и магнитного полей и плотность тока 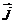являются векторными функциями координат.

Найти косинус угла при вершине С в треугольнике АВС, если известны координаты вершин треугольника: А (-1;0;4), В (0;-1;3) и С (1;0;4).

Угол АСВ – это угол между векторами и .

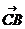(-1-1;0-0;4-4) = (-2;0;0)

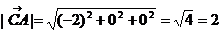
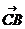(0-1;-1-0;3-4) = (-1;-1;-1)

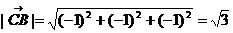
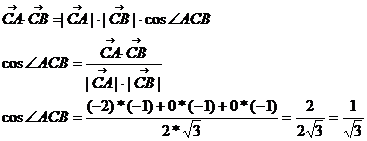
4. Вычислить интеграл .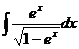

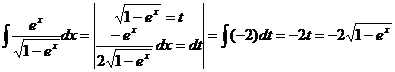
БИЛЕТ № 3.

Обратная матрица. Формула для нахождения обратной матрицы.

Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А^-1.

Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Общий подход к нахождению обратной матрицы.

Исходя из определения произведения матриц, можно записать:

AX = E Þ 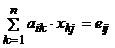, i=(1,n), j=(1,n),

e_ij = 0, i ¹ j,

e_ij = 1, i = j .

Таким образом, получаем систему уравнений:

,

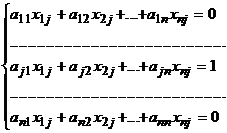Решив эту систему, находим элементы матрицы Х.

Но такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

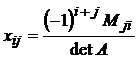
где М_ji – дополнительный минор элемента а_ji матрицы А.

Свойства неопределённого интеграла.

Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C.

Записывают: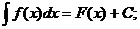

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

1.

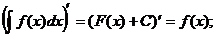
2.

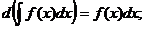
3.

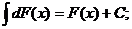
4. 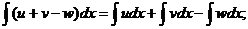где u, v, w – некоторые функции от х.

5.