Линейные операции над матрицами. Умножение матриц.
БИЛЕТ № 1.
Записать каноническое уравнение прямой, проходящей через точки А (2;-5) и В (4;7). Лежит ли точка С (0;17) на прямой АВ? Ответ обосновать.
Уравнение прямой, проходящей через 2 заданные точки – А и В:
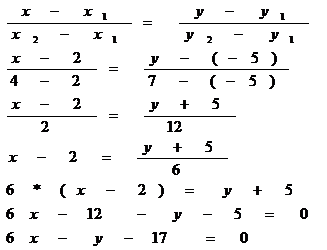
Проверка точка С:
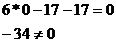
Точка С не лежит на прямой АВ.
4. Вычислить интеграл 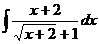 .
.
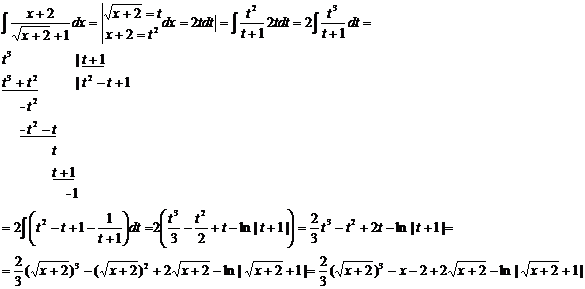
БИЛЕТ № 2.
Вычисление определителей второго, третьего и n-го порядка.
Определитель второго порядка:
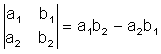
Определитель третьего порядка:
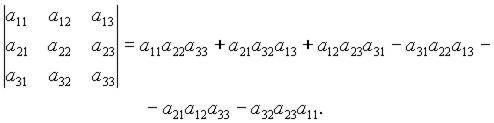
Определитель n-го порядка:

где M1j — определитель квадратной матрицы, полученной из матрицы A вычеркиванием
первой строки и j-го столбца.
Вектор-функция. Интегрирование. Натуральный параметр.
Пусть каждому значению 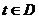 поставлен в соответствие вектор
поставлен в соответствие вектор 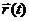 трехмерного пространства. В этом случае говорят, что на множестве D задана векторная функция.
трехмерного пространства. В этом случае говорят, что на множестве D задана векторная функция.
Если в пространстве задана декартова система координат, то задание вектор-функции 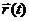 означает задание скалярных функций x (t), y (t), z (t). Если
означает задание скалярных функций x (t), y (t), z (t). Если 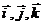 – единичные векторы координатных осей, то
– единичные векторы координатных осей, то 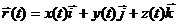 .
.
Для вектор-функции 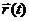 , заданной на отрезке можно составить интегральные суммы и рассмотреть их предел при стремлении к нулю максимальной длины отрезков, на которые разбит отрезок [a;b]. Этот предел будет называться интегралом от
, заданной на отрезке можно составить интегральные суммы и рассмотреть их предел при стремлении к нулю максимальной длины отрезков, на которые разбит отрезок [a;b]. Этот предел будет называться интегралом от 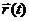 по отрезку [a;b] и обозначаться
по отрезку [a;b] и обозначаться 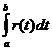 . Этот предел существует только если
. Этот предел существует только если 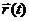 непрерывна на отрезке [a;b]. На интегралы от вектор-функций распространяются обычные свойства интегралов от скалярных функций.
непрерывна на отрезке [a;b]. На интегралы от вектор-функций распространяются обычные свойства интегралов от скалярных функций.
Вектор-функции широко используются в физике. Так, скорость 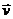 , ускорение
, ускорение 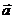 , сила
, сила 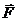 напряженности электрического и магнитного полей
напряженности электрического и магнитного полей 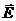 и
и 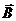 плотность тока
плотность тока 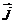 являются векторными функциями координат.
являются векторными функциями координат.
Найти косинус угла при вершине С в треугольнике АВС, если известны координаты вершин треугольника: А (-1;0;4), В (0;-1;3) и С (1;0;4).
Угол АСВ – это угол между векторами  и
и 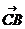 .
.
 (-1-1;0-0;4-4) = (-2;0;0)
(-1-1;0-0;4-4) = (-2;0;0)
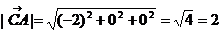
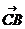 (0-1;-1-0;3-4) = (-1;-1;-1)
(0-1;-1-0;3-4) = (-1;-1;-1)
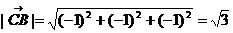
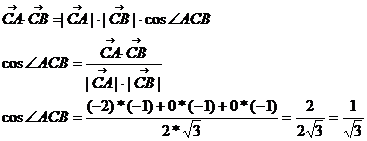
4. Вычислить интеграл 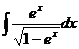 .
.
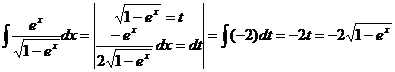
БИЛЕТ № 3.
Обратная матрица. Формула для нахождения обратной матрицы.
Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:
XA = AX = E,
где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А-1.
Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.
Общий подход к нахождению обратной матрицы.
Исходя из определения произведения матриц, можно записать:
AX = E Þ 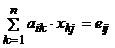 , i=(1,n), j=(1,n),
, i=(1,n), j=(1,n),
eij = 0, i ¹ j,
eij = 1, i = j .
Таким образом, получаем систему уравнений:
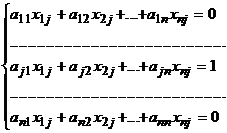 ,
,
Решив эту систему, находим элементы матрицы Х.
Но такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
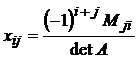
где Мji – дополнительный минор элемента аji матрицы А.
Лежат ли точки А (-1;2;-1), В (0;-1;0) и Д (1;-8;7) на одной прямой? Ответ обосновать. Найти длину отрезка АД.
Составим уравнение прямой АД:
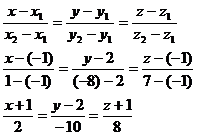
Проверим точку В:
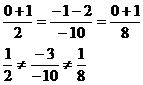
Значит точки А, В и Д не лежат на одной прямой.
Длина отрезка АД:
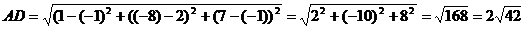
4. Вычислить интеграл 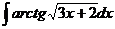
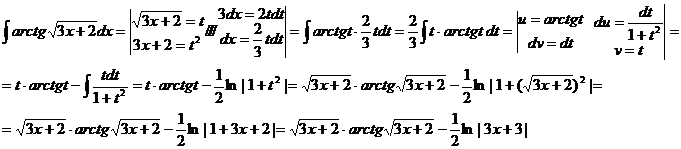
БИЛЕТ № 4.
Формулы Крамера.
Система из n уравнений с n неизвестными
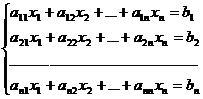
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, где
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
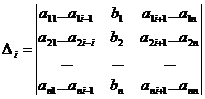
БИЛЕТ № 5.
Метод Гаусса.
Метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:
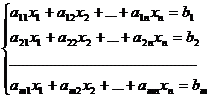
Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения и т.д.
Получим:
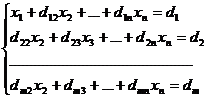 ,
,
где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
БИЛЕТ № 6.
БИЛЕТ № 7.
БИЛЕТ № 8.
БИЛЕТ № 9.
1. Линейно зависимые и линейно независимые системы векторов в пространстве R2 и R3.
Система векторов 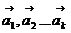 называется линейно зависимой, если существуют числа
называется линейно зависимой, если существуют числа 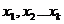 , не равные нулю одновременно, такие, что
, не равные нулю одновременно, такие, что 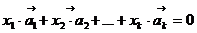 .
.
Если последнее равенство выполняется только при 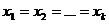 , система векторов называется линейно независимой.
, система векторов называется линейно независимой.
В пространстве Rn любая система, содержащая более чем n векторов, линейно зависима.
Линейную зависимость системы векторов 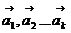 из Rn можно установить следующим образом. Сравнивая координаты векторов из левой и правой части векторного равенства
из Rn можно установить следующим образом. Сравнивая координаты векторов из левой и правой части векторного равенства 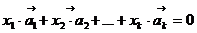 , получим однородную систему уравнений. Система векторов
, получим однородную систему уравнений. Система векторов 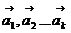 линейно зависима тогда и только тогда, когда получившаяся однородная система линейных уравнений имеет ненулевое решение.
линейно зависима тогда и только тогда, когда получившаяся однородная система линейных уравнений имеет ненулевое решение.
БИЛЕТ № 10.
Базис. Координаты вектора.
Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.
Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.
Базисом на прямой называется любой ненулевой вектор.
Если 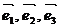 - базис в пространстве и
- базис в пространстве и 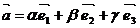 , то числа a, b и g - называются компонентами или координатами вектора
, то числа a, b и g - называются компонентами или координатами вектора 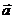 в этом базисе.
в этом базисе.
В связи с этим можно записать следующие свойства:
- равные векторы имеют одинаковые координаты,
- при умножении вектора на число его компоненты тоже умножаются на это число,
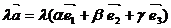 =
= 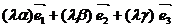 .
.
- при сложении векторов складываются их соответствующие компоненты.
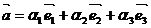 ;
; 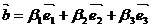 ;
; 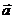 +
+ 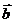 =
= 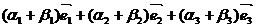 .
.
БИЛЕТ № 11.
1. Преобразование координат вектора при переходе к новому базису.
Пусть в 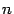 -мерном линейном пространстве
-мерном линейном пространстве 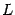 выбран базис
выбран базис 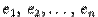 , и другой, новый, базис
, и другой, новый, базис 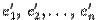 . Возьмем произвольный вектор
. Возьмем произвольный вектор 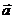 из пространства
из пространства 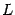 . Его координатный столбец в старом базисе обозначим
. Его координатный столбец в старом базисе обозначим 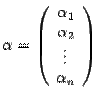 , а в новом --
, а в новом -- 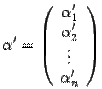 .
.
Запишем разложения новых базисных векторов по старому базису:
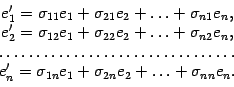
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса 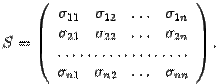
Эта матрица называется матрицей перехода от старого базиса к новому.
Координатные столбцы в старом базисе и в новом базисе связаны формулой 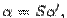 где справа стоит произведение матрицы перехода
где справа стоит произведение матрицы перехода 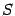 на матрицу-столбец.
на матрицу-столбец.
Доказательство. Так как 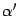 - координатный столбец вектора
- координатный столбец вектора 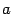 в новом базисе, то
в новом базисе, то 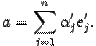 . Заменив векторы
. Заменив векторы 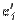 их разложениями по старому базису, получим:
их разложениями по старому базису, получим: 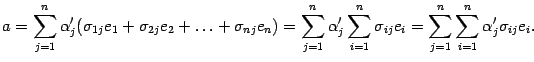 .
.
Изменим порядок суммирования 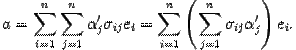 Здесь мы получили разложение вектора
Здесь мы получили разложение вектора 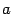 по старому базису, причем координата вектора с номером
по старому базису, причем координата вектора с номером 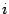 равна
равна 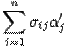 . Элемент с номером
. Элемент с номером 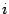 столбца
столбца 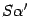 будет иметь такой же вид. Следовательно, формула доказана.
будет иметь такой же вид. Следовательно, формула доказана.
БИЛЕТ № 12.
БИЛЕТ № 13.
БИЛЕТ № 14.
БИЛЕТ № 15.
БИЛЕТ № 16.
Определение производной. Таблица производных.
Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке хo называется предел 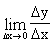 =
= 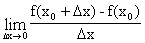 .
.
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке xo; при этом она оказывается обязательно и непрерывной в этой точке.
Если же рассматриваемый предел равен ∞ (или -∞ ), то при условии, что функция в точке хo непрерывна, будем говорить, что функция f(x) имеет в точке хo бесконечную производную.
Производная обозначается символами y ' , f ' (xo), 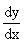 ,
, 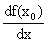 .
.
Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том, что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке хo; физический смысл - в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент t0.
Таблица производных:
1. (um)' = m um-1 u' (m принадлежит R1 )
2. (au)' = au lna× u'.
3. (eu)' = eu u'.
4. (loga u)' = u'/(u ln a).
5. (ln u)' = u'/u.
6. (sin u)' = cos u× u'.
7. (cos u)' = - sin u× u'.
8. (tg u)' = 1/ cos2u× u'.
9. (ctg u)' = - u' / sin2u.
10. (arcsin u)' = u' / 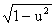 .
.
11. (arccos u)' = - u' / 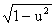 .
.
12. (arctg u)' = u'/(1 + u2).
13. (arcctg u)' = - u'/(1 + u2).
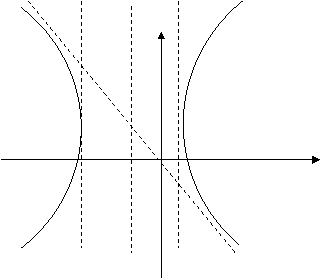
3. Привести уравнение 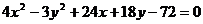 к каноническому виду, определить вид кривой и построить её.
к каноническому виду, определить вид кривой и построить её.
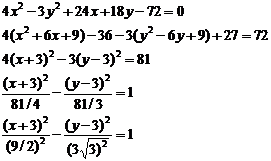
 Вид кривой – гипербола.
Вид кривой – гипербола.
 |
y
 | |
 | |
 |
3+ 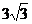
-15/2 3/2
-3 0 x
3 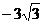
4. Зависимость у от х задана параметрически 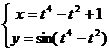 . Найти
. Найти 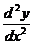 .
.
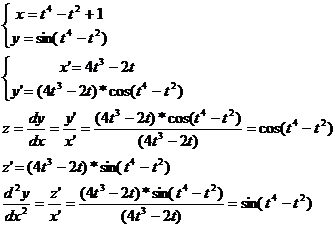
БИЛЕТ № 17.
БИЛЕТ № 18.
Теорема Ролля.
Теорема. Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (а, b) и значения функции на концах отрезка равны f(a) = f(b), то на интервале (а, b) существует точка e, a < e < b, в которой производная функция f(x) равная нулю,
f¢(e) = 0.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале (a, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна оси Ох. Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.
Доказательство. По свойству функций, непрерывных на отрезке функция f(x) на отрезке [a, b] принимает наибольшее и наименьшее значения. Обозначим эти значения М и m соответственно. Возможны два различных случая М = m и M ¹ m.
1. Пусть M = m. Тогда функция f(x) на отрезке [a, b] сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за e можно принять любую точку интервала.
2. Пусть М = m. Так значения на концах отрезка равны, то хотя бы одно из значений М или m функция принимает внутри отрезка [a, b]. Обозначим e, a < e < b точку, в которой f(e) = M. Так как М- наибольшее значение функции, то для любого Dх ( будем считать, что точка e + Dх находится внутри рассматриваемого интервала) верно неравенство:
Df(e) = f(e + Dx) – f(e) £ 0
При этом 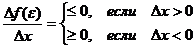
Но так как по условию производная в точке e существует, то существует и предел 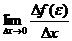 .
.
Т.к. 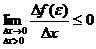 и
и 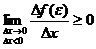 , то можно сделать вывод:
, то можно сделать вывод: 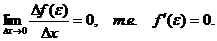
Теорема доказана.
Теорема Ролля имеет несколько следствий:
1) Если функция f(x) на отрезке [a, b] удовлетворяет теореме Ролля, причем
f(a) = f(b) = 0, то существует по крайней мере одна точка e, a < e < b, такая, что f¢(e) = 0. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.
2) Если на рассматриваемом интервале (а, b) функция f(x) имеет производную (n-1)- го порядка и n раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная (n – 1) – го порядка равна нулю.
3. Вычислить координаты вектора 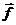 , перпендикулярного вектору
, перпендикулярного вектору 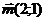 , если
, если 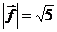 .
.
Воспользуемся формулой скалярного произведения векторов:
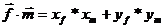
Так как векторы перпендикулярны, то 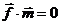 . Получим систему уравнений:
. Получим систему уравнений:
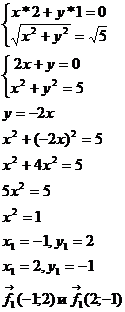
4. Вычислить 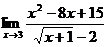 .
.
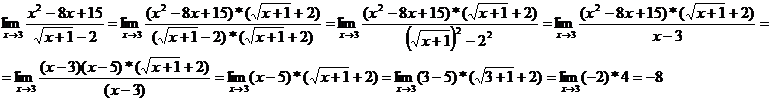
БИЛЕТ № 19.
Теорема Коши.
Если функции f(x) и g(x) непрерывны на отрезке [a, b] и дифференцируемы на интервале (a, b) и g¢(x) ¹ 0 на интервале (a, b), то существует по крайней мере одна точка e, a < e < b, такая, что
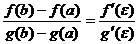 .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке e.
Доказательство. Рассмотрим вспомогательную функцию
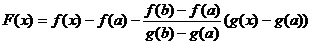 ,
,
которая на интервале [a, b] удовлетворяет условиям теоремы Ролля. Легко видеть, что при х = а и х = b F(a) = F(b) = 0. Тогда по теореме Ролля существует такая точка e,
a < e < b, такая, что F¢(e) = 0.
Т.к. 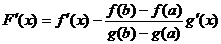 , то
, то 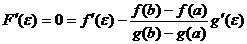
А т.к. 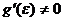 , то
, то 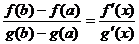 . Теорема доказана.
. Теорема доказана.
3. Построить геометрическое место точек плоскости хОу, задаваемое уравнением 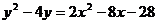 .
.
Приведём уравнение кривой к каноническому виду:

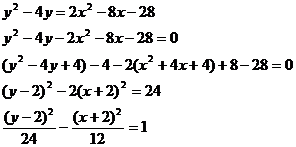
Уравнение сопряжённой гиперболы.
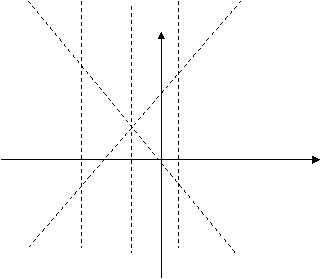 |
y
 | |
 | |
 |
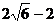
-2 0 x
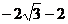
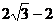

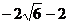
4. Провести исследование и построить график функции 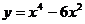 .
.
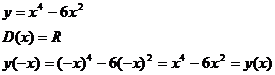
Функция чётная, симметрична относительно Ох.
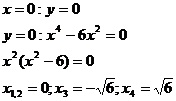
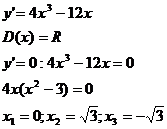


 y’ - + - +
y’ - + - +


 y
y  0
0  x
x
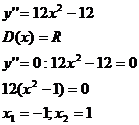


 y’’ + - +
y’’ + - +

 y -1 1 x
y -1 1 x
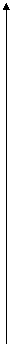 y
y
 | |||
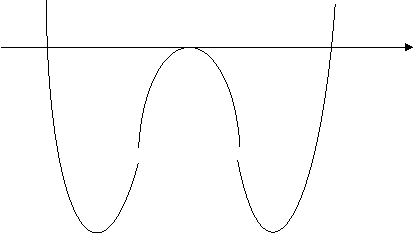 |
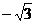 -1 0 1
-1 0 1 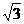
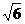 x
x
-5
-9
БИЛЕТ № 20.
Теорема Лагранжа.
Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется по крайней мере одна точка e, a < e < b, такая, что 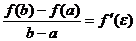 .
.
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Отношение 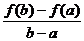 равно угловому коэффициенту секущей АВ.
равно угловому коэффициенту секущей АВ.
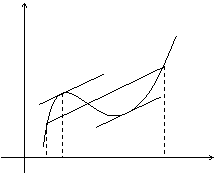 у
у
В
А
0 а e b x
Если функция f(x) удовлетворяет условиям теоремы, то на интервале (а, b) существует точка e такая, что в соответствующей точке кривой y = f(x) касательная параллельна секущей, соединяющей точки А и В. Таких точек может быть и несколько, но одна существует точно.
Доказательство. Рассмотрим некоторую вспомогательную функцию
F(x) = f(x) – yсек АВ
Уравнение секущей АВ можно записать в виде:

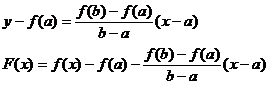
Функция F(x) удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b). По теореме Ролля существует хотя бы одна точка e, a < e < b, такая что F¢(e) = 0.
Т.к. 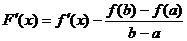 , то
, то 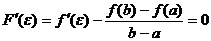 , следовательно
, следовательно
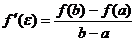
Теорема доказана.
3. Вычислить интеграл 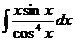 .
.
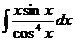
4. Вычислить 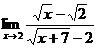 .
.
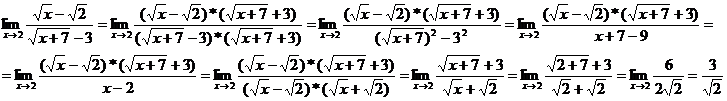
БИЛЕТ № 21.
БИЛЕТ № 22.
1. Приведение уравнения кривой второго порядка к каноническому виду (без поворотов).
Кривая второго порядка может быть задана уравнением
Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0.
1. Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.
2. 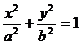 - уравнение эллипса.
- уравнение эллипса.
3. 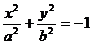 - уравнение “мнимого” эллипса.
- уравнение “мнимого” эллипса.
4. 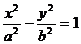 - уравнение гиперболы.
- уравнение гиперболы.
5. a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых.
6. y2 = 2px – уравнение параболы.
7. y2 – a2 = 0 – уравнение двух параллельных прямых.
8. y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых.
9. y2 = 0 – пара совпадающих прямых.
10. (x – a)2 + (y – b)2 = R2 – уравнение окружности.
Билет № 23.
Правило Лопиталя.
Теорема (правило Лопиталя). Если функции f(x) и g(x) дифференцируемы в вблизи точки а, непрерывны в точке а, g¢(x) отлична от нуля вблизи а и f(a) = g(a) = 0, то предел отношения функций при х®а равен пределу отношения их производных, если этот предел (конечный или бесконечный) существует.
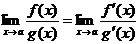
Доказательство. Применив формулу Коши, получим:
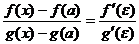
где e - точка, находящаяся между а и х. Учитывая, что f(a) = g(a) = 0:
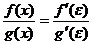
Пусть при х®а отношение 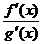 стремится к некоторому пределу. Т.к. точка e лежит между точками а и х, то при х®а получим e®а, а следовательно и отношение
стремится к некоторому пределу. Т.к. точка e лежит между точками а и х, то при х®а получим e®а, а следовательно и отношение 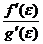 стремится к тому же пределу. Таким образом, можно записать:
стремится к тому же пределу. Таким образом, можно записать:
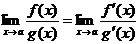 .
.
Теорема доказана.
Таблица эквивалентности бесконечно малых.
| 1) | 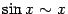 . . |
| 2) | 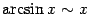 . . |
| 3) | 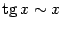 . . |
| 4) | 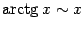 . . |
| 5) | 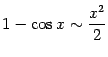 . . |
| 6) | 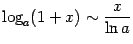 ( ). ( ). |
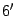 ) ) | 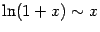 . . |
| 7) | 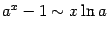 ( ). ( ). |
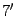 ) ) | 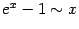 . . |
3. Вычислить интеграл 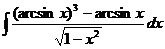 .
.
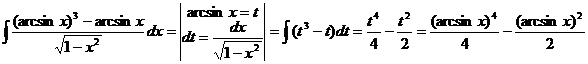
БИЛЕТ № 24.
БИЛЕТ № 1.
Линейные операции над матрицами. Умножение матриц.
Матрицей размера m´n, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 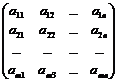
Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.
cij = aij ± bij
С = А + В = В + А.
Операция умножения матрицы любого размера на произвольное число сводится к умножению каждого элемента матрицы на это число.
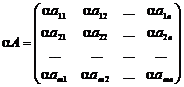
a (А+В) =aА ± aВ
А(a±b) = aА ± bА
Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам: A×B = C; 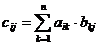 .
.
Из определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц:
1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
А×Е = Е×А = А
Очевидно, что для любых матриц выполняются следующее свойство:
A×O = O; O×A = O,
где О – нулевая матрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа a верно соотношение:
a(AB) = (aA)B = A(aB).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Для любых квадратных матриц det (AB) = detA×detB.
2. Неопределённый интеграл. Определение, таблица.
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C.
Записывают: 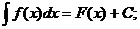
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
| Интеграл | Значение | Интеграл | Значение | ||
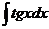 | -ln½cosx½+C | 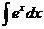 | ex + C | ||
 | ln½sinx½+ C | 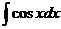 | sinx + C | ||
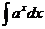 | 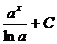 | 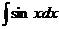 | -cosx + C | ||
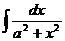 | 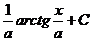 | 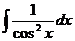 | tgx + C | ||
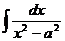 | 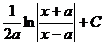 | 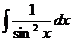 | -ctgx + C | ||
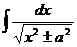 | ln 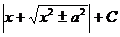 | 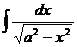 | arcsin  + C + C | ||
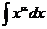 | 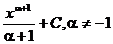 | 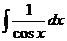 | 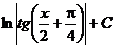 | ||
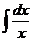 | 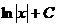 | 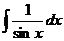 | 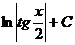 |
