Функция распределения случайной величины
Случайную величину 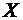 можно характеризовать не только законом распределения. Закон распределения характеризует вероятности событий
можно характеризовать не только законом распределения. Закон распределения характеризует вероятности событий 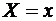 для разных
для разных 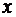 . Однако можно рассматривать вероятности события
. Однако можно рассматривать вероятности события 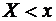 , где
, где 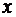 - текущая переменная. Под выражением
- текущая переменная. Под выражением 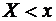 понимается событие «случайная величина
понимается событие «случайная величина 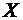 приняла значение меньшее
приняла значение меньшее 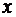 ». Вероятность
». Вероятность 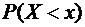 является некоторой функцией от
является некоторой функцией от 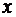 , которая называется функцией распределения.
, которая называется функцией распределения.
Функцией распределения случайной величины 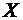 называется функция
называется функция 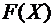 , равная вероятности
, равная вероятности 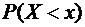 того, что случайная величина приняла значение, меньшее
того, что случайная величина приняла значение, меньшее 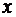 .
.
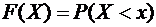
Функцию распределения 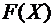 иногда называют интегральной функцией распределения или интегральным законом распределения.
иногда называют интегральной функцией распределения или интегральным законом распределения.
Функция распределения полностью характеризует случайную величину с вероятностной точки зрения. Функция распределения существует как для дискретных, так и для непрерывных случайных величин.
Свойства функции распределения.
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей
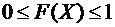
2. Функция распределения случайной величины есть неубывающая функция, т.е. если 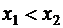 , то
, то 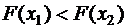 .
.
3. Вероятность попадания случайной величины в интервал 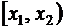 равна приращению ее функции распределения на этом интервале, т.е.
равна приращению ее функции распределения на этом интервале, т.е.
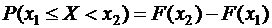
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ПЛОТНОСТЬ ВЕРОЯТНОСТИ
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.
Для непрерывной случайной величины можно дать еще одно определение:
Случайная величина 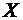 называется непрерывной, если ее функция распределения непрерывно в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
называется непрерывной, если ее функция распределения непрерывно в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.
Непрерывную случайную величину 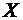 можно задать не только с помощью функции распределения
можно задать не только с помощью функции распределения 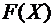 , но и с помощью плотности вероятности.
, но и с помощью плотности вероятности.
Плотностью вероятности (плотностью распределения) 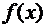 непрерывной случайной величины
непрерывной случайной величины 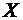 называется производная ее функции распределения
называется производная ее функции распределения
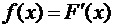
Иногда функцию 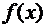 называют дифференциальной функцией распределения или дифференциальным законом распределения.
называют дифференциальной функцией распределения или дифференциальным законом распределения.
График плотности вероятности 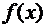 называют кривой распределения. Кривая распределения лежит не ниже оси абсцисс, и площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
называют кривой распределения. Кривая распределения лежит не ниже оси абсцисс, и площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.
Свойства плотности вероятности непрерывной случайной величины
1. Плотность вероятности – неотрицательная функция
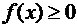 .
.
2. Вероятность попадания непрерывной случайной величины в интервал 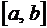 равна определенному интегралу от ее плотности вероятности в пределах от
равна определенному интегралу от ее плотности вероятности в пределах от 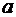 до
до 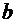
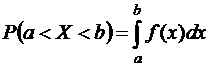
3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле
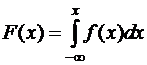 .
.
