Дискретные и непрерывные случайные величины

ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Случайной величиной называется переменная, которая в результате испытания принимает одно и только одно возможное значение, но какое именно – заранее не известно.

Примеры случайных величин:

- количество студентов на лекции;

- количество больных в городе;

- число родившихся в течение суток в г. Кемерово;

- продолжительность человеческой жизни.

Случайные величины принято обозначать прописными латинскими буквами X, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z,…

Вероятности случайных величин обозначают буквами с соответствующими индексами 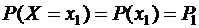- запись показывает вероятность того, что случайная величина принимает значение .

Случайные величины разделяют на дискретные и непрерывные.

Дискретной называют случайную величину, принимающую отдельные друг от друга возможные значения, которые можно пронумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.

Например,

- количество мальчиков, родившихся в каком-либо месяце;

- количество рецептов, поступивших в аптеку в течение дня;

- число ударов пульса больного в минуту;

- количество осложнений после операций в данной больнице.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала. Число возможных значений непрерывной случайной величины бесконечно.

Например,

- температура воздуха в течение дня;

- продолжительность человеческой жизни;

- время инкубационного периода заболевания.

ДИСКРЕТНАЯ СЛУЧАЙНАЯ ВЕЛИЧИНА

НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ПЛОТНОСТЬ ВЕРОЯТНОСТИ

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала.

Для непрерывной случайной величины можно дать еще одно определение:

Случайная величина называется непрерывной, если ее функция распределения непрерывно в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Непрерывную случайную величину 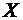можно задать не только с помощью функции распределения 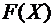, но и с помощью плотности вероятности.

Плотностью вероятности (плотностью распределения) 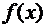непрерывной случайной величины 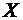называется производная ее функции распределения

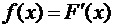
Иногда функцию 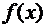называют дифференциальной функцией распределения или дифференциальным законом распределения.

График плотности вероятности 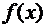называют кривой распределения. Кривая распределения лежит не ниже оси абсцисс, и площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Свойства плотности вероятности непрерывной случайной величины

1. Плотность вероятности – неотрицательная функция

.

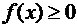2. Вероятность попадания непрерывной случайной величины в интервал 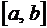равна определенному интегралу от ее плотности вероятности в пределах от 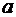до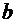

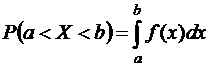
3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле

.

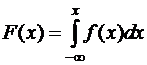ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Случайной величиной называется переменная, которая в результате испытания принимает одно и только одно возможное значение, но какое именно – заранее не известно.

Примеры случайных величин:

- количество студентов на лекции;

- количество больных в городе;

- число родившихся в течение суток в г. Кемерово;

- продолжительность человеческой жизни.

Случайные величины принято обозначать прописными латинскими буквами X, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z,…

Вероятности случайных величин обозначают буквами с соответствующими индексами 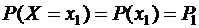- запись показывает вероятность того, что случайная величина 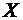принимает значение .

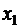Случайные величины разделяют на дискретные и непрерывные.

Дискретной называют случайную величину, принимающую отдельные друг от друга возможные значения, которые можно пронумеровать. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.

Например,

- количество мальчиков, родившихся в каком-либо месяце;

- количество рецептов, поступивших в аптеку в течение дня;

- число ударов пульса больного в минуту;

- количество осложнений после операций в данной больнице.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного интервала. Число возможных значений непрерывной случайной величины бесконечно.

Например,

- температура воздуха в течение дня;

- продолжительность человеческой жизни;

- время инкубационного периода заболевания.