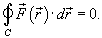Объем тела, образованного вращением замкнутой кривой относительно оси Ox

Предположим, что область R расположена в верхней полуплоскости y ≥ 0 и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C, обход которой осуществляется против часовой стрелки. В результате вращения области R вокруг оси Ox образуется тело Ω (рисунок 2). Объем данного тела определяется формулами

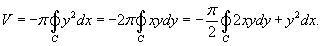
Криволинейные интегралы 2 рода

Предположим, что кривая C задана векторной функцией 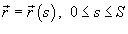, где переменная s − длина дуги кривой. Тогда производная векторной функции

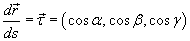
представляет собой единичный вектор, направленный вдоль касательной к данной кривой

Введем векторную функцию 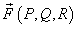, определенную на кривой C, так, чтобы для скалярной функции

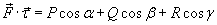
существовал криволинейный интеграл 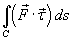. Такой интеграл 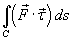называется криволинейным интегралом второго рода от векторной функции 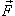вдоль кривой C и обозначается как

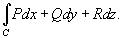
Таким образом, по определению,

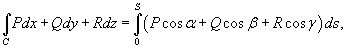
где 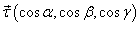− единичный вектор касательной к кривой C.

Последнюю формулу можно переписать также в векторной форме:

где .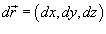

Если кривая C лежит в плоскости Oxy, то полагая R = 0, получаем

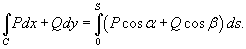
Свойства криволинейного интеграла второго рода

Криволинейный интеграл II рода обладает следующими свойствами:

1.Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −Cкривую противоположного направления - от B к A. Тогда

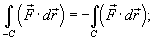
2.Если C − объединение кривых C₁ и C₂ то

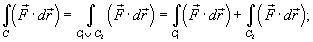
3.Если кривая C задана параметрически в виде 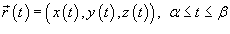, то

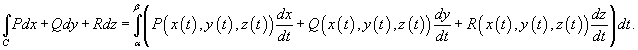
4.Если кривая C лежит в плоскости Oxy и задана уравнением 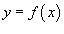(предполагается, что R =0и t = x), то последняя формула записывается в виде

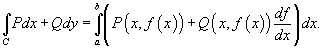
Восстановление функции 2,3 переменных по ее дифференциалу

.

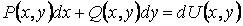Найти функцию 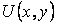по ее полному дифференциалу 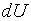можно, например, с помощью криволинейного интеграла II рода, вычислив его от 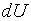по линии, соединяющей фиксированную точку (x₀,y₀) и переменную точку (x;y) (Рис. 18):

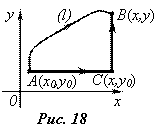
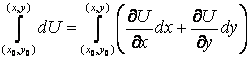
записываем параметрические уравнения любой линии l: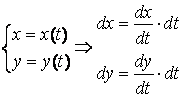

и сводим криволинейный интеграл к определённому интегралу

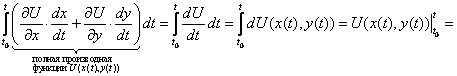
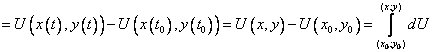
Таким образом получено, что криволинейный интеграл II рода от полного дифференциала dU(x,y) равен разности значений функции U(x,y) в конечной и начальной точках линии интегрирования.

Зная теперь это результат, нужно подставить вместо dU в криволинейный интеграл выражение 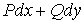и провести вычисление интеграла по ломаной (ACB), учитывая его независимость от формы линии интегрирования:

на (AC): 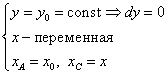на (СВ) :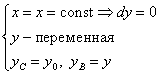

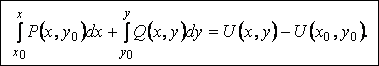
Таким образом, получена формула, с помощью которой восстанавливается функция 2-х переменных 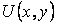по ее полному дифференциалу .

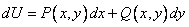Приложение формулы Грина для выч криволин интегр и площади

Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция

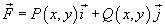
Тогда справедлива формула Грина

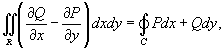
Если 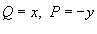, то формула Грина принимает вид

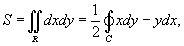
где S − это площадь области R, ограниченной контуром C.

24.Независимость пути интегрирования кринтегр 2 рода

Криволинейный интеграл второго рода от векторной функции 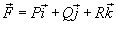не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция 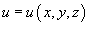, такая, что

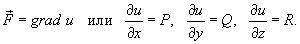
В этом случае криволинейный интеграл второго рода от функции 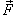вдоль кривой C от точки A до точки Bвыражается формулой

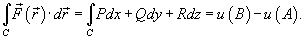
Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение