Законы движения точек механизма

Координаты точек А, В, C₁, соответственно, равны

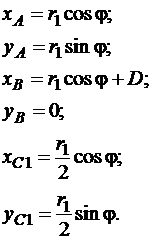
Определим координаты центра шатуна АВ – точки С₃

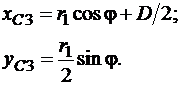
Зная координаты точек А, В и С₃ , можно построить изображение механизма в любой момент времени и определить траекторию точки С₃.

АЛГОРИТМ РАСЧЕТА

КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК

Скорости точек А, В, С₁, С₃ определяются как производные по времени от координат соответствующих точек.

Для каждой точки следует найти проекции скорости на координатные оси и модуль скорости

;

;

.

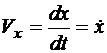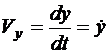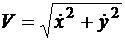Ускорения точек механизма определяются как вторые производные по времени от координат, или первые производные от скоростей соответствующих точек. Для каждой точки следует определить проекции ускорения и модуль ускорения

;

;

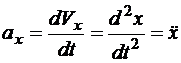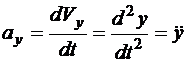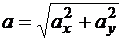
Для шатуна АВ можно определить первую и вторую производную по времени от угла поворота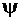

;

.

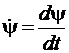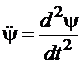АНАЛИТИЧЕСКИЙ РАСЧЕТ КИНЕМАТИКИ

КРИВОШИПНО-КУЛИСНОГО МЕХАНИЗМА

ЗАДАЧА.

Угол поворота кривошипа ОА кривошипно-кулисного механизма (рис. 2) изменяется по закону φ = φ₁(t). Длина звеньев ОА, О₁В и межосевое расстояние OO₁ известны (таблица 2).

Определить координаты точек А и С₁, С₂, лежащих в середине кривошипа ОА и кулисы O₁B в неподвижной декартовой системе ко­ординат, а также проекции скорости и скорость, проекции ускорения и ускорение точек А, С₁ и C₂ в положении механизма, соответствующем заданному углу поворота кривошипа.

Исходные данные представлены в таблице 2.

При расчете можно воспользоваться программой Mathcad.

Таблица 2

Номер варианта	Закон движения кривошипа	ОА, м	АВ, м	OO1, м	ω0, рад/с	ε1, рад/с	b
1.1 – 1.35	φ = ω0t + + ε1t2/2	0,3	0,8	0,4			–
2.1 – 2.35	0,4	0,9	0,3			–
3.1 – 3.35	0,5	1,4	0,7			–
4.1 – 4.35	φ = 2π sin bt	0,3	1,0	0,5	–	–	π/6
5.1 – 5.35	0,4	1,2	0,6	–	–	π/4
6.1 – 6.35	0,5	1,0	0,3	–	–	π/3
7.1 – 7.35	φ = 2π cos bt	0,4	1,2	0,6	–	–
8.1 – 8.35	0,3	1,0	0,6	–	–
9.1 – 9.35	0,6	0,6	0,3	–	–

Примечание: вторая цифра номера варианта соответствует углу поворота кривошипа (1 – φ₁ = 10⁰, 2 – φ₁ = 20⁰, …, 35 – φ₁ = 350⁰).

ПРИМЕР РАСЧЕТА

В кривошипно-кулисном механизме (рис. 2) конец кривошипа АО скользит вместе с ползуном А вдоль кулисы ВО₁. Расстояние меж­ду осями валов О и О₁равно r₀, длина кривошипа АО равна r₁длина кулисы ВО₁равна 1. Кривошип вращается вокруг оси Оz по закону

1) φ₁ =φ₀ +ω₀t + ε₁t² / 2;

2) φ_l= asinbt

3) φ₁ = acosbt.

Определим координаты, скорости и ускорения точек А, С₁, С₂механизма в положении, соответствующем углу поворота кривошипа АО φ₁ = φ(t).

Рис. 2

Выразим все кинематические характеристики звеньев механизма через угол поворота кривошипа АО. Для этого составим векторное уравнение контура механизма

Проецируем это уравнение на оси неподвижной декартовой сис­темы координат Ох и Оу

r₁ cosφ₁ = r₂ cosφ₂,

r₀ + r₁ sinφ₁ = r₂ sinφ₂.

Определим неизвестные величины

.

Выразим

и при расчете сравним результаты с целью проверки.

ЗАКОНЫ ДВИЖЕНИЯ ТОЧЕК МЕХАНИЗМА

Определим координаты точек А, С₁, С₂ механизма

x_A = r₁ cosφ₁,

y_A = r₁ sinφ₁;

x_C1 = x_A/2,

y_C1 = y_A/2;

x_C2 = l cosφ₂ /2,

y_C2 = l sinφ₂ /2 – r₀.

АЛГОРИТМ РАСЧЕТА