Задача 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах: 1,3,5,7,11,12.
Содержание
Задача 1. Для заданных множеств А, В и С найдите: 2
Задача 2. Даны отображения (числовые функции) ƒ и g.. 5
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах.. 8
Задача 4.Определить к каким классам относится функция…… 9
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ: 10
Задача 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах.. 11
Задача 7. Используя метод Квайна – Мак-Класки, необходимо найти МДНФ функции, принимающей. 13
Задача 8. Используя метод диаграмм Вейча, необходимо найти МДНФ функции, принимающей значение 1 15
Задача 9. Задать граф. 17
Задача 10. Определить следующие основные характеристики графа: 18
Задача 11. Определить, является ли данный граф: 19
Задача 12. Определить метрические характеристики графа. 21
Список литературы.. 23
Задача 1. Для заданных множествА, В и С найдите:
АÈВ, АÈС, ВÈС, АÈВÈС, АÇВ, АÇС, ВÇС, АÇВÇС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразите на плоскостиА´В, А´С, В´С. Найдите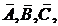 
считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
А = [-3; 0] – отрезок числовой оси
В = (-1; 3] – полуинтервал на числовой оси
С = (-0.5; 4) – интервал на числовой оси
Решение:
Объединением двух множеств A и B называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B, поэтому:
АÈВ =[-3;3]
АÈС=[-3;4)
ВÈС=(-1; 4)
АÈВÈС = [-3; 4)
Пересечением двух множеств A и B называется множество элементов, принадлежащих одновременно и A, и B, поэтому:
АÇВ = (-1;0]
АÇС= (-0,5;0]
ВÇС= (-0,5;3]
АÇВÇС= (-0,5;0]
Относительным дополнением множества B до множества A называется множество тех элементов A, которые не являются элементами B, поэтому
А \ В = [-3;-1]
B \ A= (0;3]
A \ C= [-3;-0,5]
C \ A= (0;4)
B \ C= (-1;-0,5]
C \ B= (3;4)
(А \ В) \ С= [-3;-1]
А \ (В \ С) = [-3;-1]
Симметрической разностью двух множеств A и B называется объединение двух разностейA\B и B\A, а абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, поэтому:
А Å B= (А \ В)È(В \ А)={[-3;-1], (0;3]}
А Å С = (А \ C)È(C \ А)={[-3;-0,5], (0;4)}
B Å C = (B \ C)È(C \ B)={(-1;-0,5], (3;4)}
A Å B Å C = ((AÅB)\C)È(C\(AÅB))={[-3;-1]}È{(-0,5;0],(3,4)}=
={[-3;-1],(-0,5;0],(3,4)}
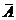={(-µ;-3),(0;+µ)}
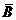={(-µ;-1],(3;+µ)}
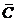={(-µ;-0,5],[4;+µ)}
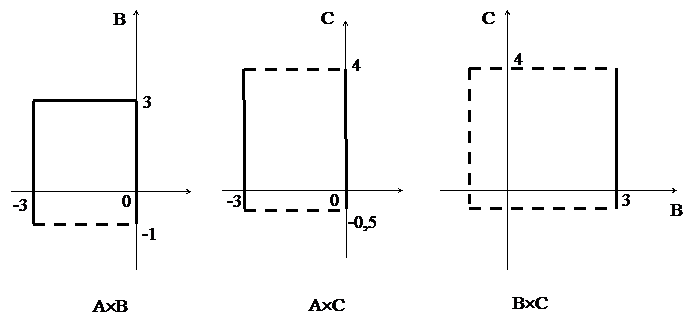Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что 
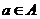и 
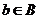, поэтому:
 | |||||
| |||||
| |||||
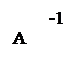Задача 2. Даны отображения (числовые функции) ƒ и g. Найдите область определения и область значений отображений. Определите, являются ли они инъективными, сюрьективными или биективными в найденных областях. Найдите композицию (ƒ ◦ g), (g ◦ ƒ), обратные (слева и справа) отображения: ƒ–1, g-1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найдите f(A), g(A),ƒ–1(B), g-1(B). Найдите также неподвижные точки отображений.
f(x) = –(x + 1)2; g(x) = –x –2; А = [–1.5; 1]; В = [–2; –1]
Решение:
область определения отображения f– это множество таких значений х, для которых имеется вещественное число у такое, что у=f(x). И, так как для любого вещественного числа х найдется число ус указанным свойством, то пр1f =ℝ – множество всех вещественных чисел.
Аналогично, область определения отображения g: пр1g =ℝ.
Область значений отображения f – это множество всех образов элементов хÎпр1f. Тем самым, пр2f ={yÎ ℝ.: y ≤ 0 } (т.к. (x + 1)2 ≥ 0 и =>–(x + 1)2 ≤ 0). А область значений отображения g – это множество всех вещественных чисел, т.е. пр2g =ℝ.
Отображение gявляется инъективным, поскольку для каждого уÎпр2g, имеется ровно один хÎ пр1g (или каждый образ имеет ровно один прообраз).
Отображение f инъективным не является, т.к. для некоторых уÎпр2f, имеется более одного прообраза, например: дляу= –1 прообразами будут х=0 и х= –2.
Отображение gявляется сюрьективным, поскольку для каждого уÎпр2g, имеется хотя бы один хÎпр1g (или каждый образ имеет хотя бы один прообраз).
Отображение f также является сюрьективным, т.к. для каждого уÎпр2f, имеется хотя бы один хÎпр1f такой, что у = f(x).
Так как gодновременно инъективно и сюрьективно, то оно является биективным отображением.
fнеявляется биективным отображением.
Найдем композицию отображений:
(f∘g)(x) = f(g(x)) =–(g(x)+1)2 =–(–x–2+1)2= –(–x–1)2=–(x+1)2,
(g∘f)(x) = g(f(x)) =–f(x)–2 = –(–(x+1)2) –2 =(x+1)2–2.
Отображение f обратимо справа, как сюрьекция. И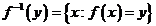 
, где y≤ 0. Из выражения y=–(x+1)2 найдем x.
Тогда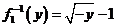 
и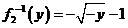 
, где y≤ 0.
При этом, (f∘f ‑1)(у)= f(f ‑1(y))=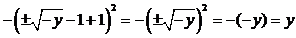 
– тождественное отображение при y ≤ 0.
Отображение g обратимо как слева, так и справа, как биекция. И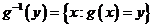 
, где y любое. Из выражения 
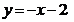следует: 
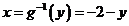. И при этом: (g∘g‑1 )(у) = g(g‑1(y)) = –(–2–y)–2 = y
и(g‑1∘g )(х) =g‑1(g(х)) = –2–(–x-2) = x – тождественные отображения.
Посвойствам композиции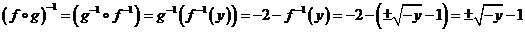 
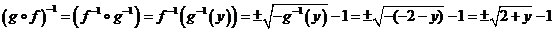
f(A) = {y = f(x), гдеxÎA }, поэтомуf(A)=[–4; –0,25].
Аналогично, g(A) = {y = g(x), где xÎA } = [–3; –0,5].
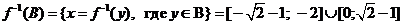
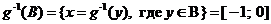
Найдем неподвижные точки. По определению это такиех, что: f(x)=x и g(x)=x. Таким образом, x = –(x+1)2. Отсюда x2+3x+1=0 и т. к. дискриминант D=9–4=5>0, то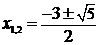 
– две неподвижные точки f(x).
Из g(x)=x следует, что x=–x–2 и x= –1 – неподвижная точка g(x).
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах:
x → (y ↓ z) = (x → y ) ↓ (x → z)
((x ≡ y) · (x | y)) ≡ x&y
Решение:
1. Составим таблицы истинности для функций
| x | y | z | (y ↓ z) | x → (y ↓ z) |
| x | y | z | (x → y ) | (x → z) | (x → y ) ↓ (x → z) |
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функции
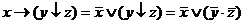
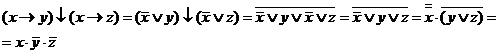
Так как полученные выражения не равны, то функции не эквивалентны.
2. Составим таблицы истинности для функций
| x | y | x&y |
| x | y | x ≡ y | x | y | (x ≡ y) · (x | y) |
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функцию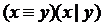 
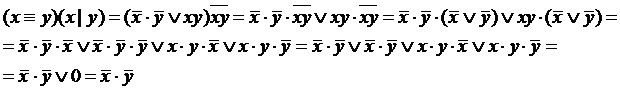
Так как выражения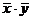 
и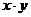 
не равны, то функции не эквивалентны.
Задача 4.Определить к каким классам относится функция следующего вида: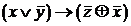 
Решение:
| x | y | z |  |  | |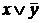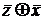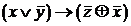
f(0,0,0) = 0 => функция принадлежит к классу Т0– классуфункций, сохраняющих 0,
f(1,1,1) ≠ 1=> функция не принадлежит кклассу Т1 – классу функций, сохраняющих 1,
f(0,0,0) ≠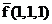 
=> функция не принадлежит к классуS– классу самодвойственных функций,
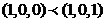, а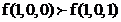 
=> функция не принадлежит к классу M – классу монотонных функций.
Составим для функции полином Жегалкина (методом неопределенных коэффициентов):
f=c0Åc1xÅc2yÅc3zÅc12xyÅc13xzÅc23yzÅc123xyz
f(0,0,0)= c0=0
f(0,0,1)= c0Åc3=1® c3=1
f(0,1,0)= c0Åc2=1® c2=1
f(0,1,1)= c0Åc2Åc3Åc23=1® c23=1
f(1,0,0)= c0Åc1=1® c1=1
f(1,0,1)= c0Åc1Åc3Åc13=0® c13=0
f(1,1,0)= c0Åc1Åc2Åc12=1® c12=1
f(1,1,1)= c0Åc1Åc2Åc3Åc12Åc13Åc23Åc123=0® c123=1
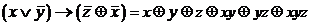
функция является линейной, если ее полином Жегалкина имеет вид:
f(x1,x2,…xn)=c0Åc1x1Åc2x2Å…Åcnxn
В нашем случае функция не приводится к такому виду => она не линейна и
не принадлежит к L– классу линейных функций.
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ, принимающей значения 1 на следующих наборах:
0, 1,2,6,8,12,13,14
Решение.
Составим таблицу истинности для функции. В столбце СДНФ показаны элементарные конъюнкции, в строках, где функция принимает единичные значения, а в столбце СКНФ - элементарные дизъюнкции в строках, где функция равна нулю.
| x1 | x2 | x3 | x4 | f | СДНФ | СКНФ |
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 |
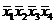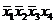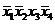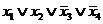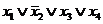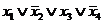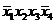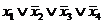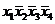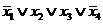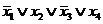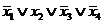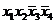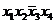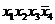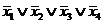Тем самым, совершенная дизъюнктивная нормальная форма (СДНФ):
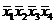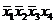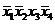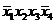f(x)= Ú 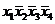Ú Ú 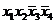Ú Ú 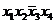Ú Ú .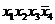
Совершенная конъюнктивная нормальная форма (СКНФ):
f(x)=( )&( )&( )&( )&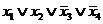
&( )&( )&( )&( )
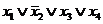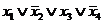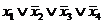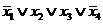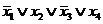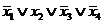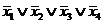Список литературы
1 Аляев Ю.А. Тюрин С.Ф. Дискретная математика и математическая логика. — М.: Финансы и статистика, 2006. — 368 с.
2 Акимов О.Е.Дискретная математика. Логика, группы, графы. - 2-е изд.- М., Лаборатория базовых знаний, 2001. - 376 с. - "Технический университет".
3 Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2006, 288 стр.
4 Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике: Учеб. пособие. — 3-е изд., перераб. — М.: ФИЗМАТЛИТ, 2005. - 416 с.
5 Яблонский С.В. Введение в дискретную математику. 4-е издание, стереотипное - М.: Высшая школа, 2005. - 484 с
Содержание
Задача 1. Для заданных множеств А, В и С найдите: 2
Задача 2. Даны отображения (числовые функции) ƒ и g.. 5
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах.. 8
Задача 4.Определить к каким классам относится функция…… 9
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ: 10
Задача 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах.. 11
Задача 7. Используя метод Квайна – Мак-Класки, необходимо найти МДНФ функции, принимающей. 13
Задача 8. Используя метод диаграмм Вейча, необходимо найти МДНФ функции, принимающей значение 1 15
Задача 9. Задать граф. 17
Задача 10. Определить следующие основные характеристики графа: 18
Задача 11. Определить, является ли данный граф: 19
Задача 12. Определить метрические характеристики графа. 21
Список литературы.. 23
Задача 1. Для заданных множествА, В и С найдите:
АÈВ, АÈС, ВÈС, АÈВÈС, АÇВ, АÇС, ВÇС, АÇВÇС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразите на плоскостиА´В, А´С, В´С. Найдите 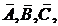считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
А = [-3; 0] – отрезок числовой оси
В = (-1; 3] – полуинтервал на числовой оси
С = (-0.5; 4) – интервал на числовой оси
Решение:
Объединением двух множеств A и B называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B, поэтому:
АÈВ =[-3;3]
АÈС=[-3;4)
ВÈС=(-1; 4)
АÈВÈС = [-3; 4)
Пересечением двух множеств A и B называется множество элементов, принадлежащих одновременно и A, и B, поэтому:
АÇВ = (-1;0]
АÇС= (-0,5;0]
ВÇС= (-0,5;3]
АÇВÇС= (-0,5;0]
Относительным дополнением множества B до множества A называется множество тех элементов A, которые не являются элементами B, поэтому
А \ В = [-3;-1]
B \ A= (0;3]
A \ C= [-3;-0,5]
C \ A= (0;4)
B \ C= (-1;-0,5]
C \ B= (3;4)
(А \ В) \ С= [-3;-1]
А \ (В \ С) = [-3;-1]
Симметрической разностью двух множеств A и B называется объединение двух разностейA\B и B\A, а абсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, поэтому:
А Å B= (А \ В)È(В \ А)={[-3;-1], (0;3]}
А Å С = (А \ C)È(C \ А)={[-3;-0,5], (0;4)}
B Å C = (B \ C)È(C \ B)={(-1;-0,5], (3;4)}
A Å B Å C = ((AÅB)\C)È(C\(AÅB))={[-3;-1]}È{(-0,5;0],(3,4)}=
={[-3;-1],(-0,5;0],(3,4)}
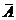={(-µ;-3),(0;+µ)}
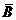={(-µ;-1],(3;+µ)}
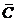={(-µ;-0,5],[4;+µ)}
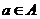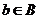Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что и , поэтому:
| | |||||
| |||||
| |||||
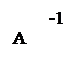Задача 2. Даны отображения (числовые функции) ƒ и g. Найдите область определения и область значений отображений. Определите, являются ли они инъективными, сюрьективными или биективными в найденных областях. Найдите композицию (ƒ ◦ g), (g ◦ ƒ), обратные (слева и справа) отображения: ƒ–1, g-1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найдите f(A), g(A),ƒ–1(B), g-1(B). Найдите также неподвижные точки отображений.
f(x) = –(x + 1)2; g(x) = –x –2; А = [–1.5; 1]; В = [–2; –1]
Решение:
область определения отображения f– это множество таких значений х, для которых имеется вещественное число у такое, что у=f(x). И, так как для любого вещественного числа х найдется число ус указанным свойством, то пр1f =ℝ – множество всех вещественных чисел.
Аналогично, область определения отображения g: пр1g =ℝ.
Область значений отображения f – это множество всех образов элементов хÎпр1f. Тем самым, пр2f ={yÎ ℝ.: y ≤ 0 } (т.к. (x + 1)2 ≥ 0 и =>–(x + 1)2 ≤ 0). А область значений отображения g – это множество всех вещественных чисел, т.е. пр2g =ℝ.
Отображение gявляется инъективным, поскольку для каждого уÎпр2g, имеется ровно один хÎ пр1g (или каждый образ имеет ровно один прообраз).
Отображение f инъективным не является, т.к. для некоторых уÎпр2f, имеется более одного прообраза, например: дляу= –1 прообразами будут х=0 и х= –2.
Отображение gявляется сюрьективным, поскольку для каждого уÎпр2g, имеется хотя бы один хÎпр1g (или каждый образ имеет хотя бы один прообраз).
Отображение f также является сюрьективным, т.к. для каждого уÎпр2f, имеется хотя бы один хÎпр1f такой, что у = f(x).
Так как gодновременно инъективно и сюрьективно, то оно является биективным отображением.
fнеявляется биективным отображением.
Найдем композицию отображений:
(f∘g)(x) = f(g(x)) =–(g(x)+1)2 =–(–x–2+1)2= –(–x–1)2=–(x+1)2,
(g∘f)(x) = g(f(x)) =–f(x)–2 = –(–(x+1)2) –2 =(x+1)2–2.
Отображение f обратимо справа, как сюрьекция. И 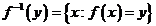, где y≤ 0. Из выражения y=–(x+1)2 найдем x.
Тогда 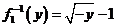и 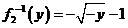, где y≤ 0.
При этом, (f∘f ‑1)(у)= f(f ‑1(y))= 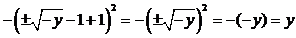– тождественное отображение при y ≤ 0.
Отображение g обратимо как слева, так и справа, как биекция. И 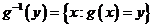, где y любое. Из выражения 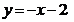следует: 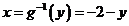. И при этом: (g∘g‑1 )(у) = g(g‑1(y)) = –(–2–y)–2 = y
и(g‑1∘g )(х) =g‑1(g(х)) = –2–(–x-2) = x – тождественные отображения.
Посвойствам композиции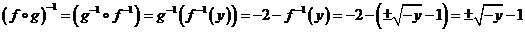
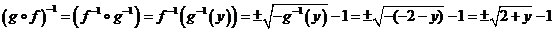
f(A) = {y = f(x), гдеxÎA }, поэтомуf(A)=[–4; –0,25].
Аналогично, g(A) = {y = g(x), где xÎA } = [–3; –0,5].
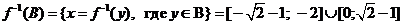
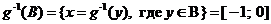
Найдем неподвижные точки. По определению это такиех, что: f(x)=x и g(x)=x. Таким образом, x = –(x+1)2. Отсюда x2+3x+1=0 и т. к. дискриминант D=9–4=5>0, то 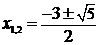– две неподвижные точки f(x).
Из g(x)=x следует, что x=–x–2 и x= –1 – неподвижная точка g(x).
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах:
x → (y ↓ z) = (x → y ) ↓ (x → z)
((x ≡ y) · (x | y)) ≡ x&y
Решение:
1. Составим таблицы истинности для функций
| x | y | z | (y ↓ z) | x → (y ↓ z) |
| x | y | z | (x → y ) | (x → z) | (x → y ) ↓ (x → z) |
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функции
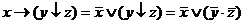
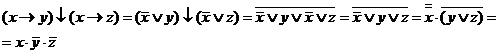
Так как полученные выражения не равны, то функции не эквивалентны.
2. Составим таблицы истинности для функций
| x | y | x&y |
| x | y | x ≡ y | x | y | (x ≡ y) · (x | y) |
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функцию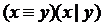
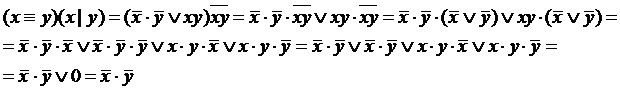
Так как выражения 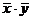и 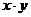не равны, то функции не эквивалентны.
Задача 4.Определить к каким классам относится функция следующего вида: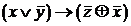
Решение:
| x | y | z | | | |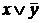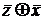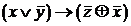
f(0,0,0) = 0 => функция принадлежит к классу Т0– классуфункций, сохраняющих 0,
f(1,1,1) ≠ 1=> функция не принадлежит кклассу Т1 – классу функций, сохраняющих 1,
f(0,0,0) ≠ 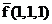=> функция не принадлежит к классуS– классу самодвойственных функций,
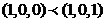, а 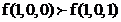=> функция не принадлежит к классу M – классу монотонных функций.
Составим для функции полином Жегалкина (методом неопределенных коэффициентов):
f=c0Åc1xÅc2yÅc3zÅc12xyÅc13xzÅc23yzÅc123xyz
f(0,0,0)= c0=0
f(0,0,1)= c0Åc3=1® c3=1
f(0,1,0)= c0Åc2=1® c2=1
f(0,1,1)= c0Åc2Åc3Åc23=1® c23=1
f(1,0,0)= c0Åc1=1® c1=1
f(1,0,1)= c0Åc1Åc3Åc13=0® c13=0
f(1,1,0)= c0Åc1Åc2Åc12=1® c12=1
f(1,1,1)= c0Åc1Åc2Åc3Åc12Åc13Åc23Åc123=0® c123=1
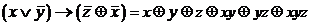
функция является линейной, если ее полином Жегалкина имеет вид:
f(x1,x2,…xn)=c0Åc1x1Åc2x2Å…Åcnxn
В нашем случае функция не приводится к такому виду => она не линейна и
не принадлежит к L– классу линейных функций.
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ, принимающей значения 1 на следующих наборах:
0, 1,2,6,8,12,13,14
Решение.
Составим таблицу истинности для функции. В столбце СДНФ показаны элементарные конъюнкции, в строках, где функция принимает единичные значения, а в столбце СКНФ - элементарные дизъюнкции в строках, где функция равна нулю.
| x1 | x2 | x3 | x4 | f | СДНФ | СКНФ |
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| | ||||||
| |
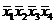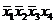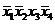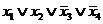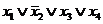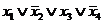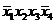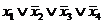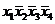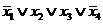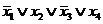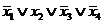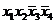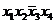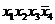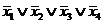Тем самым, совершенная дизъюнктивная нормальная форма (СДНФ):
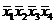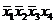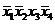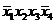f(x)= Ú 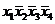Ú Ú 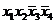Ú Ú 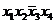Ú Ú .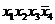
Совершенная конъюнктивная нормальная форма (СКНФ):
f(x)=( )&( )&( )&( )&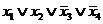
&( )&( )&( )&( )
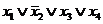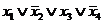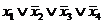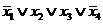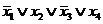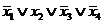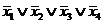Задача 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах: 1,3,5,7,11,12.
Решение:
| Таблица 1 | |||||
| x1 | x2 | x3 | x4 | f | Минтермы |
| | |||||
 | |||||
 | |||||
 | |||||
 | |||||
| | |||||
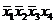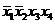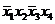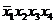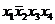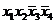1. Составляем таблицу 1 истинности, по которой записываются все минтермы.
2.
Составляем таблицу 2.
| Таблица 2 | ||
| Термы 4 ранга | Термы 3 ранга | Термы 2 ранга |
| * |  * |  |
| * |  * | |
| * |  * | |
| * |  | |
| * |  * | |
| |
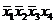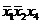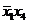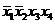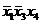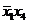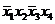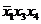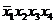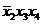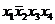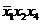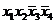Склеиваются импликанты последовательно: 1-2,1-3,1-4,1-5, 1-6. Возможным оказалось склеивание импликант1-2,1-3, около них поставим метку, получились две импликантытретьего ранга, которые записываются во вторую колонку таблицы 2. И так далее до тех пор, пока не будут невозможны дальнейшие склеивания. Получили три импликанты: , ,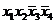
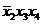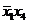
3. Составляется таблица 3 минимального покрытия. Если минтерм содержит первичныйимпликант, то на пересечении соответствующих им строк и столбцов ставится метка.
| Первичные импликаты | Исходные минтермы | |
| | | <
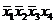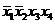