Интеграл. Определенный интеграл. Свойства.

Неопределенным интегралом от функции f(x), определенной на интервале (a;b) называют совокупность F(x) +C всех первообразных функции f(x), определенных не интервале (a;b) и обозначают ʃ f(x)dx = F(x) + C, где f(x) – подынтегральная функция, f(x)dx – подынтегральная выражение, х – переменная интегрирования, С – произвольная постоянная.

Приращение F(b) – F(a) любой из первообразных функций F(x) + C при изменении аргумента от x = a до x = b называется определенным интегралом от a до b функции f(x) и обозначается 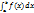, где a и b – пределы интегрирования (a – нижний, b – верхний), [a;b] – отрезок интегрирования, f(x) – подынтегральная функция, x – переменная интегрирования.

Основные свойства определенного интеграла:

1⁰. Определенный интеграл с одинаковыми пределами равен 0: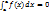

2⁰. При перестановке пределов интегрирования знак интеграл меняется на противоположный: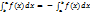

3⁰. Отрезок интегрирования можно разбить на части: 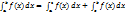, где a < c < b.

4⁰. Постоянный множитель можно выносить за знак интеграла: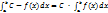

5⁰. Интеграл от алгебраический суммы функции равен алгебраической сумме интегралов от всех слагаемых: .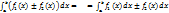

6⁰. Оценка определенного интеграла: если m ≤ f(x) ≤ M на [a; b], то m(b-a)M < 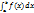< M(b-a).

Чтобы вычислить определенный интеграл, нужно:

Найти неопределенный интеграл от функции f(x), в котором можно принять C = 0;

В полученном выражении вместо аргумента х подставить сначала верхний предел b, а затем нижний предел a;

Из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.

3.Вычислить интеграл: .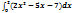

Билет № 18

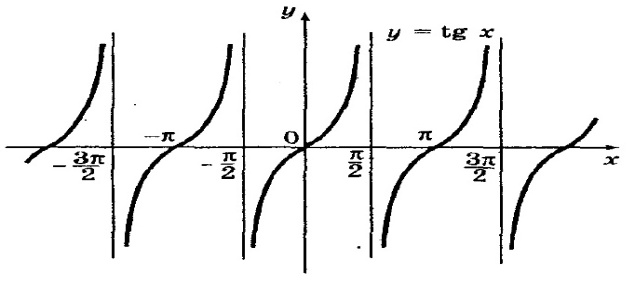
1.Функция y=tg(x) ее свойства и график.

Область определения 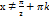, где k принадлежит к множеству целых чисел.

Область значений – вся числовая прямая.

Функция периодична с основным периодом π.

Функция нечетная.

Функция возрастает на промежутках .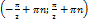

2.Интеграл. Неопределенный интеграл. Свойства.

Неопределенным интегралом от функции f(x), определенной на интервале (a;b) называют совокупность F(x) +C всех первообразных функции f(x), определенных не интервале (a;b) и обозначают ʃ f(x)dx = F(x) + C, где f(x) – подынтегральная функция, f(x)dx – подынтегральная выражение, х – переменная интегрирования, С – произвольная постоянная.

Основные свойства неопределенного интеграла:

1⁰. Производная неопределенного интеграла равна подынтегральной функции .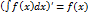

2⁰. Дифференциал неопределенного интеграла равен подынтегральному выражению: d =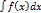

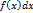
3⁰. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная: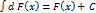

4⁰. Постоянный множитель можно выносить за знак интеграла: 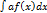= a 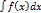, где а – постоянная, а ≠ 0.

5⁰. Неопределенный интеграл от алгебраической суммы непрерывных функций равен алгебраической сумме интегралов от каждой функции: =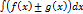

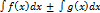
3. Найти неопределенный интеграл а) .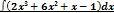

Билет № 19

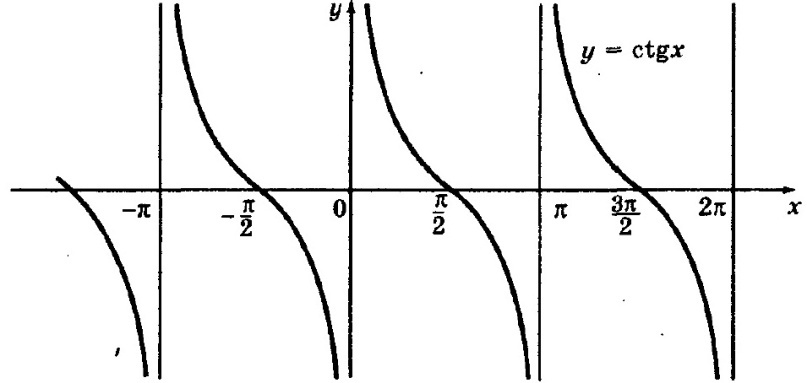
1.Функция y=ctg(x), ее свойства и график.

Область определения 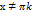, где k принадлежит к множеству целых чисел.

Область значений – вся числовая прямая.

Функция периодична с основным периодом π.

Функция нечетная.

Функция возрастает на промежутках 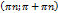.