Исследование СЛАУ(Теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)

Ранг м-цы.

Рассм. м. А раз-ти m×n, т.е. м. 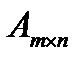. Выберем в ней произв. образом s-разл. строк и s-разл. столбцов , при 1<S≤min(m;n). Эл-ты стоящ. на прерсеч. выбр. строк и столбцов образует м. пор. s. Опр-ль этой м. наз. минором пор. s м-цы А. Нек. миноры могут быть =0. Рангом м. наз. наиб. из порядков её миноров отлич. от 0. Ранг м.: r, rang A, rank A. Если все миноры м. =0, то её ранг =0. Из опред-я ранга м. плуч. след. св-ва: 1.Р.м. удовл. нер-ву 0≤r≤min(m;n);2.Р.м.=0, тогда, когда м. нулевая;3.Для кв. м.n-го п-ка r=n, тогда, когда м. явл. невырожденной. Замеч.: при нахожд. ранга м. с помощью элем-х преобраз. над м. дпеанную м. приводят к трапецеидальному виду.

СЛУ. Осн. понятия.

Системой m лин.ур-ий с n неизв. 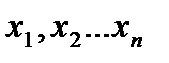наз. системой вида:

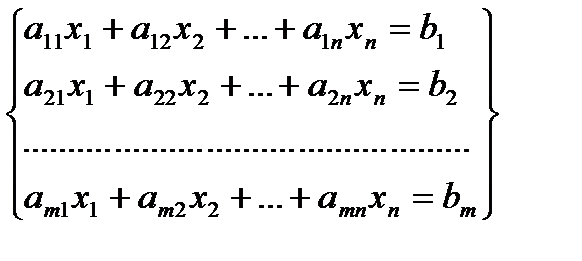
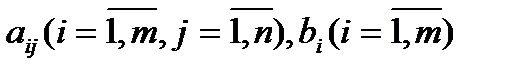
Где числа 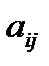наз. коэфф. систем, числа 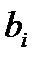-своб. членами системы.

Сист., имеющая хотя бы одно реш-е, наз. совместной, а не имеющая ни одного – несовместной.

Заметим, что однородна сист. Всегда совместна, т.к. она имеет нулевое решение.

Совместная система наз. опред-ой если имеет единственное решение, и наоборот – неопред-ой.

Две системы наз. эквивал-ми или равносильными, если всякое решение одной из них является решением другой.

Элементарные преобраз-ми ЛСУ наз. след.: 1.Умнож. урав-я системы на число отличн. от 0. 2.Прибав-е к одному др. его ур-е умнож-го на число. 3. Перестановка местами 2-х ур-й системы. 4. Вычёркивание ур-я состоящего из нулей.

Линейную с.1 можно написать в матричном виде:

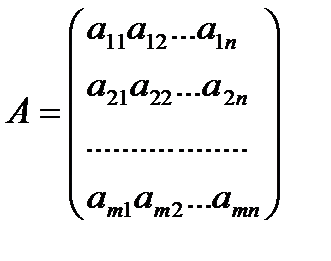
Составленная из коэф. системы 1 наз. матрицей системы, а матрица

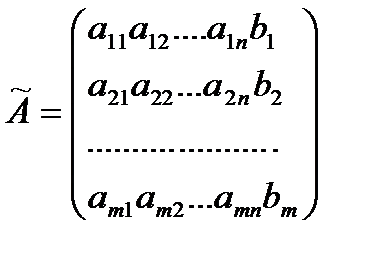- расширенная матрица системы

Рассмотрим матрицы – столбцы составленные из неизвестных и свободных членов.

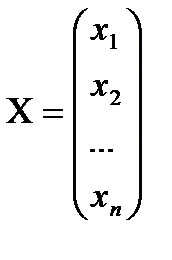
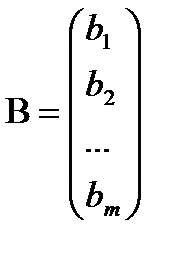
Поскольку м. 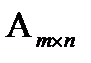согласованна с м. 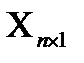, то можно найти произведение

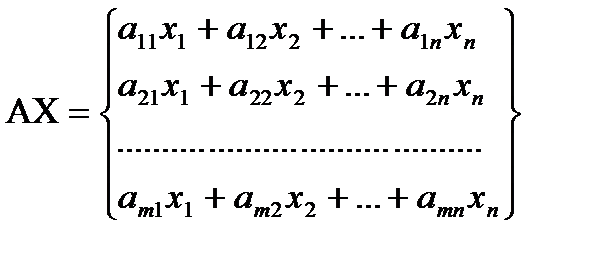
Поэтому сист. 1 можно записать в матричной форме: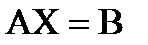

Если 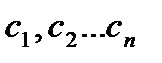решение системы 1, то

матрица 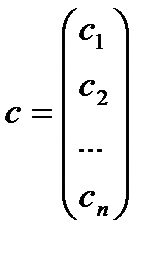наз. векторос решений системы 1.

Выражение «решить систему» означает выяснить совместна она или нет. И в случае совместности найти её решения.

22. Решение СЛУ с помощью определителей (теорема Крамера)

Рассм. систему n лин. ур-й с n неизв. Эта система наз. невыраженной, если определитель м.с. ≠0 (det A≠0).

∆= det A

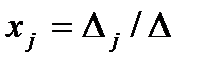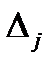Теорема Крамера: если опред. матричной системы n лин. ур-й с n неизв. ≠0, то слу имеет единственное решение, кот. Можно найти по формуле , где - определитель полученный из определителя матричной системы заменой j-го столбца столбцом свободных членов,∆ -определитель системы.

Матричный метод реш. СЛАУ

Пусть дана система из трех уравнений с темя нейзв.:

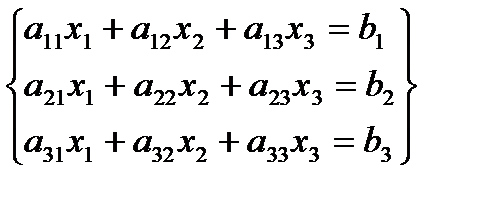
Рассмотрим матрицу системы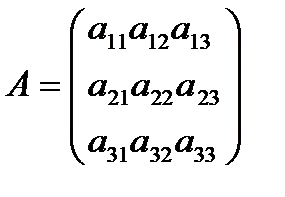

И матрицы столбцы неизвестных и свободных членов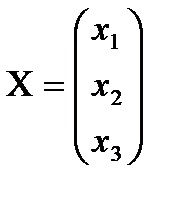

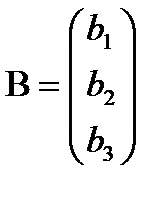
Найдем произведение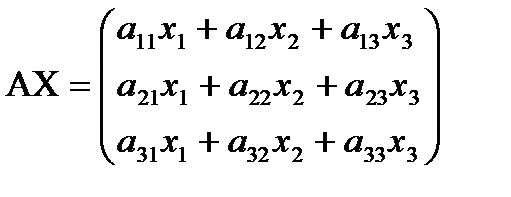

Тогда получаем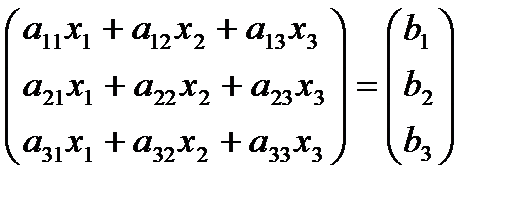

Или короче А*Х=В.

Здесь матрицы А и В известны, а матрица Х неизвестна. Её нужно найти, т.к. её элементы являются решением данной системы. Это уравнение наз. матричным уравнением.

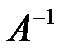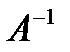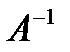Пусть определитель матрицы отличен от нуля det A≠0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу , обратную матрице А: (АХ)= В. Поскольку 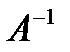А=У и У*Х=Х, то получаем решение матричного уравнения в виде Х= 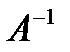В.

Заметим, что поскольку обратную матрицу можно найти только для квадр. матриц, то матричный метод можно решать только те системы, в которых число ур-й совпадает с числом неизв. Однако матричная запись системы возможна и в случае, когда число ур-й не равно числу неизв-х, тогда матрица А не будет квадратной и поэтому нельзя найти решение системы в виде Х= 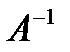В.

Комплексные числа

Исторически понятие КЧ возникло как расширение множества R действит. чисел до такой системы чисел, кот обознач. С и в кот квадратное ур-е 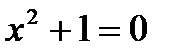имело бы решение.

КЧ наз. число вида 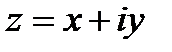, где x и y – действит. числа,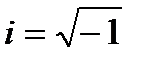

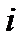- мнимая единица,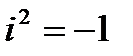

Число х наз. действит. (вещественной) частью КЧ, а y – мнимой. Для этих чисел приняты обозначения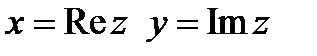

Если y=0, то 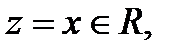если х=0, то 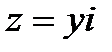наз. числом мнимым.

При это всякому КЧ 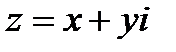соотв. точка y с коорд. плоскостью 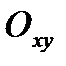. Поэтому плоскость 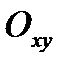наз. комплексной, 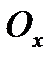- действ. ось, 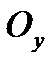- мнимая ось.

Два КЧ 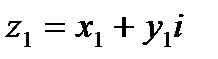и 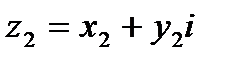равны тогда когда равны их действ. и мнимые части.

КЧ 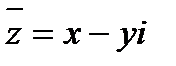наз. комплексосопряженно числу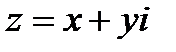

Действия над КЧ:

1.

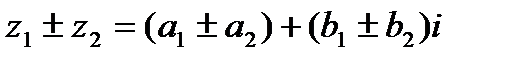
2.

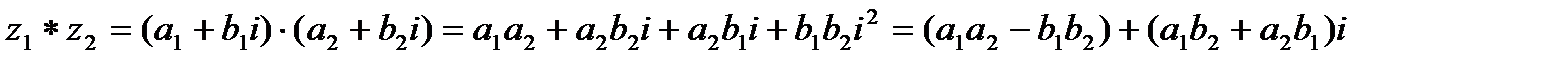
3.

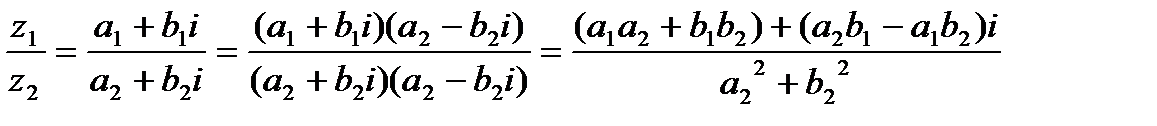
Модулем КЧ 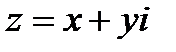наз. длина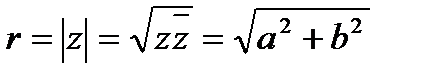

Угол ф между осью абсцисс и вектором ОМ, изображающим комплексное число a+b*I, наз. аргументом КЧ a+b*I.

Понятие вектор. Основные понятия.

Величина, кот. полностью хар-ся своим числовым значением, кот. выражает отношение данной величины к соотв. ед. измерения наз. скалярной величиной или скаляром. Например, в физике m, t, P, V, A. Также физ. величины как сила, скорость, ускорение, перемещение хар-ся не только величиной, но и направлением, наз. вектором.

Вектор представляет собой направленный отрезок. Если его нач. т. А, а кон. – В, то его обозн. .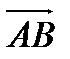

Длинной или модулем вектора 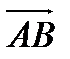наз. длинна отр. .

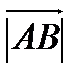Вектор, нач. и конец кот. совпадают, а длина=0, наз. нулевым вектором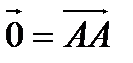

Вектор наз. единичным, если его длина=1. Обозн.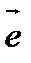

Векторы лежащие на одной или параллельных прямых наз. коллинеарными.

Колл. Векторы могут быть сонаправленными или противоположнонапрвленными.

Един. вектор, направление кот. совпад. с направлением данного вектора а наз. орт вектора а, .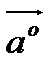

Два вектора наз. равными, если они одинаково направлены и имеют одинаковые длины.

Множество всех векторов = данному вектору 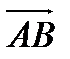наз. свободным вектором и обознач.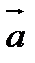

Ранг м-цы.

Рассм. м. А раз-ти m×n, т.е. м. 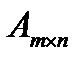. Выберем в ней произв. образом s-разл. строк и s-разл. столбцов , при 1<S≤min(m;n). Эл-ты стоящ. на прерсеч. выбр. строк и столбцов образует м. пор. s. Опр-ль этой м. наз. минором пор. s м-цы А. Нек. миноры могут быть =0. Рангом м. наз. наиб. из порядков её миноров отлич. от 0. Ранг м.: r, rang A, rank A. Если все миноры м. =0, то её ранг =0. Из опред-я ранга м. плуч. след. св-ва: 1.Р.м. удовл. нер-ву 0≤r≤min(m;n);2.Р.м.=0, тогда, когда м. нулевая;3.Для кв. м.n-го п-ка r=n, тогда, когда м. явл. невырожденной. Замеч.: при нахожд. ранга м. с помощью элем-х преобраз. над м. дпеанную м. приводят к трапецеидальному виду.

СЛУ. Осн. понятия.

Системой m лин.ур-ий с n неизв. 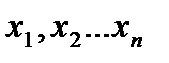наз. системой вида:

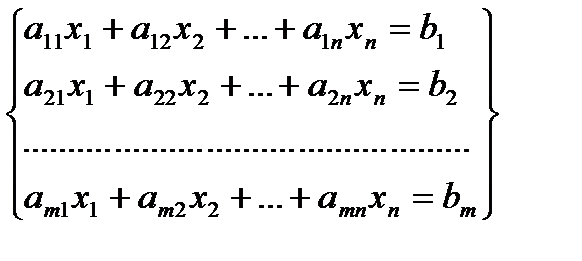
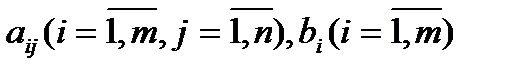
Где числа 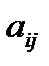наз. коэфф. систем, числа 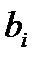-своб. членами системы.

Сист., имеющая хотя бы одно реш-е, наз. совместной, а не имеющая ни одного – несовместной.

Заметим, что однородна сист. Всегда совместна, т.к. она имеет нулевое решение.

Совместная система наз. опред-ой если имеет единственное решение, и наоборот – неопред-ой.

Две системы наз. эквивал-ми или равносильными, если всякое решение одной из них является решением другой.

Элементарные преобраз-ми ЛСУ наз. след.: 1.Умнож. урав-я системы на число отличн. от 0. 2.Прибав-е к одному др. его ур-е умнож-го на число. 3. Перестановка местами 2-х ур-й системы. 4. Вычёркивание ур-я состоящего из нулей.

Линейную с.1 можно написать в матричном виде:

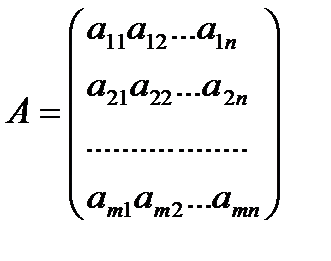
Составленная из коэф. системы 1 наз. матрицей системы, а матрица

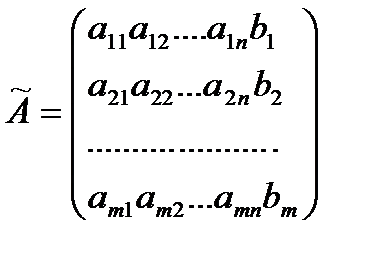- расширенная матрица системы

Рассмотрим матрицы – столбцы составленные из неизвестных и свободных членов.

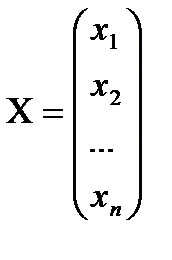
Поскольку м. 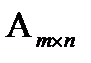согласованна с м. 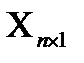, то можно найти произведение

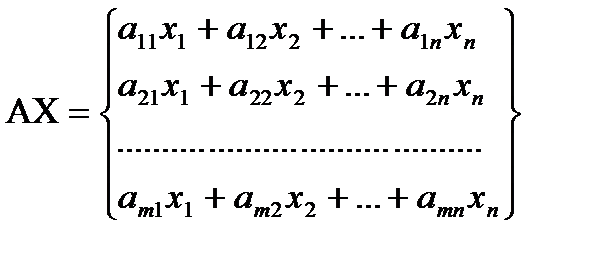
Поэтому сист. 1 можно записать в матричной форме: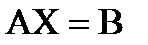

Если 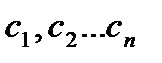решение системы 1, то

матрица наз. векторос решений системы 1.

Выражение «решить систему» означает выяснить совместна она или нет. И в случае совместности найти её решения.

22. Решение СЛУ с помощью определителей (теорема Крамера)

Рассм. систему n лин. ур-й с n неизв. Эта система наз. невыраженной, если определитель м.с. ≠0 (det A≠0).

∆= det A

Теорема Крамера: если опред. матричной системы n лин. ур-й с n неизв. ≠0, то слу имеет единственное решение, кот. Можно найти по формул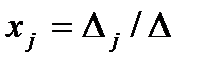е , где 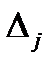- определитель полученный из определителя матричной системы заменой j-го столбца столбцом свободных членов,∆ -определитель системы.

Исследование СЛАУ(Теорема Кронекера-Капелли, базисный минор, базисные и свободные неизвестные)

Теорема Кронекера-Капелли:

1.Рассм. сист. 1, m лин. ур-й с n неизв. Совместна тогда, когда r матр. системы = r расшир. м. c.

2.Если r матр. системы = r расшир. м. с. =n следовательно система имеет единственное решение.

3.Если r матрицы = r расшир. матрицы < n след. система имеет бескон. много решений.

Базисный минор. В матрице порядка m×n минор порядка r называется базисным, если он не равен нулю, а все миноры порядка r+1 и выше равны нулю, или не сущ. вовсе, т.е. r совпадает с меньшим из чисел m или n. Столбцы и строки, на кот. стоит базисный минор, также наз. базисными.

Базисные и свободные неизвестные.

Если ранг системы меньше числа неизвестных и система разрешима, то решений получится множество, это множество решений принято описывать специальным образом. Например, пусть имеется 3 неизвестных, а независимых ур-й только 2. Одно из неизв. можно перенести (вместе с его коэфф.) в правую часть (с обратным знаком), и объяснить это неизвестное «свободным». Ему можно произвольно задать любые значения, а оставшиеся 2 неизвестных будут единственным образом выражаться через правые части. Эти 2 неизв. наз. «базисными».

Пример: x+y+z=2, x-y+z=3; x+y=2-z, x-y=3-z

Здесь z – свободное неизвестное, x,y – базисные неизвестные

Ответ: x=5/2-z, y=1/2

Матричный метод реш. СЛАУ

Пусть дана система из трех уравнений с темя нейзв.:

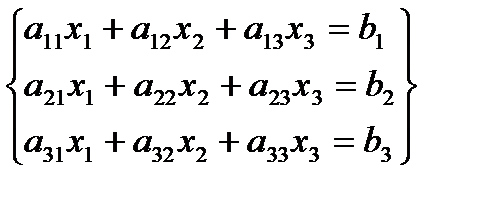
Рассмотрим матрицу системы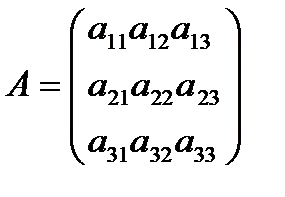

И матрицы столбцы неизвестных и свободных членов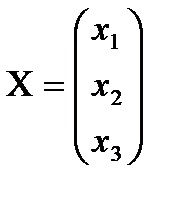

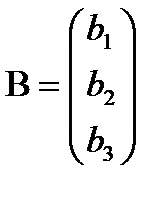
Найдем произведение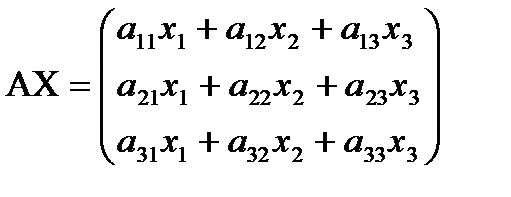

Тогда получаем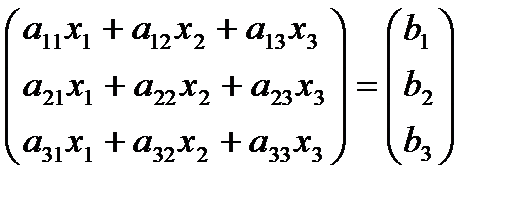

Или короче А*Х=В.

Здесь матрицы А и В известны, а матрица Х неизвестна. Её нужно найти, т.к. её элементы являются решением данной системы. Это уравнение наз. матричным уравнением.

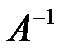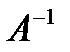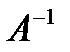Пусть определитель матрицы отличен от нуля det A≠0. Тогда матричное уравнение решается следующим образом. Умножим обе части уравнения слева на матрицу , обратную матрице А: (АХ)= В. Поскольку 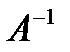А=У и У*Х=Х, то получаем решение матричного уравнения в виде Х= 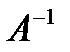В.

Заметим, что поскольку обратную матрицу можно найти только для квадр. матриц, то матричный метод можно решать только те системы, в которых число ур-й совпадает с числом неизв. Однако матричная запись системы возможна и в случае, когда число ур-й не равно числу неизв-х, тогда матрица А не будет квадратной и поэтому нельзя найти решение системы в виде Х= 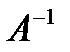В.