Полная схема исследования функции и построения ее графика

Общие исследование функции y = f(x).

• Область определения функции. Найти ее область определения D(f) . Если это не слишком сложно, то полезно найти также область значений E(f) . (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)
• Особые свойства функции.Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox. Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.
• Вертикальные асимптоты.Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения D(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
• Наклонные и горизонтальные асимптоты. Если область определения D(f) вклоючает в себя лучи вида (a;+ 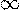)или (− 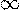;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) пр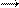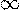и x + или x 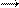− 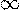соответственно, т.е. найти limx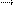 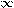f(x). Наклонные асимптоты: y = kx + b, где k=limx 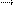+ 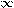xf(x)и b=limx 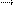+ 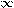(f(x)−x). Горизонтальны асимптоты: y = b, где limx f(x)=b.
• Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.
• Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.

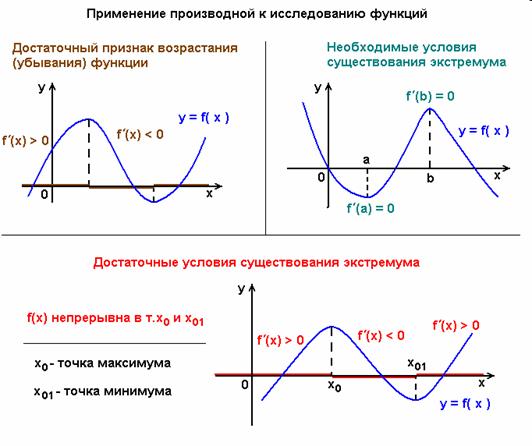
Исследования с помощью производной (продолжение)

Интегральное исчесление:

9- Неопределённый интегра́л для функции 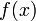— это совокупность всех первообразных данной функции.

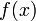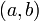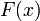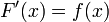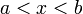Если функция определена и непрерывна на промежутке и — её первообразная, то есть при , то

,

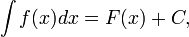
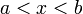где С — произвольная постоянная.

Свойства:

1)постоянную можно выносить за знак интеграла.

2)интеграл суммы равен сумме интегралов.

3)производная от интеграла равна подынтегральной функции.

4)интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.

Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, прилегающей к оси Ox и ограниченной кривой у=f(x)

и прямыми у=0; х=а; х=b.

10-Неопределённый интегра́л для функции 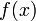— это совокупность всех первообразных данной функции.

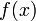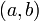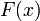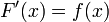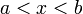Если функция определена и непрерывна на промежутке и — её первообразная, то есть при , то

,

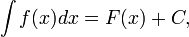
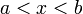где С — произвольная постоянная.

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

11-Неопределённый интегра́л для функции 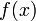— это совокупность всех первообразных данной функции.

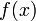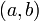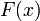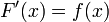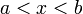Если функция определена и непрерывна на промежутке и — её первообразная, то есть при , то

,

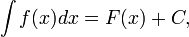
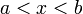где С — произвольная постоянная.