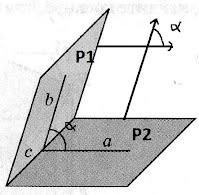
Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей.
1) Угол между плоскостями. Один из смежных углов между плоскостями равен углу между их смежными векторами. ПУСТЬ P1:A1x+B1y+C1z+D1=0; и ; P2:A2x+B2y+C2z+d2=0; n1(A1;B1;C1) и n2(A2;b2;c2); 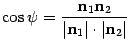 => => 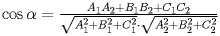 . угол между плоскостями 2) Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, . угол между плоскостями 2) Условия перпендикулярности 2х плоскостей. Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, 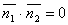 или или 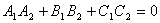 . Таким образом, . Таким образом, 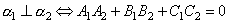 . 3) Условия параллельности 2х плоскостей.Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы . 3) Условия параллельности 2х плоскостей.Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы 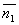 и и 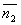 параллельны, а значит параллельны, а значит 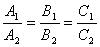 |
17.Уравнение плоскости, заданной тремя точками
Любые ли три точки пространства задают плоскость? Нет. Во-первых, точки должны быть различными. А во-вторых, они не должны лежать на одной прямой (сразу все три).
Уравнение плоскости, проходящей через три различные точки 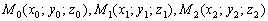 , которые не лежат на одной прямой, можно составить по формуле:
, которые не лежат на одной прямой, можно составить по формуле:
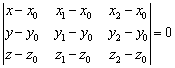
На самом деле это разновидность предыдущего способа, смотрим на картинку:
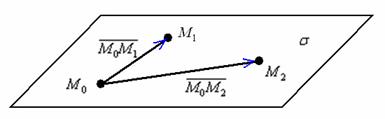
Если известны три различные точки, не лежащие на одной прямой, то легко найти два неколлинеарных вектора, параллельных данной плоскости:
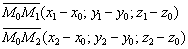
То есть, наша формула фактически совпадает с формулой предыдущего параграфа. Многие уже заметили явную аналогию с материалами статьи Уравнение прямой на плоскости. Закономерности будут сохраняться и дальше!
Чтобы не умереть от скуки, предлагаю раскрутить примеры-шарады:
Пример 3
Составить уравнение плоскости по точкам 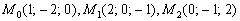 .Решение: составим уравнение плоскости по трём точкам. Используем формулу:
.Решение: составим уравнение плоскости по трём точкам. Используем формулу:
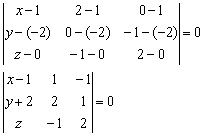
Вот теперь и аналитически видно, что всё дело свелось к координатам двух векторов. Раскрываем определитель по первому столбцу, находим уравнение плоскости:
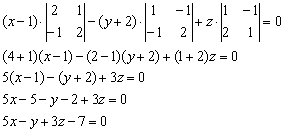
Больше ничего упростить нельзя, записываем:
Ответ: 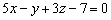
18.Уравнение плоскости, заданной точкой и двумя параллельными векторами
Рассмотрим точку 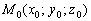 и два неколлинеарных вектора
и два неколлинеарных вектора 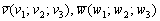 .Уравнение плоскости, которая проходит через точку
.Уравнение плоскости, которая проходит через точку 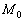 параллельно векторам
параллельно векторам 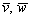 ,выражается формулой:
,выражается формулой:
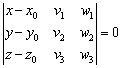
! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости. Для наглядности я буду откладывать векторы прямо в плоскости.
Принципиально ситуация выглядит так:
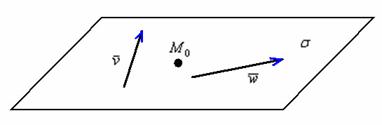
Обратите внимание, что точка и два коллинеарных вектора не определят плоскость (векторы будут свободно «вертеться» вокруг точки).
Пример 1
Составить уравнение плоскости по точке 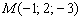 и векторам
и векторам 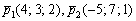 .
.
Решение: Составим уравнение плоскости по точке и двум неколлинеарным векторам:
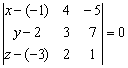
Определитель удобнее всего раскрыть по первому столбцу:
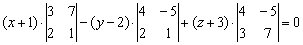
Раскрываем определители второго порядка:
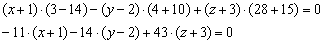
На первом месте у нас находится знак «минус». Хорошим тоном считается убрать наглеца, в этих целях меняем знак у каждого слагаемого. Проводим дальнейшие упрощения и получаем уравнение плоскости:
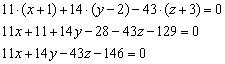
Сократить здесь ничего нельзя, поэтому:
Ответ: 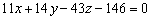
19. Уравнение прямой (в пространстве), заданной двумя точками. Каноническое уравнение прямой в пространстве.
