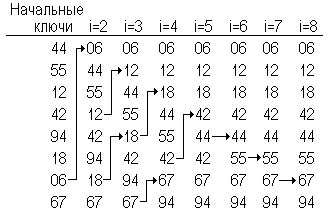
Словесное описание алгоритма

0. В готовую подпоследовательность записывается a₁, во входную – a₂,…,a_{n .}

1. i:=2.

2. Переносим элемент х=a_i из входной подпоследовательности в готовую так, чтобы последняя осталась подсортированной. Для этого:

а) организуем бинарный поиск места включения х в готовую подпоследовательность: находим срединный элемент готовой подпоследовательности - a_m, где m = ]i/2[, и сравнивая его с х. Если a_m>х, то ведём далее поиск в левой половине готовой подпоследовательности, т.е. опять находим срединный элемент и сравниваем его с х, и т.д. пока не найдём номер j такой, что a_j≤x<a_j+1; иначе аналогично ведём поиск в правой половине готовой подпоследовательности;

б) если j=j-1, то переходим к п. в), иначе расширяем готовую подпоследовательность справа, сдвигая её элементы, начиная с a_j+1, вправо.

в) a_j+1:=x.

3. i:=i+1. Если i≤n, то переходим на п. 2, иначе сортировка закончена.

1.3. Сортировка простым выбором

Этот метод основан на следующем правиле:

1. Выбирается во входной подпоследовательности элемент с наименьшим ключом.

2. Он меняется местами с первым элементом a₁.

Эти операции затем повторяются с оставшимися n-1 элементами, затем с n-2элементами, пока не останется только один элемент – наибольший. Этот метод продемонстрирован на тех же восьми ключах в табл. 1.2 (подчеркнуты элементы, которые не изменили своего места).

Таблица 1.2

Этот метод сортировки, называемый простым выбором, в некотором смысле противоположен методу простых включений; при сортировке простыми включениями на каждом шаге рассматривается только один очередной элемент входной подпоследовательности и все элементы готового массива для нахождения места включения; при сортировке простым выбором рассматриваются все элементы входного массива для нахождения элемента с наименьшим ключом, и этот один очередной элемент отправляется в готовую подпоследовательность.

Словесное описание алгоритма.

1. i:=1

2. k присваиваем индекс наименьшего элемента подпоследовательности a_i,…,a_n.

3. Если i≠k, то a_i и a_k обмениваем местами.

4. I:=i+1. Если i< n, то переходим на п. 2, иначе сортировка закончена.

1.4. Сортировка простым обменом

Классификация методов сортировки не всегда чётко определена. Оба представленных ранее метода можно рассматривать как сортировку обменом. Однако в этом разделе мы остановимся на методе, в котором обмен двух элементов является основной характеристикой процесса.

Приведенный ниже алгоритм сортировки простым обменом основан на принципе сравнения и обмена пары соседних элементов до тех пор, пока не будут рассортированы все элементы. Как и в предыдущем методе простого выбора, совершаем повторные проходы по массиву, каждый раз просеивая наименьший элемент оставшегося множества, двигаясь к левому концу массива. Для разнообразия будем рассматривать массив, расположенный вертикально, а не горизонтально, и представим себе элементы пузырьками в резервуаре с водой, обладающими "весами", которые соответствуют их ключам. Тогда каждый проход по массиву приводит к "всплыванию" пузырька на соответствующий его весу уровень (табл. 1.3). Полуофициальное название этого метода - метод пузырька.

Таблица 1.3

Словесное описание алгоритма

1. I:=2.

2. Просматриваем каждую пару рядом стоящих элементов a_i,…,a_n, начиная от конца (от n к i). Если элемент с меньшим ключом больше элемента с большим ключом (a_j<a_j-1), то обмениваем их местами.

3. I:=i +1. Если i ≤n, то переходим на п. 2, иначе сортировка окончена.

Этот алгоритм легко оптимизировать. Пример в табл. 1.3 показывает, что три последних прохода никак не влияют на порядок элементов, поскольку те уже рассортированы. Очевидный способ улучшить данный алгоритм – это запоминать, производился ли на данном проходе какой-либо обмен. Если нет, то это означает, что алгоритм закончил работу. Этот процесс улучшения можно продолжить, если запоминать не только сам факт обмена, но и место (индекс k) последнего обмена (все пары соседних элементов с индексами, меньшими k, уже расположены в нужном порядке). Поэтому следующие проходы можно заканчивать на этом индексе, вместо того чтобы двигаться до установленной заранее нижней границы i.

Внимательный программист заметит здесь странную асимметрию: один неправильно расположенный "пузырек" в "тяжелом" конце массива всплывёт на место за один проход, а неправильно расположенный элемент в "легком" конце будет опускаться на правильное место только на один шаг на каждом проходе. Например, массив 12 18 42 44 55 67 94 06 будет рассортирован при помощи метода пузырька за один проход, а сортировка массива 94 06 12 18 42 44 55 67 потребует семи проходов. Эта асимметрия подсказывает третье улучшение: менять направление следующих один за другим проходов. Тогда будет иметь место чередование "всплытий пузырьков" и "падений камней". Полученный в результате улучшенный алгоритм называется шейкер-сортировкой. Его работа показана в табл. 1.4 на тех же восьми ключах, которые использовались в предыдущих таблицах; текущий массив ограничен слева и справа (параметры l и r ).