Извлечение квадратного корня

Извлечение квадратного корня из комплексного числа можно осуществить, не обращаясь к тригонометрической форме. Выведем алгебраическую формулу для выполнения этого действия.

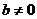Пусть , и положим ,так как только этот случай представляет интерес. Тогда , что равносильно системе уравнений и , причем нас интересуют только действительные решения этой системы. Мы уже знаем, что задача имеет решения. Это дает право предположить, что под буквами х и у подразумевается решение задачи. Тогда , .

Складываем эти равенства, получим: , откуда ,

причем здесь берется арифметическое значение корня, т.к. .

Сопоставляя последнее равенство с первым уравнением системы, получим:

, .

Правые части обоих равенств неотрицательны, т.к. . Из последних равенств находим : , . Т.к. , то , где - обозначает знак b, т.е. +1, если b > 0 и –1, если b < 0.

Пример:

1)

2) .

Корни из единицы

Как и для всякого отличного от нуля комплексного числа, для 1 существует ровно n значений корня n –ой степени. Т.к. 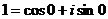, то для корней n – ой степени из 1 имеет место формула:

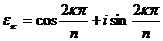, при .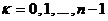

Все корни из 1 имеют модуль, равный 1, так что их изображения находятся на окружности радиуса 1 с центром в точке 0. Один из корней при 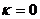есть просто число 1 и изображается точкой пересечения положительной полуоси действительной оси с единичной окружностью. Корень 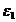имеет аргумент 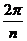, т.е. часть полной окружности.

У

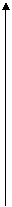1

1 Х

Все корни n – ой степени из 1 являются корнями уравнения 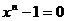и располагаются на единичной окружности, деля ее на n равных частей. По этой причине уравнение 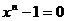носит название уравнения деления круга.

Определение 1: 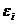называется первообразным корнемn– ой степени из 1, если 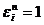, но при любом другом натуральном m < n, 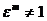. Число 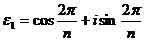, есть, очевидно, первообразный корень n – ой степени из 1, но при n > 2 существуют и другие первообразные корни.

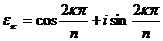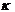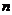Теорема 1:Число есть первообразный корень n – ой степени из 1 в том и только том случая, если и взаимно просты.

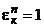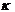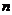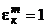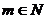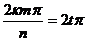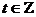Доказательство: Действительно всегда. Пусть и - взаимно просты и пусть , где . Тогда , при и 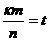, т.е. 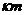- делится на n. Но т.к. 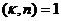, то 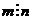и потому не может быть меньше n. Поэтому 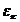есть первообразный корень n – ой степени из 1.

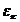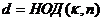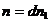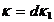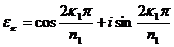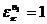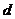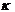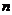Предположим теперь, что есть первообразный корень n – ой степени из 1, и пусть , , . Тогда и . Отсюда следует, что = 1, т.е. и взаимно просты, иначе 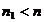и 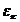- не первообразный корень.

Из доказанной теоремы следует, что число первообразных n – ой степени из 1 равно числу меньших n и взаимно простых с n чисел, т.е. оно равно значению 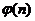функции Эйлера от числа n.

Пример: при n = 12 имеется 4 первообразных корня .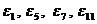

Свойство корней из 1

Предложение 1:Произведение двух корней степени n из 1 есть корень степени n из 1.

Доказательство: Пусть 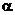и 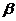корни степени из 1, т.е. 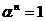и 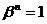. Но тогда 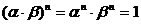т.е. 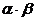- корень n – ой степени из 1.

Предложение 2: Число, обратное корню степени n из 1, есть корень степени n из 1.

Доказательство: Если 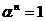, то .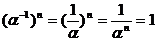

Предложение 3:Пусть 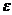- любой первообразный корень степени n из 1. Тогда всякий корень степени n из 1 получается из 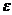возведением в некоторую степень с натуральным показателем.

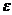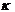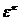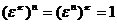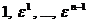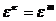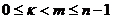Доказательство: Пусть -какой-либо первообразный корень степени n из 1. Тогда при любом целом число будет корнем степени n из 1, ибо . Рассмотрим числа . Все они суть корни степени n из 1. Среди них нет равных, ибо если , при , то 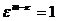, что невозможно, ибо 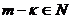, но меньше n, а 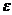- первообразный корень степени n. Итак, числа

(*)

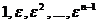
попарно различные корни n-ой степени из 1 и их число равно n, т.е. равно числу всех корней n-ой степени из 1. Поэтому (*) – все корни степени n из 1, что и требовалось доказать.

Предложение 4:Все значения 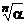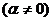получаются из одного значения посредством умножения на все корни степени n из 1.

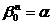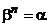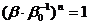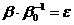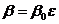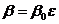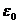Доказательство: Пусть и . Тогда , так, что есть корень n–ой степени из 1 и . Обратно, если и - корень степени n из 1, то .

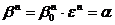Теорема 1. ( Здесь доказано ) Все корни n-ой степени из 1 образуют мультипликативную группу из n элементов.

Теорема 2.Все корни из 1 образуют мультипликативную группу.

( Доказать самостоятельно ).

Первую группу обычно обозначают 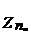,а вторую

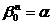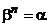Доказательство: Пусть и . Тогда 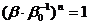, так, что 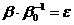есть корень n–ой степени из 1 и 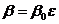. Обратно, есл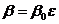и и 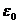- корень степени n из 1, то .

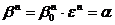Теорема 1. ( Здесь доказано ) Все корни n-ой степени из 1 образуют мультипликативную группу из n элементов.

Теорема 2.Все корни из 1 образуют мультипликативную группу.

( Доказать самостоятельно ).

Первую группу обычно обозначают 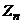,а вторую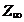

Глава V. Арифметическое векторное пространство и системы линейных уравнений