Понятие сопряженных комплексных чисел
Глава IV. Комплексные числа
Система комплексных чисел
На протяжении курса элементарной алгебры несколько раз происходит обогащение запаса чисел. Школьник, приступающий к изучению алгебры, приносит из арифметики знакомство с натуральными числами, т.е. положительными целыми числами (N). Алгебра начинается по существу с введения отрицательных чисел, т. е. с оформления первой среди важнейших числовых систем – системы целых чисел (Z), состоящей из всех положительных и всех отрицательных целых чисел и нуля, и более широкой системы рациональных чисел (Q), состоящей из всех целых чисел и всех дробных чисел, как положительных, так и отрицательных.
Дальнейшее расширение запаса чисел происходит тогда, когда в рассмотрение включаются иррациональные числа ( 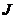 ). Система, состоящая из всех рациональных и иррациональных чисел, называется системой действительных ( или вещественных ) чисел ( R ). Строгое построение системы действительных чисел будет рассмотрено в других разделах математики. Однако сейчас будет достаточно того знакомства с действительными числами, какими обладают выпускники средней школы.
). Система, состоящая из всех рациональных и иррациональных чисел, называется системой действительных ( или вещественных ) чисел ( R ). Строгое построение системы действительных чисел будет рассмотрено в других разделах математики. Однако сейчас будет достаточно того знакомства с действительными числами, какими обладают выпускники средней школы.
Расширение системы действительных чисел до системы комплексных чисел ( С )связано со следующей задачей. Известно, что действительных чисел недостаточно для того, чтобы решить любое квадратное уравнение с действительными коэффициентами. Простейшее из квадратных уравнений, не имеющих корней среди действительных чисел, есть
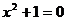 (1);
(1);
только это уравнение будет нас сейчас интересовать. Задача, состоящая перед нами, такова: нужно расширить систему действительных чисел до такой системы чисел, в которой уравнение (1) уже обладало бы корнем.
Комплексными числами называются выражения вида 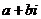 , где
, где 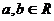 ,
, 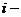 некоторый символ, удовлетворяющий соотношению
некоторый символ, удовлетворяющий соотношению 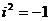 .
.
Задание комплексного числа 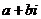 вполне определяется заданием двух обыкновенных вещественных чисел
вполне определяется заданием двух обыкновенных вещественных чисел 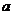 и
и 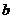 , называемых компонентами.
, называемых компонентами. 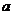 - действительная часть числа, а b - коэффициент мнимой части.
- действительная часть числа, а b - коэффициент мнимой части.
Определим множество комплексных чисел.
Определение 1: Комплексными числами называются упорядоченные пары действительных чисел (компонент), для которых понятия равенства, суммы произведения и отожествления некоторых пар с действительными числами вводятся согласно следующим аксиомам:
I. Пары ( 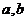 ) и (
) и ( 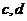 ) считаются равными, т. и т.т. когда равны их соответствующие компоненты; (
) считаются равными, т. и т.т. когда равны их соответствующие компоненты; ( 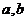 )
) 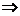 (
( 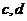 )
) 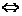
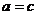 и
и 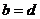 ;
;
II. Суммой пар ( 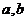 ) и (
) и ( 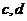 ) называется пара
) называется пара 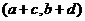 ,т.е.
,т.е. 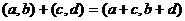 ;
;
III. Произведением пар ( 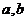 ) и (
) и ( 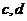 ) называется пара (
) называется пара ( 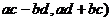 , т.е. (
, т.е. ( 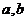 ) (
) ( 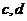 ) = (
) = ( 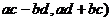 ;
;
IV. Пара ( 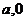 ) отождествляется с действительным числом
) отождествляется с действительным числом 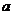 , т.е. (
, т.е. ( 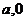 ) =
) = 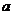 .
.
Проверим, совпадение IV аксиомы и действий, определённых в I – III аксиомах, с действиями над действительными числами.
1. Пусть 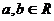 , тогда они отожествляются с (а,0) и (b,0); по аксиоме I
, тогда они отожествляются с (а,0) и (b,0); по аксиоме I 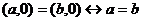 , т.е. сводится к равенству этих чисел в обычном смысле.
, т.е. сводится к равенству этих чисел в обычном смысле.
2. Пусть 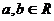 (
( 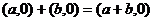 ) или это число
) или это число 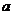 +b, т.е. сумма чисел
+b, т.е. сумма чисел 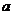 и b в обычном смысле.
и b в обычном смысле.
3. Пусть 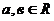 , (а,0) и (b,0) =
, (а,0) и (b,0) = 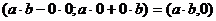 , т.е. равно произведению
, т.е. равно произведению 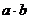 в обычном смысле и аксиома IV согласуется с аксиомами I-III и не приводит к путанице.
в обычном смысле и аксиома IV согласуется с аксиомами I-III и не приводит к путанице.
Обратим внимание на формулу, которая вытекает из аксиом III и IV.
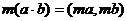 , т.к.
, т.к. 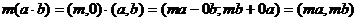 .
.
Свойства действий.
Проверим те свойства операций над комплексными числами, которые будут свидетельствовать о том, что комплексные числа составляют поле. При проверке мы немного переставим аксиомы в ином порядке.
1. Коммутативность сложения : 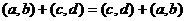 .
.
2.Ассоциативность сложения: 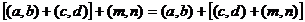 .
.
3. Пара (0,0) играет роль нейтрального элемента относительно сложения:
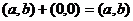 .
.
4. Пара 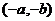 является противоположным элементом для пары
является противоположным элементом для пары 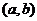 :
:
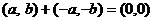 .
.
5. Умножение коммутативно : 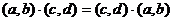 .
.
6. Умножение ассоциативно: 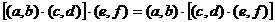 .
.
7. Умножение дистрибутивно относительно сложения:
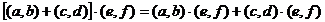 .
.
8. Пара (1,0) является нейтральным элементом относительно умножения:
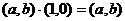 .
.
9. Для любой пары 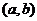 , отличной от нуля существует обратная
, отличной от нуля существует обратная 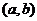 -1:
-1:
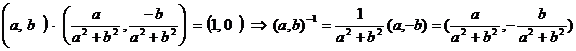 .
.
Доказательство свойств 1, 2 очевидны (точнее, вытекают из соответствующих свойств сложения действительных чисел), т.к. при сложении пар мы отдельно складываем их первые и вторые компоненты пар. Коммутативность умножения основана на том, что в определение произведения пары 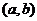 и
и 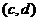 входят симметричным образом.
входят симметричным образом.
Доказательство ассоциативности умножения следует из равенств:
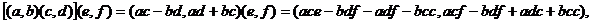
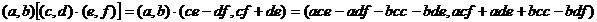
Закон дистрибутивности вытекает из равенств
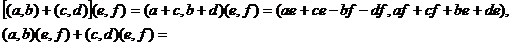
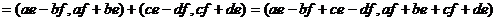
Итак, множество пар является полем. Оно называется полем комплексных чисел.
Геометрическое изображение
Комплексное число 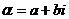 естественно изобразить точкой на плоскости, приняв число
естественно изобразить точкой на плоскости, приняв число 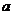 и b за координаты точки, изображающей число
и b за координаты точки, изображающей число 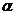 . При этом каждому комплексному числу соответствует точка, и каждой точке плоскости соответствует некоторое комплексное число. Действительные числа изображают точками на оси абсцисс. На оси ординат расположены изображения «чисто мнимых» чисел
. При этом каждому комплексному числу соответствует точка, и каждой точке плоскости соответствует некоторое комплексное число. Действительные числа изображают точками на оси абсцисс. На оси ординат расположены изображения «чисто мнимых» чисел 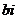 . Началу координат соответствует число 0.
. Началу координат соответствует число 0.
Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексной переменной. Её ось абсцисс называется вещественной осью, ось ординат – мнимой осью.
Наряду с изображением комплексного числа точками на плоскости, удобно с каждым числом связывать вектор, исходящий из начала координат в точку изображающую это число. Поэтому действия сложения комплексных чисел и умножение комплексных чисел на действительное число могут иметь геометрическую интерпретацию.
Корни из единицы
Как и для всякого отличного от нуля комплексного числа, для 1 существует ровно n значений корня n –ой степени. Т.к. 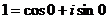 , то для корней n – ой степени из 1 имеет место формула:
, то для корней n – ой степени из 1 имеет место формула:
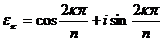 , при
, при 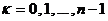 .
.
Все корни из 1 имеют модуль, равный 1, так что их изображения находятся на окружности радиуса 1 с центром в точке 0. Один из корней при 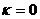 есть просто число 1 и изображается точкой пересечения положительной полуоси действительной оси с единичной окружностью. Корень
есть просто число 1 и изображается точкой пересечения положительной полуоси действительной оси с единичной окружностью. Корень 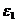 имеет аргумент
имеет аргумент 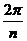 , т.е.
, т.е.  часть полной окружности.
часть полной окружности.
У
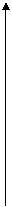 |
 1
1
1 Х

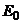
Все корни n – ой степени из 1 являются корнями уравнения 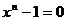 и располагаются на единичной окружности, деля ее на n равных частей. По этой причине уравнение
и располагаются на единичной окружности, деля ее на n равных частей. По этой причине уравнение 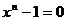 носит название уравнения деления круга.
носит название уравнения деления круга.
Определение 1: 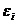 называется первообразным корнемn– ой степени из 1, если
называется первообразным корнемn– ой степени из 1, если 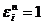 , но при любом другом натуральном m < n,
, но при любом другом натуральном m < n, 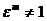 . Число
. Число 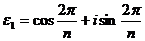 , есть, очевидно, первообразный корень n – ой степени из 1, но при n > 2 существуют и другие первообразные корни.
, есть, очевидно, первообразный корень n – ой степени из 1, но при n > 2 существуют и другие первообразные корни.
Теорема 1:Число 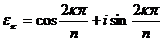 есть первообразный корень n – ой степени из 1 в том и только том случая, если
есть первообразный корень n – ой степени из 1 в том и только том случая, если 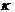 и
и 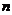 взаимно просты.
взаимно просты.
Доказательство: Действительно 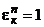 всегда. Пусть
всегда. Пусть 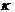 и
и 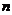 - взаимно просты и пусть
- взаимно просты и пусть 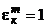 , где
, где 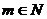 . Тогда
. Тогда 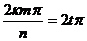 , при
, при 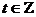 и
и 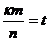 , т.е.
, т.е. 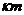 - делится на n. Но т.к.
- делится на n. Но т.к. 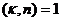 , то
, то 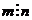 и потому не может быть меньше n. Поэтому
и потому не может быть меньше n. Поэтому 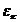 есть первообразный корень n – ой степени из 1.
есть первообразный корень n – ой степени из 1.
Предположим теперь, что 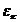 есть первообразный корень n – ой степени из 1, и пусть
есть первообразный корень n – ой степени из 1, и пусть 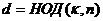 ,
, 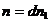 ,
, 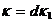 . Тогда
. Тогда 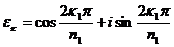 и
и 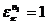 . Отсюда следует, что
. Отсюда следует, что 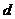 = 1, т.е.
= 1, т.е. 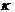 и
и 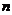 взаимно просты, иначе
взаимно просты, иначе 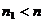 и
и 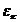 - не первообразный корень.
- не первообразный корень.
Из доказанной теоремы следует, что число первообразных n – ой степени из 1 равно числу меньших n и взаимно простых с n чисел, т.е. оно равно значению 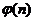 функции Эйлера от числа n.
функции Эйлера от числа n.
Пример: при n = 12 имеется 4 первообразных корня 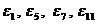 .
.
Свойство корней из 1
Предложение 1:Произведение двух корней степени n из 1 есть корень степени n из 1.
Доказательство: Пусть 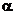 и
и 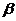 корни степени из 1, т.е.
корни степени из 1, т.е. 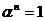 и
и 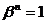 . Но тогда
. Но тогда 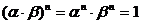 т.е.
т.е. 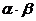 - корень n – ой степени из 1.
- корень n – ой степени из 1.
Предложение 2: Число, обратное корню степени n из 1, есть корень степени n из 1.
Доказательство: Если 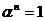 , то
, то 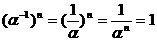 .
.
Предложение 3:Пусть 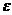 - любой первообразный корень степени n из 1. Тогда всякий корень степени n из 1 получается из
- любой первообразный корень степени n из 1. Тогда всякий корень степени n из 1 получается из 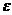 возведением в некоторую степень с натуральным показателем.
возведением в некоторую степень с натуральным показателем.
Доказательство: Пусть 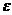 -какой-либо первообразный корень степени n из 1. Тогда при любом целом
-какой-либо первообразный корень степени n из 1. Тогда при любом целом 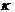 число
число 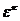 будет корнем степени n из 1, ибо
будет корнем степени n из 1, ибо 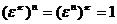 . Рассмотрим числа
. Рассмотрим числа 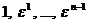 . Все они суть корни степени n из 1. Среди них нет равных, ибо если
. Все они суть корни степени n из 1. Среди них нет равных, ибо если 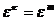 , при
, при 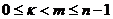 , то
, то 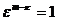 , что невозможно, ибо
, что невозможно, ибо 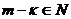 , но меньше n, а
, но меньше n, а 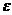 - первообразный корень степени n. Итак, числа
- первообразный корень степени n. Итак, числа
(*) 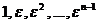
попарно различные корни n-ой степени из 1 и их число равно n, т.е. равно числу всех корней n-ой степени из 1. Поэтому (*) – все корни степени n из 1, что и требовалось доказать.
Предложение 4:Все значения 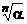
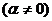 получаются из одного значения посредством умножения на все корни степени n из 1.
получаются из одного значения посредством умножения на все корни степени n из 1.
Доказательство: Пусть 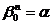 и
и 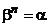 . Тогда
. Тогда 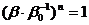 , так, что
, так, что 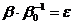 есть корень n–ой степени из 1 и
есть корень n–ой степени из 1 и 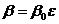 . Обратно, если
. Обратно, если 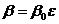 и
и 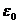 - корень степени n из 1, то
- корень степени n из 1, то 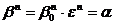 .
.
Теорема 1. ( Здесь доказано ) Все корни n-ой степени из 1 образуют мультипликативную группу из n элементов.
Теорема 2.Все корни из 1 образуют мультипликативную группу.
( Доказать самостоятельно ).
Первую группу обычно обозначают 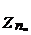 ,а вторую
,а вторую
Доказательство: Пусть 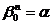 и
и 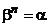 . Тогда
. Тогда 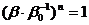 , так, что
, так, что 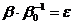 есть корень n–ой степени из 1 и
есть корень n–ой степени из 1 и 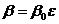 . Обратно, если
. Обратно, если 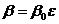 и
и 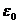 - корень степени n из 1, то
- корень степени n из 1, то 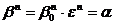 .
.
Теорема 1. ( Здесь доказано ) Все корни n-ой степени из 1 образуют мультипликативную группу из n элементов.
Теорема 2.Все корни из 1 образуют мультипликативную группу.
( Доказать самостоятельно ).
Первую группу обычно обозначают 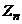 ,а вторую
,а вторую 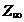
Глава V. Арифметическое векторное пространство и системы линейных уравнений
Система линейных уравнений
Определение 1: Системой линейных уравнений над полем 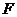 с переменными
с переменными 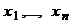 называется система вида
называется система вида
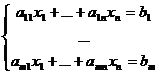 , где
, где 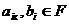 .
.
Эту систему 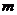 линейных уравнений будем кратко записывать в виде
линейных уравнений будем кратко записывать в виде
(1) 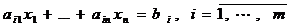 .
.
Допустимыми значениями свободных переменных 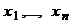 системы линейных уравнений (1) всюду в дальнейшем считаем элементы поля
системы линейных уравнений (1) всюду в дальнейшем считаем элементы поля 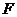 .
.
Определение 2: Вектор 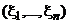 из
из 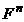 называется решением системы уравнений (1), если верны равенства
называется решением системы уравнений (1), если верны равенства 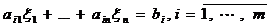 .
.
Определение 3: Система линейных уравнений называется совместной, если она имеет хотя бы одно решение. Системы линейных уравнений называется несовместной, если она не имеет решений.
Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если решений больше, чем одно.
Наряду с системой (1) рассмотрим систему (над 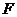 )
)
(2) 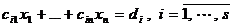 .
.
Отметим, что система линейных уравнений может состоять из одного уравнения.
Определение 4: Система уравнений (2) называется следствием системы уравнений (1), если каждое решение системы (1) является также решением системы (2).
Запись (1) 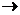 (2) означает, что система (2) есть следствие системы (1).
(2) означает, что система (2) есть следствие системы (1).
Определение 5: Линейное уравнение
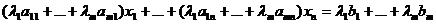 , где
, где 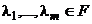 - произвольные числа, называется линейной комбинацией уравнений системы (1) с коэффициентами
- произвольные числа, называется линейной комбинацией уравнений системы (1) с коэффициентами 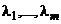 .
.
Предложение 1:Любая линейная комбинация линейных уравнений системы уравнений (1) является следствием этой системы.
Докажите самостоятельно.
Определение 6: Две системы линейных уравнений называются равносильными, если каждое решение любой из этих систем является решением другой системы.
Предложение 2:Две системы линейных уравнений равносильны тогда и только тогда, когда каждая из этих систем является следствием другой системы.
Предложение 3: Две системы линейных уравнений равносильны тогда и только тогда, когда множество всех решений одной системы совпадает с множеством всех решений другой системы.
Определение 7: Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
а) умножение обеих частей какого – нибудь уравнения системы на отличный от нуля скаляр;
б) прибавление (вычитание) к обеим частям какого – либо уравнения системы, соответствующих частей другого уравнения системы, умноженных на скаляр;
в) исключение из системы или присоединение к системе линейного уравнения с нулевыми коэффициентами и нулевым свободным членом: 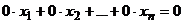 .
.
Теорема 1:Если одна система линейных уравнений получается из другой системы линейных уравнений в результате цепочки элементарных преобразований, то эти две системы равносильны.
Доказательство:Пусть дана система
(1) 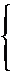
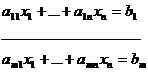 .
.
Если умножить одно из её уравнений, например первое, на отличный от нуля скаляр 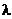 , то получим систему
, то получим систему
(2) 
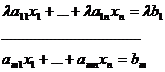 .
.
Каждое решение системы (1) есть также решение (2). Обратно: если 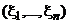 - любое решение системы (2), т.е.
- любое решение системы (2), т.е.
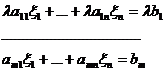 ,
,
то, умножив первое равенство на 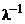 и не изменяя последующие равенства, получим равенства, показывающие, что вектор
и не изменяя последующие равенства, получим равенства, показывающие, что вектор 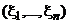 является решением системы (1). Следовательно, система (2) равносильна исходной системе (1).
является решением системы (1). Следовательно, система (2) равносильна исходной системе (1).
Т.к. отношение равносильности транзитивно, то многократное применение элементарных преобразований приводит к системе уравнений, равносильной исходной системе (1).
Также легко проверить, что однократное применение к системе (1) элементарного преобразования а) или б) приводит к системе, равносильной исходной системе (1) (проверить самостоятельно).
Следствие 1: Если к одному из уравнений системы линейных уравнений прибавить линейную комбинацию других уравнений системы, то получится система уравнений, равносильная исходной.
Следствие 2: Если исключить из системы линейных уравнений или присоединить к ней уравнение, являющееся линейной комбинацией других уравнений системы, то получится система уравнений, равносильная исходной системе.
Докажите самостоятельно.
Если в ходе преобразований в системе появятся уравнение 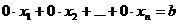 , где
, где 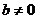 , то этому уравнению не удовлетворяет ни один вектор
, то этому уравнению не удовлетворяет ни один вектор 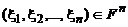 , поэтому система несовместна.
, поэтому система несовместна.
Метод Гаусса
Рассмотрим метод решения систем с действительными коэффициентами, метод последовательного исключения неизвестных, т.е. метод Гаусса.
Пусть дана произвольная система линейных уравнений
(1). 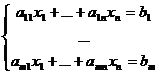
Положим для определенности, что коэффициент 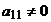 .
.
Преобразуем теперь систему (1), исключая неизвестное 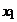 из всех уравнений, кроме первого. Для этого обе части первого уравнения умножим на
из всех уравнений, кроме первого. Для этого обе части первого уравнения умножим на 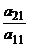 и вычтем из соответствующих частей второго уравнения, затем обе части первого уравнения, умноженные на число
и вычтем из соответствующих частей второго уравнения, затем обе части первого уравнения, умноженные на число 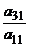 , вычтем из соответствующих частей третьего уравнения и так далее.
, вычтем из соответствующих частей третьего уравнения и так далее.
Мы придём этим путём к новой системе из 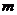 линейных уравнений с
линейных уравнений с 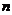 неизвестными:
неизвестными: 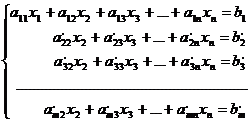 (2).
(2).
Как мы знаем, система уравнений (2) эквивалентна (1). Будем преобразовывать теперь систему (2). При этом первое уравнение мы не будем больше трогать совсем и подлежащей преобразованиям будем считать лишь часть системы (2), состоящую из всех уравнений, кроме первого. При этом мы считаем, конечно, что среди этих уравнений нет таких, все коэффициенты левых частей которых равны нулю – такие уравнения мы отбросили бы, если бы и их свободные члены были равны нулю, а в противном случае мы уже доказали бы несовместимость нашей системы. Таким образом, среди коэффициентов 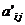 есть отличные от нуля; для определённости примем
есть отличные от нуля; для определённости примем 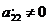 . Преобразуем теперь систему (2), вычитая из обеих частей третьего и каждого из следующих уравнений обе части второго уравнения, умноженные соответственно на числа
. Преобразуем теперь систему (2), вычитая из обеих частей третьего и каждого из следующих уравнений обе части второго уравнения, умноженные соответственно на числа 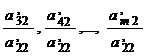 . Этим будет исключено неизвестное
. Этим будет исключено неизвестное 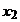 из всех уравнений, кроме первого и второго, и мы придём к следующей системе уравнений, эквивалентной системе (2), а поэтому и системе (1):
из всех уравнений, кроме первого и второго, и мы придём к следующей системе уравнений, эквивалентной системе (2), а поэтому и системе (1): 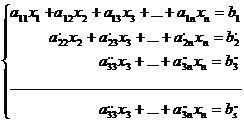 .
.
Наша система содержит 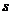 уравнений,
уравнений, 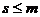 , так как некоторые уравнения могли оказаться отброшенными. Понятно, что число уравнений системы могло уменьшиться уже после исключения неизвестного
, так как некоторые уравнения могли оказаться отброшенными. Понятно, что число уравнений системы могло уменьшиться уже после исключения неизвестного 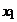 . В дальнейшем подлежит преобразованиям лишь часть полученной системы, содержащая все уравнения, кроме двух первых.
. В дальнейшем подлежит преобразованиям лишь часть полученной системы, содержащая все уравнения, кроме двух первых.
Если при выполнении преобразований мы не получили ни одного уравнения вида 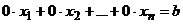 ,
, 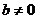 , при наличии которого система получается несовместной, то мы получим следующую систему уравнений, эквивалентную системе (1):
, при наличии которого система получается несовместной, то мы получим следующую систему уравнений, эквивалентную системе (1):
(3) 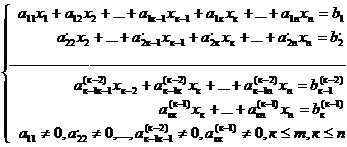 .
.
В этом случае система (1) совместна. Она будет определённой при 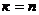 и неопределённой при
и неопределённой при 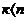 .
.
Действительно, если 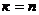 , то система (3) имеет вид:
, то система (3) имеет вид:
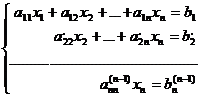 .
.
Из последнего уравнения мы получаем вполне определённое значение для неизвестного 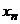 . Подставляя его в предпоследнее уравнение, мы найдём однозначное определённое значение для неизвестного
. Подставляя его в предпоследнее уравнение, мы найдём однозначное определённое значение для неизвестного 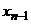 . Продолжая так далее, мы найдём однозначно значение для всех переменных. Таким образом, система (4), а значит и система (1) обладают единственным решением, т.е. совместны и определённы.
. Продолжая так далее, мы найдём однозначно значение для всех переменных. Таким образом, система (4), а значит и система (1) обладают единственным решением, т.е. совместны и определённы.
Если же 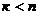 , то первые
, то первые 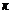 неизвестных мы возьмём за «главные» неизвестные, а оставшиеся
неизвестных мы возьмём за «главные» неизвестные, а оставшиеся  неизвестные – за «свободные». Для «свободных» неизвестных
неизвестные – за «свободные». Для «свободных» неизвестных 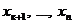 мы возьмем произвольные числовые значения, после чего, двигаясь по системе (4) снизу вверх, мы, как и выше, найдём для неизвестных
мы возьмем произвольные числовые значения, после чего, двигаясь по системе (4) снизу вверх, мы, как и выше, найдём для неизвестных 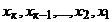 вполне определённые значения. Так как значения для свободных неизвестных можно выбрать бесконечным числом различных способов, то наша система (3) и, следовательно, система (1), будут совместными, но неопределёнными. Легко проверит, что указанным здесь методом (при всевозможных выборах значений для свободных неизвестных) будут найдены все решения системы (1).
вполне определённые значения. Так как значения для свободных неизвестных можно выбрать бесконечным числом различных способов, то наша система (3) и, следовательно, система (1), будут совместными, но неопределёнными. Легко проверит, что указанным здесь методом (при всевозможных выборах значений для свободных неизвестных) будут найдены все решения системы (1).
Замечание: При практическом решении систем линейных уравнений методом Гаусса все элементарные преобразования выполняются не над самой системой, а над её расширенной матрицей, составленной из коэффициентов и свободных членов. Для удобства столбец свободных членов отделён вертикальной чертой.
Пример : 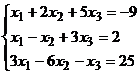 .
.
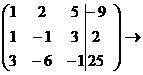
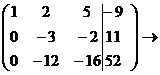
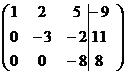 ,
, 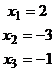
Пример : 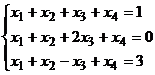 .
.
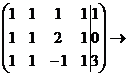
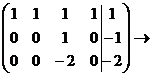
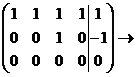
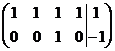
Пример: 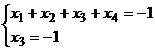 .
.
Выберем за главные переменные 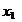 и
и 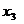 . Перепишем систему так, чтобы главные переменные остались с левой стороны, а остальные перенесем вправо. Получим систему:
. Перепишем систему так, чтобы главные переменные остались с левой стороны, а остальные перенесем вправо. Получим систему:
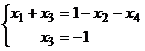 , из этой системы получаем:
, из этой системы получаем: 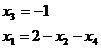 .
.
Следовательно решением системы является множество векторов вида:
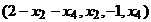 .
.
Ответ: 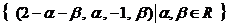
Подстановки
Определение 1: Подстановкой множества 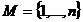 , где
, где 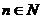 называется инъективное отображение множества М на себя.
называется инъективное отображение множества М на себя.
Другими словами, подстановкой из n элементов называется замена каждого элемента из множества М вполне определенным элементом из того же множества, причем так, что различные элементы заменяются различными элементами. Всякое отображение 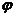 множества М на себя удобно записать в виде таблицы
множества М на себя удобно записать в виде таблицы 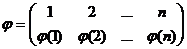 .
.
Порядок чисел в первой строке этой таблицы несуществен, его можно как угодно изменить. Однако надо следить за тем, чтобы для всякого 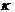 число
число 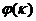 было записано непосредственно под
было записано непосредственно под 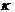 . Например:
. Например: 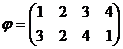 или
или 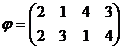 . Строки подстановки
. Строки подстановки 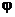 называются перестановками элементов множества
называются перестановками элементов множества 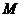 .
.
Множество всех подстановок множества М обозначим через Sn; элементы этого множества называются подстановками степени п.
Произведение 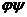 двух подстановок
двух подстановок 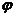 и
и 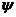 множества М определяется как композиция отображений,
множества М определяется как композиция отображений, 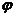 и
и 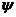 , т.е. их последовательное выполнение. Таким образом, по определению
, т.е. их последовательное выполнение. Таким образом, по определению 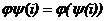 для
для 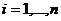 .
.
Обозначим через 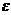 тождественное отображение М на себя:
тождественное отображение М на себя: 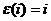 для
для 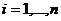 , т.е.
, т.е. 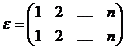 .
.
Легко видеть, что для любой подстановки 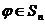
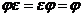 , т.е.
, т.е. 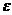 является нейтральным элементом относительно умножения.
является нейтральным элементом относительно умножения.
Если 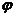 - подстановка множества М, то
- подстановка множества М, то 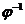 - также подстановка множества М и
- также подстановка множества М и 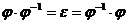 . При этом
. При этом 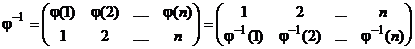 .
.
Теорема 1:Алгебра подстановок n-ой степени 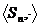 является группой.
является группой.
Докажите самостоятельно.
Определение 2: Группа всех подстановок n-ой степени 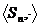 - называется симметрической группой степени
- называется симметрической группой степени 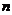 .Тождественная подстановка
.Тождественная подстановка 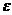 называется единичным элементом этой группы.
называется единичным элементом этой группы.
Пусть дана подстановка 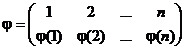 множества
множества 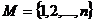 ,
, 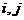 - элементы множества
- элементы множества 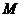 . Говорят, что числа
. Говорят, что числа 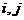 образуют инверсию в строке подстановки, если
образуют инверсию в строке подстановки, если 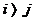 , но
, но 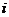 стоит в этой строке раньше
стоит в этой строке раньше 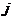 . Подстановка называется чётной,если суммарноечисло инверсий в обеих строках подстановки чётно, и нечётнойв противном случае.
. Подстановка называется чётной,если суммарноечисло инверсий в обеих строках подстановки чётно, и нечётнойв противном случае.
Так, например, в подстановке 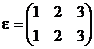 нет инверсий, она чётная, а в подстановке
нет инверсий, она чётная, а в подстановке 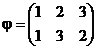 одна инверсия и она нечётная.
одна инверсия и она нечётная.
Если в любой строке подстановки любые два числа 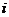 и
и 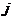 поменять местами, то её чётность измениться на противоположную. Например, поменяем в подстановке
поменять местами, то её чётность измениться на противоположную. Например, поменяем в подстановке 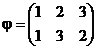 2 и 1 в нижней строке. Получим подстановку
2 и 1 в нижней строке. Получим подстановку 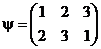 , в которой две инверсии, и она чётная.
, в которой две инверсии, и она чётная.
Рассмотрим теперь частный, но важный случай подстановки. Назовем подстановку  из чисел
из чисел 

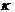 -членной циклической или
-членной циклической или 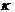 - членным циклом, если она
- членным циклом, если она 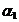 переводит в число
переводит в число 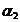 , отличное от
, отличное от 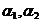 - в число
- в число 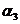 , отличное от
, отличное от 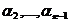 - в число
- в число 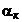 , и
, и 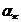 - в исходное число
- в исходное число 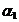
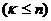 , а прочие числа ( при
, а прочие числа ( при 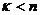 ) оставляет неизменными. Циклическая подстановка обычно обозначается символом
) оставляет неизменными. Циклическая подстановка обычно обозначается символом 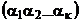 .
.
Нетрудно убедиться, что всякую подстановку из чисел  можно представить как произведение независимых циклов. Независимых в том смысле, что никакие два цикла разложения не имеют общих чисел.
можно представить как произведение независимых циклов. Независимых в том смысле, что никакие два цикла разложения не имеют общих чисел.
Для наглядности обратимся к конкретному примеру.
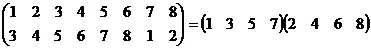

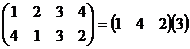 или
или 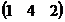
Теорема 2: Разность P между степенью n подстановки числом s независимых циклов (включая и одиночные), на которые разлагается данная подстановка, имеет ту же четность, что и данная подстановка из 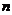 элементов. Т. е.
элементов. Т. е. 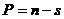
Без доказательства.
Примеры: 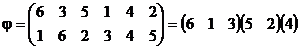 ,
, 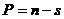 = 6 – 3 = 3 ; значит подстановка
= 6 – 3 = 3 ; значит подстановка 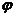 - нечетна.
- нечетна.
Обозначим через 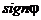 знак подстановки
знак подстановки 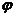 , тогда
, тогда
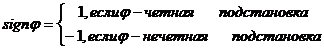 .
.
Можно сказать, что 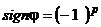 , где
, где 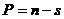 , или
, или 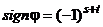 , где
, где 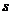 и
и 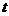 - числа инверсий в верхней и нижней строках подстановки
- числа инверсий в верхней и нижней строках подстановки 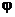 .
.
Теорема 3:Произведение двух (или четного числа) подстановок одинаковой чет
