Общая схема исследования функции
I этап – асимптотическое исследование фун-и
1. Область определения
2. Точки разрыва II рода, вертикальные асимптоты
3. f(0), если легко
4. Четность, нечетность
5. Невертикальные асимптоты.
II этап – исследование фун-и на монотонность.
1. f’(x), f’(x)=0
2. Критическими точками делим обл.опред. на интервалы монотонности и результаты оформляем в таблицу.
| x | - 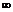 ;х1 ;х1 | х1 | х1, х2 | x2 | x2,+¥ |
| f’(x) | + | max | - | min | + |
| f(x) | 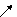 | f(x1) | 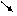 | f(x2) | 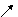 |
III этап – исследование фун-и на выпуклость.
1. Находим вторую производную f’’(x), f’’(x)=0,
точки х1, х2, подозрительные на перегиб.
2. Разбиваем D(y) этими точками.
3. Оформляем результат в таблицу.
| x | - 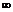 ;х1 ;х1 | х1 | х1, х2 | x2 | x2,+¥ |
| f’’(x) | + | max | - | min | + |
| f(x) | È | f(x1) | Ç | f(x2) | È |
IV. Строим график функции.
Формулы
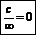
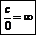
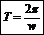
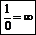 хn=n!
хn=n!
0!=1
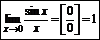 |
Первый замечательный предел:
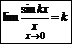 Следствия:
Следствия:
Þ1. 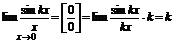
Þ2. 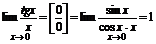
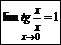
Þ3.
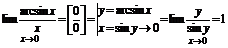
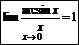
Второй замечательный предел:
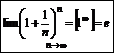 - n – для натуральных чисел
- n – для натуральных чисел
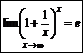 - х – для любых чисел
- х – для любых чисел
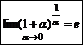 -
- 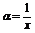
Следствия:
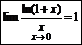
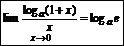 Þ1
Þ1
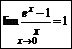
Þ2
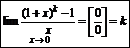 |
Þ3
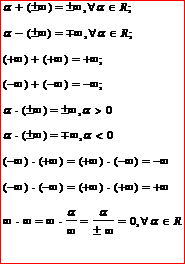 Операции над символами бесконечности:
Операции над символами бесконечности:
Таблица эквивалентных б.м.:
sinx~x 7. ax – 1~xlna,a>0,a¹1 sinkx~kx 8. ex-1~x arcsinx~x 9. ln(1+x) ~x tgx~x 10. (1+x)k – 1 ~kx arctgx~x 11. 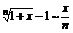 loga(1+х) ~(logae)(x) 12. loga(1+х) ~(logae)(x) 12. 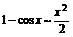 |
Таблица производных:
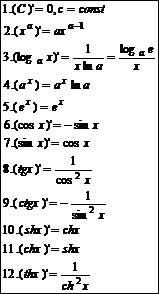 | 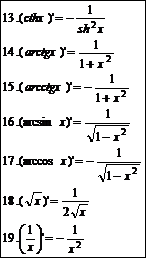 | ||
Свойства производных:
1. (u(x)±v(x))’=v’(x)±v’(x)
2. (u(x)  v(x))’=u’(x)*v(x)+v’(x)*u(x)
v(x))’=u’(x)*v(x)+v’(x)*u(x)
3. 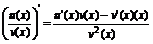
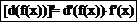 производная сложной функции:
производная сложной функции:
Производная функции, заданной параметрически:
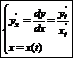
Формула Тейлора:
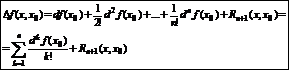
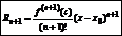 |
Формула Лагранжа:
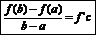 |
Теорема Лагранжа:
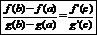 |
Теорема Коши:
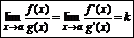 |
Правило Лапиталя:
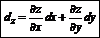 |
Полный дифференциал:
Полный дифференциал – сумма частных дифференциалов:
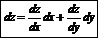 |
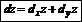
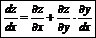 | 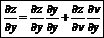 |
Дифференцирование сложных функций:
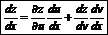
Дифференцирование неявных функций:
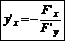 в точке М0
в точке М0
Производные дифференциала высшего порядка:
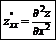 | 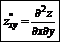 | 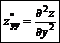 | |||
повторные смешанные
производные производные
Если смешанные производные непрерывны, они всегда равны.
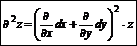
производная по направлению: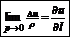
43. Содержание
1. Множества, операции над ними. 3
2.Числовые множества, их границы. 4
3. Операции над символами бесконечности. 5
4. Понятие функции. 7
5. Частные классы отображений. 8
6.Класс основных элементарных функций. 10
7. Суперпозиция (композиция отображений) 11
8. Системы окрестностей. 11
9. Предел последовательности (определение Коши) 12
10.Определение предела функции на языке последовательностей (определение Гейне). 13
11. Теоремы о пределах. 14
12. Раскрытие неопределенности. 14
13. Непрерывность функций. 15
14. Классификация точек разрыва. 17
15. Замечательные пределы. 18
16. Второй замечательный предел и его свойства. 19
18. Главная часть б.м. 22
19. Сравнение б.м. 22
20. Сравнение б.б. 23
21. Свойства эквивалентных бесконечно малых функций. 24
22. Таблица эквивалентных б.м. 25
23. Понятие производной. 26
24. Физический, геометрический и экономический смысл производной. 26
25. Таблица производных. 28
26. Производная сложных функций. 30
27. Производная высшего порядка. 31
28. Дифференцирование функций, заданных неявно. 31
29. Дифференцирование параметрически заданных функций. 31
30. Производная по направлению. 32
31. Уравнение касательной плоскости и нормали к поверхности. 32
32. Дифференциал функции. 34
33. Формула Тейлора. 35
34. Формула Лагранжа. 35
35. Формула Маклорена. 35
36. Основные теоремы дифференциального исчисления. 35
37. Условия постоянства функции. 38
38. Достаточные условия экстремума. 38
39. Выпуклость графика функции. 39
40. Асимптоты графикафункции. 40
41. Общая схема исследования функции. 41
42. Формулы. 42
