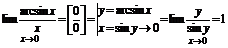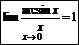Определение предела функции на языке последовательностей (определение Гейне).

Говорят, что точка А – предел функции f(x)

, если для всякой последовательности точек {x_n} (x_n¹x₀) из области определения функции, сходящейся к х₀, последовательность {f(x_n)} значений функции имеет пределом точку А.

Теоремы о пределах.

1. Если предел существует, то он единственный, если пределов больше 1, то предела не существует.

2. Если существует предел Xn=a, то ограничена в окрестности точки а. (обратное нет!)

3. Всякая монотонная ограниченная последовательность имеет предел.

4. Пусть 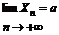, , 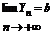тогда А – предел суммы:

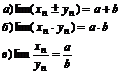
Предел вычисляется, если y_n®0, предел =0, а y_n¹0.

Раскрытие неопределенности.

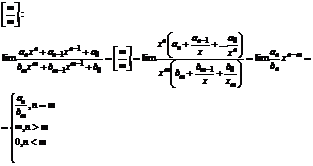
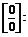
Чтобы решить пример с данной неопределенностью, необходимо максимально упростить выражение, сократить какие-либо переменные, и подставить число из предела.

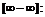
Чтобы решить пример с этой неопределенностью, мы упрощаем выражение и затем подставляем 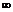вместо неизвестной переменной. По определенным формулам ищем значение.

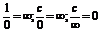
Непрерывность функций.

Непрерывной называется функция f(x) в точке x₀, если предел f(x)=f(x₀) при х®х₀.

lim f(x)=f(x₀)Ûlim f(x)=lim f(x)=f(x₀)

x®x₀ x®x₀

lim (x₀-0)=lim f(x) - предел слева

lim (x₀+0)=lim f(x) – предел справа.

Непрерывной является такая функция, у которой предел слева = пределу справа.
Теорема1. Для того, чтобы функция была непрерывной в точке х₀ Û чтобы она была непрерывна слева и справа в этой точке.

Теорема2. Если функции f и t непрерывны в точке х₀, то и функции f+t, f*t, f/t (t(x₀)¹0) тоже будут непрерывны в этой точке.

Теорема3. Для того, чтобы функция y = f(x) была непрерывна в точке х₀, Û чтобы все ее координатные функции были непрерывны в х₀.

Теорема4. Пусть функция f непрерывна в точке x₀ и t непрерывна в точке y₀. Тогда их суперпозиция (сложная функция) f 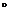t=f(t) также непрерывна в точке х₀.

Теорема5. Все элементарные функции вещественного переменного непрерывны в области определения.

Теорема6. Пусть скалярная функция f скалярного переменного задана на отрезке [a,b] и f(a)=A, f(b)=B, A¹B. Если функция f непрерывна на [a,b], то для любого С, лежащего между А и В, существует точка с Î[a,b] такая, что f(c)=C.

Теорема7. Если функция y=f(x) непрерывна в замкнутой области Х и в некоторых точках, принадлежащих этой области, принимает определенные значения, неравные между собой, то для любого числа С, заключенного между этими значениями, существует точка х₂ такая, что f(x₂)=C.

Теорема 8 (I теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном в R_n множестве Х функция y=f(x) ограничена на этом множестве.

Теорема9 (II теорема Вейерштрасса). Всякая непрерывная на замкнутом ограниченном множестве в R_n функция f(x) принимает в нем наибольшее и наименьшее значения.

Степенная функция – функция вида f(x) = x^a,a ÎR

Показательная функция – функция вида f(x) = a^x, а¹1, а>0. а – const, x – переменная.

Степенно-показательная функция – функция вида f(x)=u(x)^v(x).

Точка разрыва функции f(x) - точка х₀ в которой нарушается непрерывность, а поэтому в этой точке нарушается одно из равенств.

Классификация точек разрыва

Существует 3 нарушения:

1. Устранимый разрыв.

Устранимым разрывом называется точка х₀, если конечный предел слева равен конечному пределу справа и ¹ f(x₀).

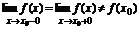
2. Разрыв I рода (неустранимый).

Точкой разрыва I рода называется точка х₀, если конечные пределы 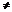(односторонние).

.

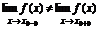3. Разрыв II рода

Точка разрыва II рода – точка x₀, при которой хотя бы один из односторонних пределов = 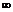или не существует.

Замечательные пределы.

Первый замечательный предел и его следствия.

- Первый замечательный предел.

Следствия:

Þ1.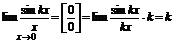

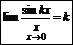
Þ2.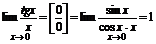

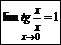
Þ3.