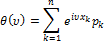Функция распределения дискретной случайной величины

Для каждого значения 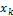дискретной случайной величины 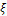задана вероятность:

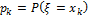
Тогда функция распределения:

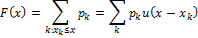
Где 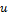— функция единичного скачка:

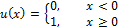
Плотность распределения вероятностей

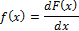
Где 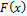— дифференцируемая функция распределения случайной величины .

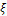Свойства:

1.

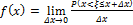
2.

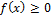
3.

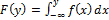
4.

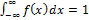
5.

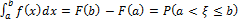
Плотность распределения вероятностей дискретной случайной величины

Для каждого значения 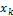дискретной случайной величины 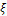задана вероятность:

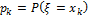
Тогда плотность вероятности:

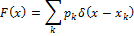
Где 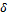— дельта-функция.

Примеры распределения случайной величины

1. Равномерное.

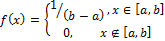
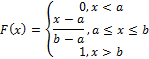
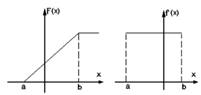
2. Нормальное (гауссовое).

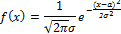
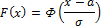
Где 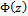— функция Лапласа.

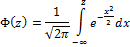
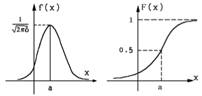
3. Коши.

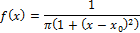
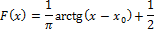
4. Экспоненциальное распределение.

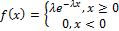
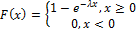
Математическое ожиданиедискретной случайной величины

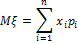
Где 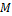— оператор математического ожидания, 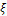дискретнаяслучайная величина, 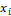— одно из 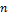возможных значений случайной величины с вероятностью .

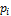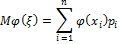
Где 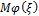— математическое ожидание функции.

Математическое ожидание непрерывной случайной величины

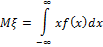
Где 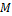— оператор математического ожидания, 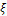случайная величина с плотностью распределения .

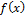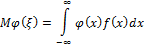
Где 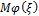— математическое ожидание функции.

Свойства математического ожидания

1.

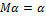
2.

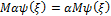
3. 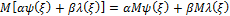. Оператор математического ожидания линейный.

Примеры математического ожидания

1. Равномерное распределение.

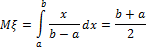
2. Нормальное распределение.

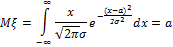
3. Схема Бернулли.

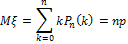
Дисперсия случайной величины

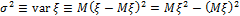
Где 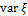(иногда 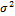) — дисперсия (среднее значение отклонения от математического ожидания) случайной величины 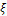, 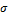— среднеквадратичное отклонение, 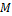— оператор математического ожидания.

Для дискретной случайной величины:

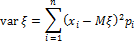
Где 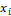— одно из 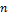возможных значений случайной величины с вероятностью .

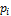Для непрерывной случайной величины:

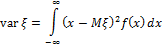
Где 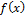— плотность распределения .

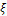Примеры дисперсии

1. Нормальное распределение.

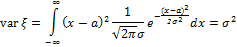
2. Экспоненциальное распределение.

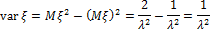
3. Схема Бернулли.

Моменты случайных величин

Начальный момент k-го порядка:

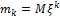
Для непрерывной величины:

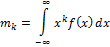
Для дискретной величины:

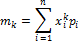
Центральный момент k-го порядка:

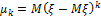
Для непрерывной случайной величины:

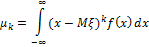
Для дискретной случайной величины:

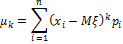
Неравенство Чебышева

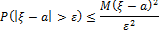
Где 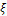— случайная величина, 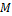— оператор математического ожидания, 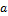и 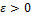— произвольные параметры.

Коэффициент асимметрии

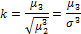
Где 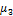— центральный момент третьего порядка, 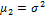— центральный момент второго порядка (дисперсия).

Коэффициент эксцесса

Характеризует степень сглаженности вершины плотности вероятности.

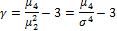
Где 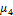— центральный момент четвёртого порядка, 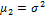— центральный момент второго порядка (дисперсия).

Чем больше 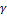, тем острее вершина, у нормального распределения .

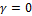Среднеквадратическая ошибка

Пусть 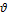(буква — тэта) — неизвестный параметр системы, который измеряют. Результат измерения есть случайная величина 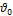(оценка параметра ).

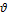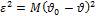
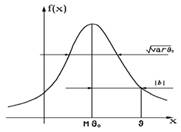
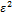— среднеквадратичная ошибка (похоже на дисперсию, но не оно, потому что 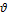— не математическое ожидание).

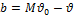
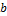— смещение оценки .

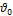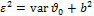
Где 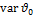дисперсия величины .

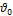Характеристическая функция

Характеристическая функция случайной величины :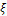

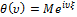
Для непрерывной случайной величины с плотностью вероятности :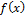

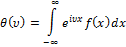
Это выражение так же называется преобразованием Фурье. Возможно обратное преобразование:

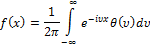
Для дискретной случайной величины со значениями 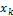и с соответствующими вероятностями :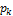