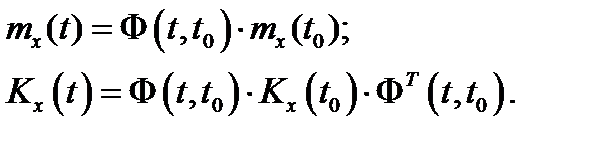Плотность распределения вероятностей обладает следующими свойствами

Условная плотность

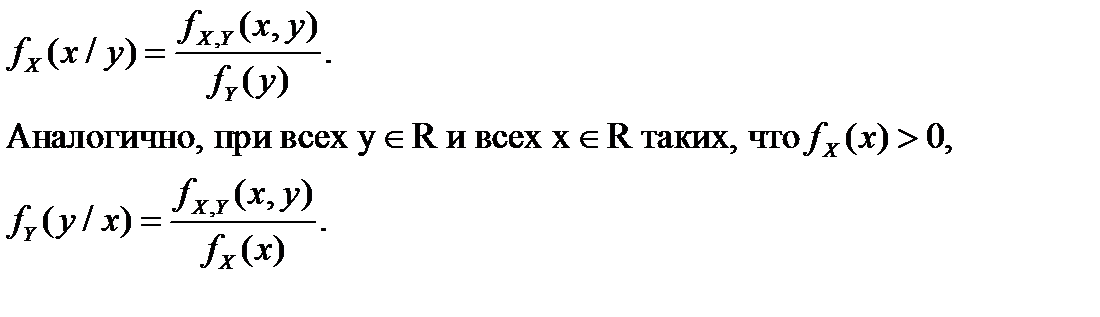
Условие независимости

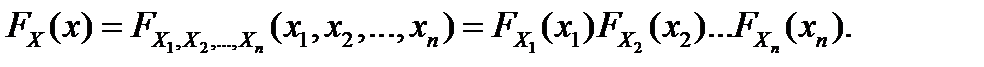
Для непрерывных СВ

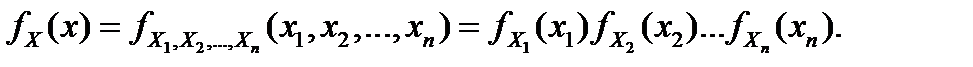
Для дискретных СВ

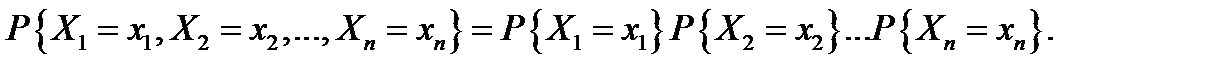
Корреляционный момент

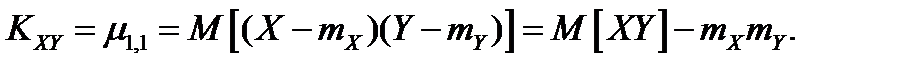
Нормированная ковариация 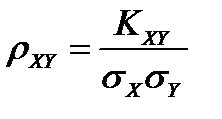называется коэффициентом корреляции двух случайных компонент Xи Yслучайного вектора.

Коэффициент корреляции удовлетворяет условию 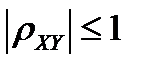и определяет степень линейной зависимости между XиY. Случайные величины, для которых 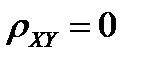, называются некоррелированными. Из независимости случайных величин Xи Y следует их некоррелированность (обратное, в общем случае, неверно).

Ковариационной матрицейn – мерного случайного вектора 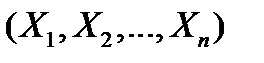называется симметрическая действительная матрица, элементы которой представляют собой корреляционные моменты (ковариации) соответствующих пар компонент:

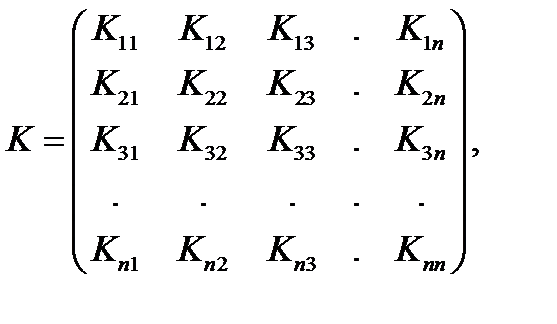
где

Корреляционной матрицейn – мерного случайного вектора называется нормированная ковариационная матрица

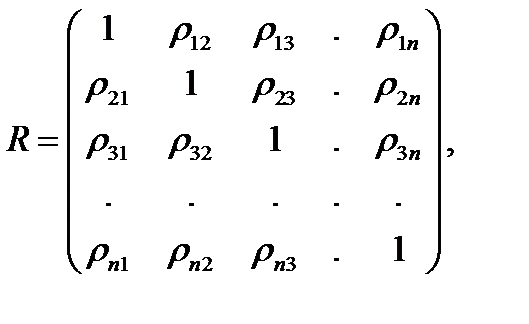
где 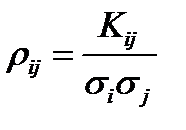- коэффициент корреляции i – й и j–й компонент.

Функции случайных величин

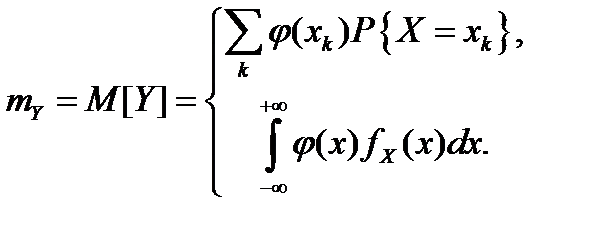
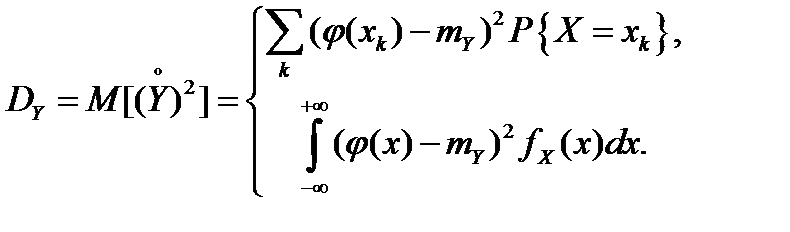
Если существуют соответствующие моменты, то справедливы следующие свойства математического ожидания и дисперсии для любых случайных величин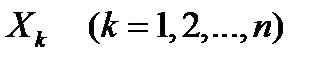

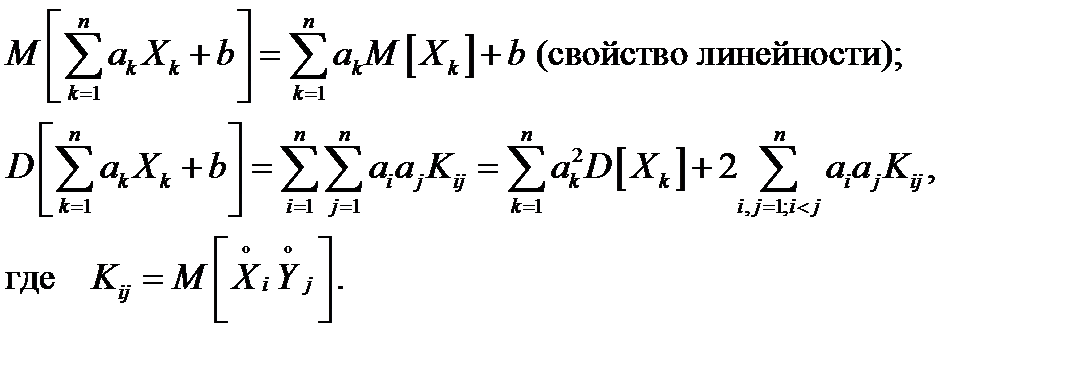
СЛУЧАЙНЫЕ ПРОЦЕССЫ

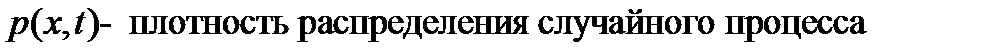
Марковский СП

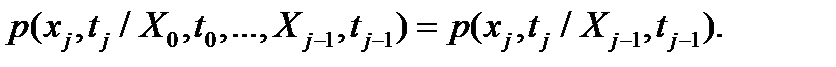
Математическое ожидание

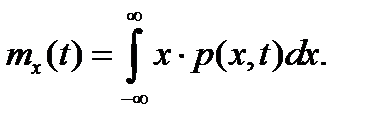
Корреляционная функция

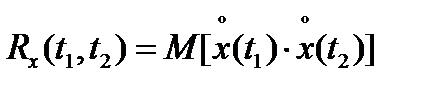
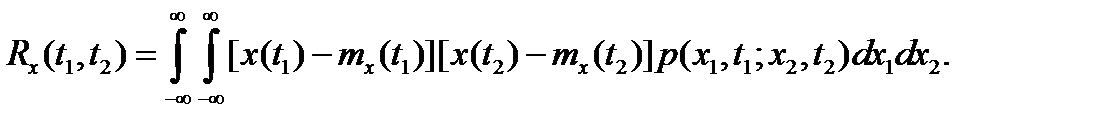
Дисперсия

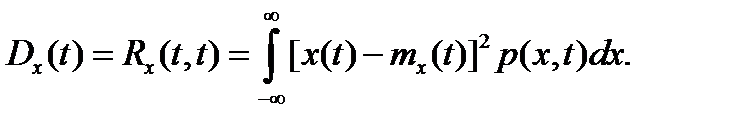
Матричная корреляционная функция

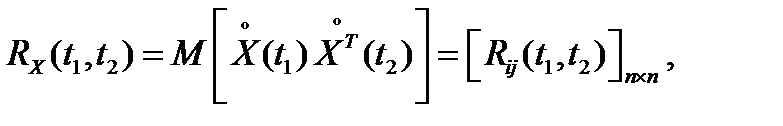
где 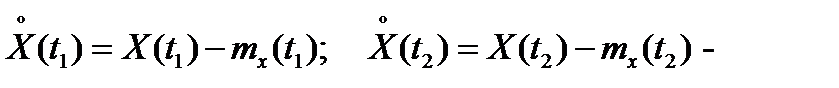центрированные случайные векторы. Диагональные элементы 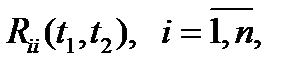матричной корреляционной функции называются автокорреляционными функциями соответствующих компонент векторного случайного процесса 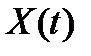, а внедиагональные элементы 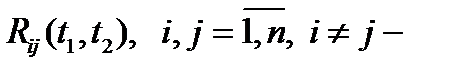взаимными корреляционными функциями компонент 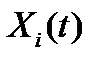и .

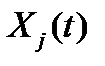Белый шум

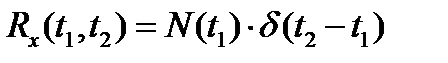
Стационарный в широком смысле случайный процесс

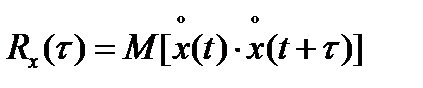
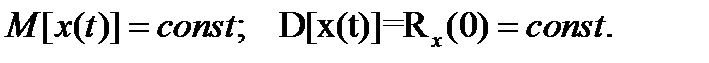
Спектральная плотность

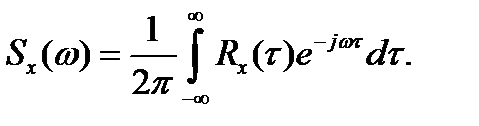
Корреляционная функция и дисперсия

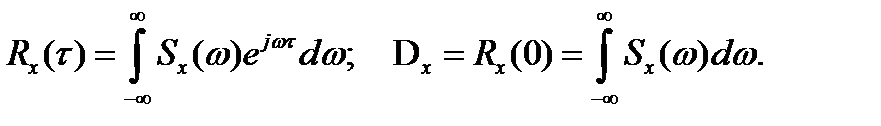
Спектральная плотность стационарного белого шума

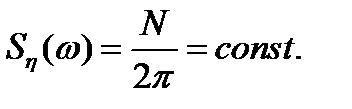
ЧАСТОТНЫЙ МЕТОД

Связь между спектральными плотностями на входе и выходе линейной стационарной системы

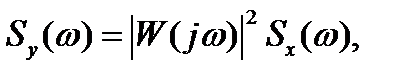
где 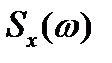- спектральная плотность входного сигнала;

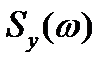- спектральная плотность выходного сигнала;

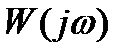- частотная передаточная функция системы.

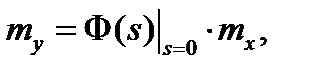
где 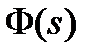передаточная функция замкнутой системы;

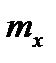- математическое ожидание входного сигнала;

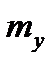- математическое ожидание сигнала на выходе системы.

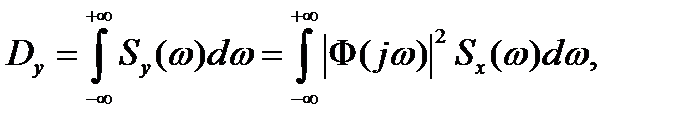
где 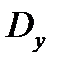- дисперсия сигнала на выходе системы.

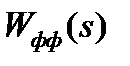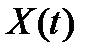Схема формирующего фильтра

Формирующий фильтр

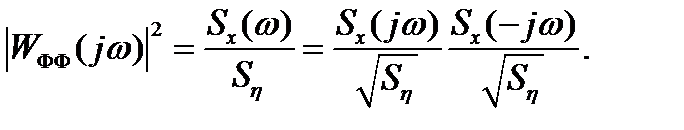
МЕТОД СТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ (МЕТОД МОНТЕ-КАРЛО)

Оценки по множеству реализаций

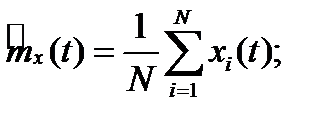
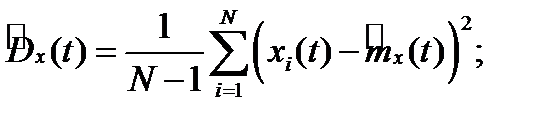
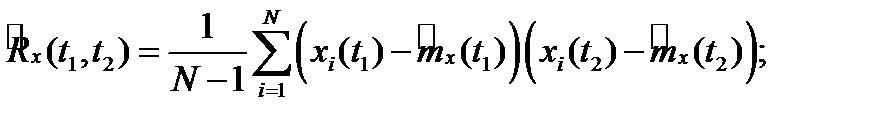
Для стационарного процесса

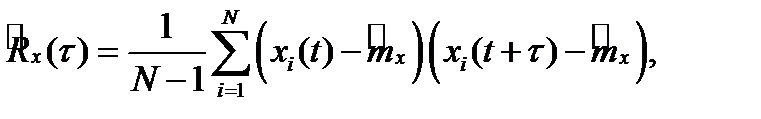
где 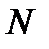- число реализаций случайного процесса .

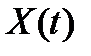Оценки по одной реализации для эргодического процесса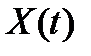

Вычисление оценок по непрерывной реализации процесса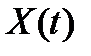

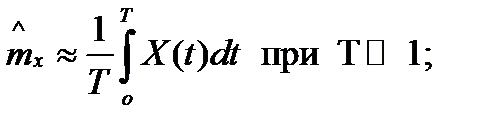
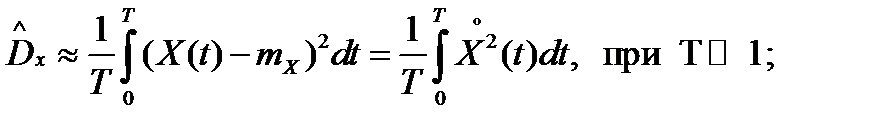
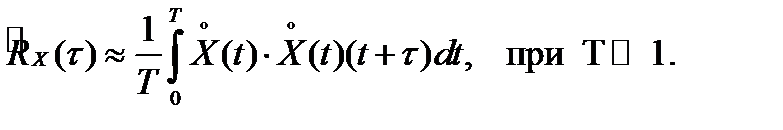
Вычисление оценок по значениям процесса 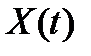в дискретные моменты времени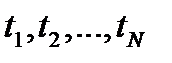

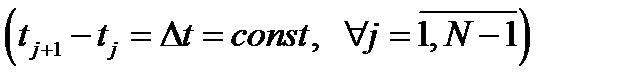
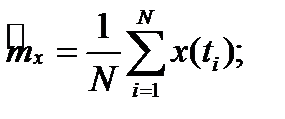
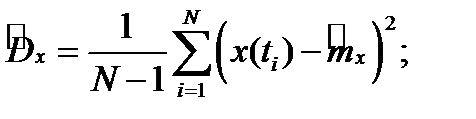
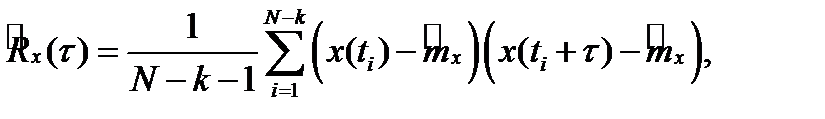
где величина 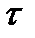меняется от 0 до интервала корреляции 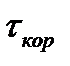и кратна ;

.

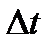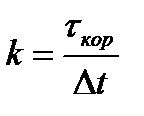МЕТОД ПЕРЕХОДНОЙ МАТРИЦЫ

Линеаризованное уравнение динамики

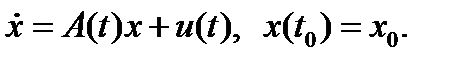
Линейное соотношение для измерений

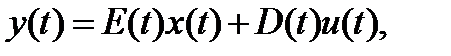
Переходная матрица 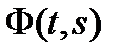удовлетворяет уравнению

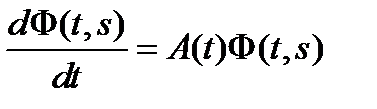
При нулевом входном воздействии – u=0 математическое ожидание 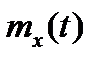и ковариационая функция 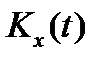вектора состояния определяются из соотношений