Корреляционный анализ. Регрессионный анализ.
89. Что понимается под корреляцией?
a) это зависимость между неслучайными величинами
b) это зависимость между случайными величинами
c) это функциональная зависимость
90. Существует ли и какого типа корреляция между ростом человека и его весом?
a) существует; отрицательная
b) существует; положительная
c) не существует
91. Корреляция между двумя случайными величинами является положительной, если:
a) с возрастанием одной величины другая уменьшается
b) с возрастанием одной величины другая тоже возрастает
c) с возрастанием одной величины другая не меняется
92. Корреляция между двумя случайными величинами является отрицательной, если:
a) с возрастанием одной величины другая уменьшается
b) с возрастанием одной величины другая тоже возрастает
c) с возрастанием одной величины другая не меняется
93. Корреляция между двумя случайными величинами отсутствует, если:
a) с возрастанием одной величины другая уменьшается
b) с возрастанием одной величины другая тоже возрастает
c) с изменением одной величины нельзя заметить тенденцию изменения другой
94. Качественно наличие корреляции устанавливается путём:
a) построения гистограммы
b) построения корреляционного поля
c) построения полигона распределений
95. По степени (силе связи) корреляция может быть:
a) пропорциональная, непропорциональная, обратно пропорциональная
b) неявная, явная, очевидная
c) сильная, средняя, слабая
96. Для определения степени корреляции (силы связи) необходимо вычислить:
a) доверительные интервалы в сравниваемых выборках
b) коэффициент корреляции
c) выборочные характеристики сравниваемых выборок
97. Какое из утверждений является правильным?
a) коэффициент корреляции может быть вычислен для любых законов распределения случайных величин и для всех видов корреляции
b) коэффициент корреляции может быть вычислен только при нормальном законе распределения и линейной корреляции
c) коэффициент корреляции может быть вычислен при любых законах распределения случайных величин, но только для линейных корреляций
98. Значение коэффициента корреляции может изменяться в пределах
a) от 0 до +1
b) от -1 до + 1
c) от - ∞ до + ∞
99. Если значение коэффициента корреляции равно ± 1, то
a) зависимость между случайными величинами является функциональной зависимостью
b) корреляционная зависимость является слабо выраженной
c) корреляционная зависимость отсутствует
100. Задачей регрессионного анализа является:
a) подтверждение наличия корреляционной связи между случайными величинами
b) нахождение уравнения, описывающего корреляцию
c) разбиение статистического ряда на классовые интервалы
101. Проводить регрессионный анализ имеет смысл, если:
a) корреляция слабая или отсутствует
b) корреляция сильная или хотя бы средняя
c) регрессионный анализ имеет смысл проводить всегда
102. 
На диаграмме изображено корреляционное поле. Что можно сказать о корреляции между Y и Х?
a) отсутствует
b) есть, положительная, линейная
c) есть, отрицательная, линейная
d) есть, отрицательная, нелинейная
e) есть, положительная, нелинейная
103. На диаграмме изображено корреляционное поле. Что можно сказать о корреляции между Y и Х?
a) отсутствует
b) есть, положительная, линейная
c) есть, отрицательная, линейная
d) есть, отрицательная, нелинейная
e) есть, положительная, нелинейная
104. На диаграмме изображено корреляционное поле. Что можно сказать о корреляции между Y и Х?
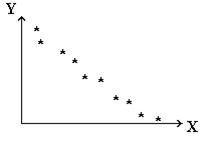
a) отсутствует
b) есть, положительная, линейная
c) есть, отрицательная, линейная
d) есть, отрицательная, нелинейная
e) есть, положительная, нелинейная
105. 
На диаграмме изображено корреляционное поле. Что можно сказать о корреляции между Y и Х?
a) отсутствует
b) есть, положительная, линейная
c) есть, отрицательная, линейная
d) есть, отрицательная, нелинейная
e) есть, положительная, нелинейная
106. 
На диаграмме изображено корреляционное поле. Что можно сказать о корреляции между Y и Х?
a) отсутствует
b) есть, положительная, линейная
c) есть, отрицательная, линейная
d) есть, отрицательная, нелинейная
e) есть, положительная, нелинейная