Электромагнитные волны на границе раздела 2-х диэлектриков. Нормальное падение.
Пусть есть граница раздела 2-х сред.
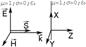
Пусть линия раздела плоская или взята маленькая плоская площадка.
Рассмотри случай, когда вектор Поинтинга перпендикулярен поверхности раздела.
Пусть обе эти диспергирующие среды изотропны.
Пусть оси 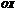 и
и 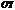 параллельны соответственно
параллельны соответственно  и
и 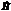 (этого можно добиться выбором системы координат).
(этого можно добиться выбором системы координат).
Тогда часть волны отразиться, а часть пройдёт сквозь границу раздела.
 - отражённая волна.
- отражённая волна.
 - прошедшая волна.
- прошедшая волна.
Найдём соотношения между характеристиками этих 3-х волн.
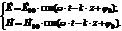
Где 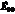 и
и 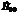 - амплитуды составляющих начальной волны. Тогда
- амплитуды составляющих начальной волны. Тогда
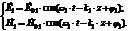
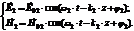
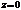 - граница раздела фаз.
- граница раздела фаз. 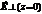 - т.е. вектор
- т.е. вектор  непрерывен, т.к. есть только тангенсальная составляющая. Т.е.:
непрерывен, т.к. есть только тангенсальная составляющая. Т.е.:
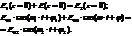 Откуда, в силу того, что это равенство справедливо во все моменты времени, следует:
Откуда, в силу того, что это равенство справедливо во все моменты времени, следует:
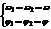 ,
,
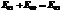 .
.
 Мы записали граничные условия для нормального падения электромагнитной волны на границу раздела двух диэлектриков.
Мы записали граничные условия для нормального падения электромагнитной волны на границу раздела двух диэлектриков. 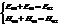 . Также мы установили, что частота падающей и отраженной волны одинаковы. Теперь найдем какая часть волны отражается, а какая проходит.
. Также мы установили, что частота падающей и отраженной волны одинаковы. Теперь найдем какая часть волны отражается, а какая проходит.
Если в среде распространяется волна, то выполняется соотношение 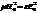 . Мы будем работать в системе единиц СГСЕ. Рассмотрим случай, когда магнитная восприимчивость
. Мы будем работать в системе единиц СГСЕ. Рассмотрим случай, когда магнитная восприимчивость 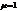 . Тогда для падающей, отраженной и прошедшей волн можно записать следующие равенства
. Тогда для падающей, отраженной и прошедшей волн можно записать следующие равенства 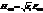 ,
, 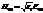 ,
, 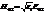 . Введем обозначения
. Введем обозначения 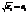 ,
, 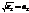 .
.
Числа 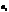 и
и 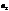 называются показатели преломления среды.
называются показатели преломления среды.
Граничные условия теперь запишутся так: 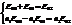 . Теперь выразим
. Теперь выразим 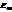 и
и 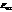 через
через 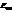 :
:
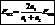 ,
, 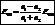 .
.
Видим, что 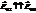 при любых соотношениях показателей преломления.
при любых соотношениях показателей преломления.
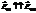 - при
- при 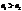
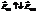 - при
- при 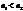 - отраженная волна имеет начальную фазу
- отраженная волна имеет начальную фазу  .
.
Т.е. при отражении от зеркала волна приобретает сдвиг фаз равный  , а если светить фонариком из воды, никакого сдвига фаз нет.
, а если светить фонариком из воды, никакого сдвига фаз нет.
Рассмотрим 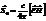 - вектор потока энергии (вектор Пойнтинга).
- вектор потока энергии (вектор Пойнтинга).
Мы будем видеть усредненный вектор Пойнтинга, т.к. период колебаний и время измерения различаются на много порядков 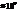 .
. 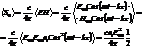
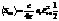 ,
, 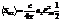 .
.
Коэффициент отражения 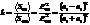 .
.
Коэффициент прохождения 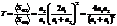 .
.
Эти результаты мы получили исходя только из граничных условий.
В общем случае фазовая скорость электромагнитной волны выражается следующим образом: 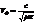 . Мы рассматриваем случай, когда магнитная восприимчивость
. Мы рассматриваем случай, когда магнитная восприимчивость 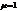 , тогда
, тогда 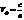 . Фазовая скорость электромагнитной волны в среде с показателем преломления
. Фазовая скорость электромагнитной волны в среде с показателем преломления  меньше фазовой скорости электромагнитной волны в вакууме в
меньше фазовой скорости электромагнитной волны в вакууме в  раз.
раз.
Падающая и отраженная волны имеют одинаковые фазовые скорости, а падающая и прошедшая – разные.
Рассмотрим уравнения падающей и прошедшей волн: 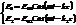 волновые числа у этих волн различны, т.к. они распространяются в средах с разными показателями преломления
волновые числа у этих волн различны, т.к. они распространяются в средах с разными показателями преломления 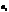 и
и 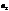 :
: 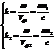 .
.
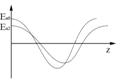
Построим осциллограмму этих волн в точке 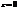 .
.
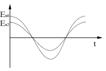
А теперь «сфотографируем» эти волны в момент времени 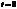 :
: 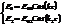 .
.
Колебания происходят с одинаковой частотой, но т.к. скорости распространения разные получаются разные длины волн.
